人教版七年级数学下册7.1.2.2《平面直角坐标系作图》课件(共32张PPT)
文档属性
| 名称 | 人教版七年级数学下册7.1.2.2《平面直角坐标系作图》课件(共32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 18:47:53 | ||
图片预览





文档简介
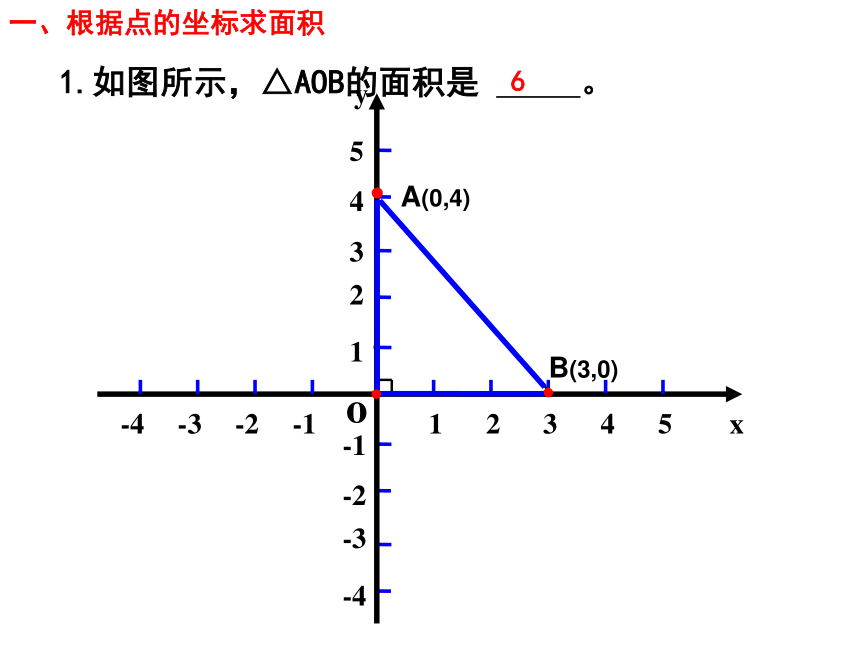
1.如图所示,△AOB的面积是 。
6
B(3,0)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
? A(0,4)
?
一、根据点的坐标求面积
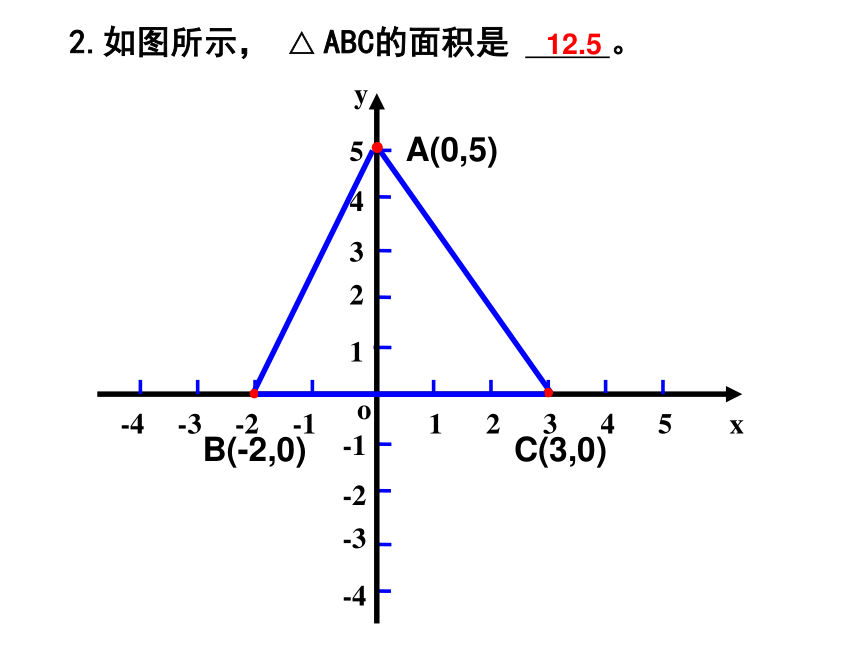
2.如图所示, △ ABC的面积是 。
C(3,0)
B(-2,0)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
?
? A(0,5)
12.5
B(5,0)
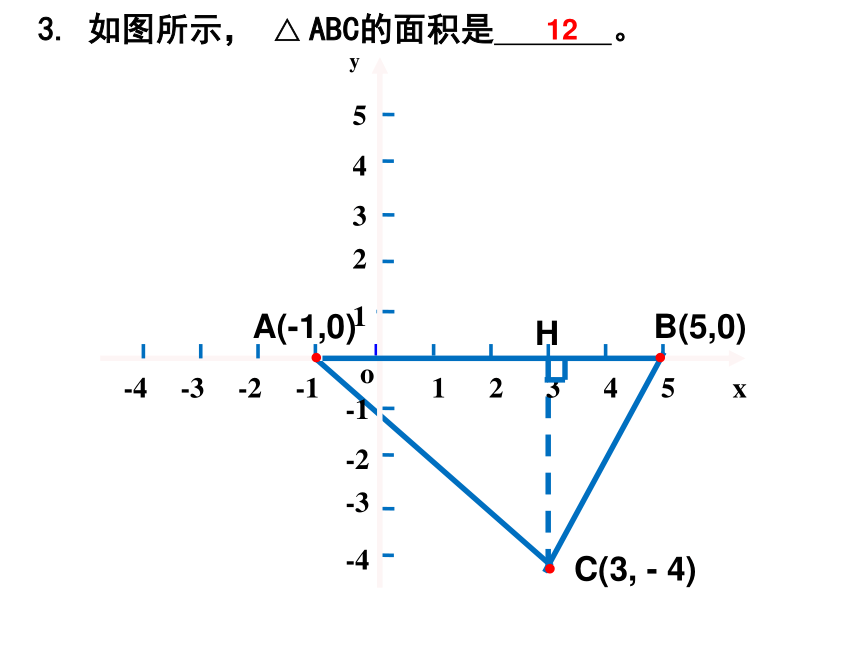
3. 如图所示, △ ABC的面积是 。
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
? C(3, - 4)
H
A(-1,0)
?
?
12
y
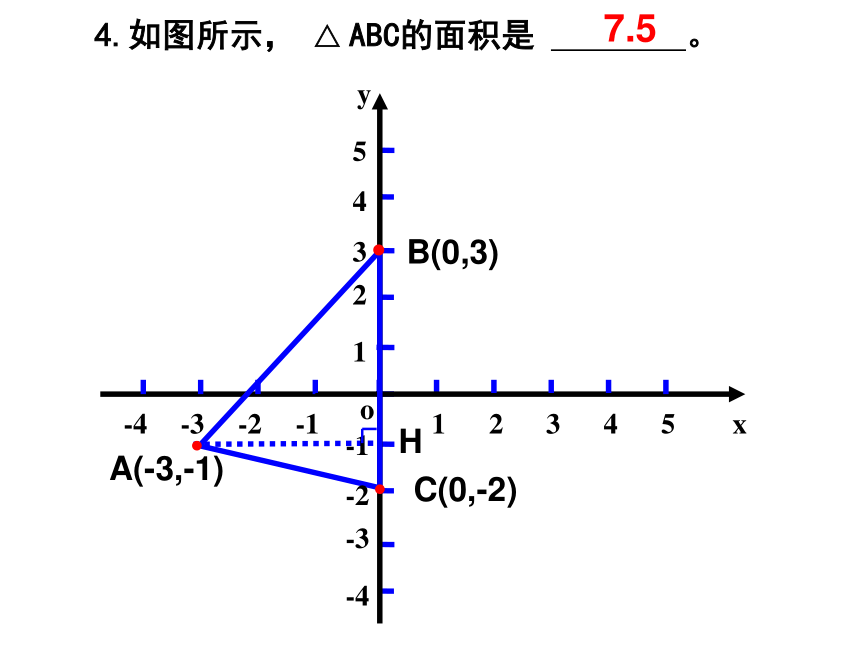
4.如图所示, △ ABC的面积是 。
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
H
7.5
? C(0,-2)
A(-3,-1)
?
? B(0,3)
选取在坐标轴上的边作为三角形的底。
5.已知:A(3,5),B(1,2),C(5,2),
则△ ABC的面积 。
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
6
?
?
?
B(1,2)
A(3,5)
C(5,2)
H
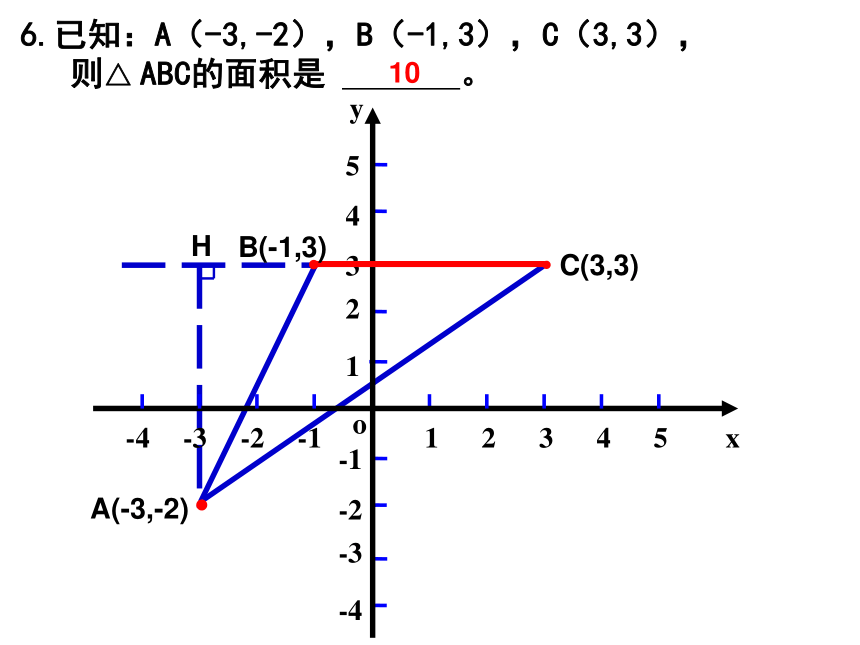
6.已知:A(-3,-2),B(-1,3),C(3,3),
则△ ABC的面积是 。
o
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
x
y
A(-3,-2) ?
?
? C(3,3)
B(-1,3)
10
H
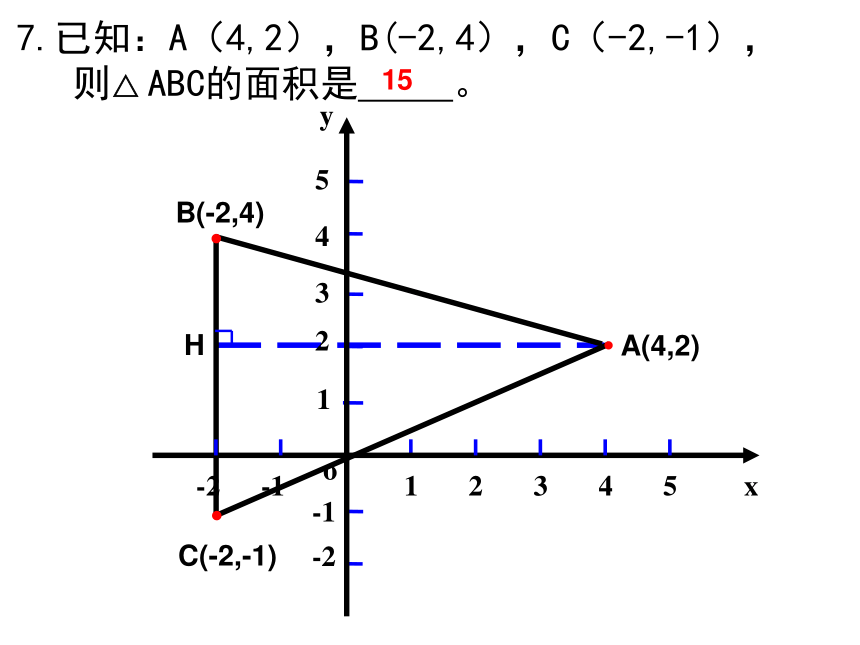
7.已知:A(4,2),B(-2,4),C(-2,-1),
则△ ABC的面积是 。
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
? A(4,2)
?
?
C(-2,-1)
15
H
B(-2,4)
选取平行于坐标轴的边作为三角形的底。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
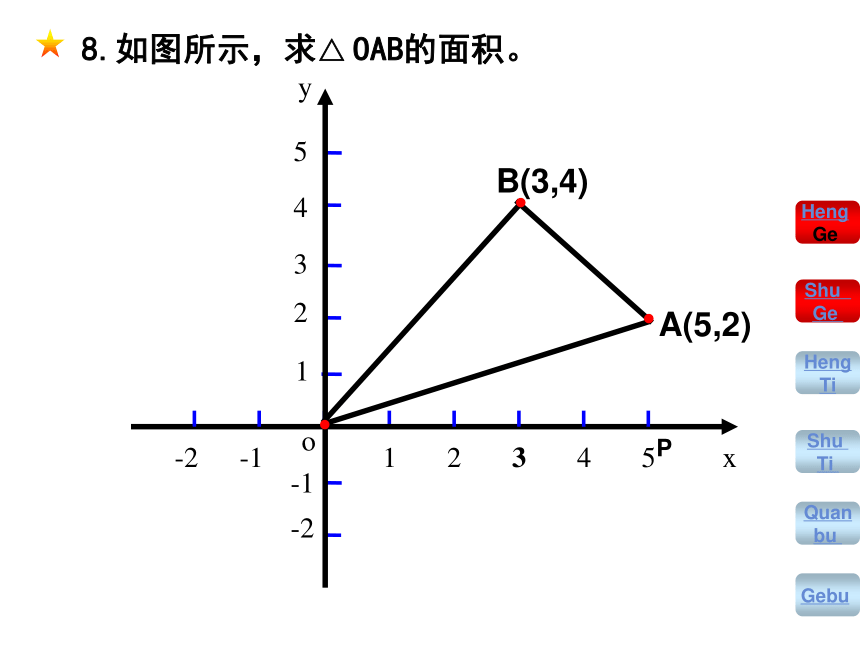
8.如图所示,求△ OAB的面积。
Heng
Ti
Shu
Ti
Heng
Ge
Shu
Ge
P
Quan
bu
Gebu
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
利用现在所学过的知识你能确定M点的坐标吗?
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
N
M
S=S梯形OAMN– S1 –S2
s1
s2
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
S=S梯形OPMB– S1 –S2
P
s1
s2
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
N
M
S=S长方形OPMN– S1 – S2 –S3
P
s1
s2
s3
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
S=S △ BOM+ S梯形BMPA– S △ AOP
P
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
8.如图所示,求△ OAB的面积。
P
返回
Shu
ge
Heng
ge
Ge
bu
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
9.如图所示,则四边形AOBC的面积是 。
13
heng
bu
Bu
chang
xie
ge
Yan
chang
H S
ge
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
N
M
s1
s2
S=S长方形NOBM– S1 –S2
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
N
s1
S=S梯形NOBC – S1
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
M
N
s2
S=S长方形NOMC+S2 – S1
9.如图所示,则四边形AOBC的面积是 。
s1
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
H
s1
s2
S=S1+S2
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
H
s1
s2
s3
S=S1+S2 +S3
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
s1
s2
S=S1+S2
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
M
?
s1
S=S △CMB– S1
9.如图所示,则四边形AOBC的面积是 。
利用现在所学过的知识你能确定M点的坐标吗?
二、利用面积求点的坐标
10. 在平面直角坐标系中,点A,B的坐标分别是(0,1),(0,5),点C在x轴上,如果△ABC的面积为6,求点C的坐标.
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,1)
B(0,5)
11、在平面直角坐标系中,A(1,4),点P在坐标轴上,三角 形PAO的面积等于4,求点P的坐标.
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
A(1,4)
1.直接法求面积
2.割补法求面积
谈谈我们的收获
一题多解
分类讨论
方法
思想
B(0,4)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
A(0,2)
C(-3,2)
?
?
在平面直角坐标系中, △ ABC的顶点坐标分别为A(2,0) B(0,4) C(-3,2)
(1)求△ ABC的面积
(2)若在横轴上有一点P,是的S△AOP=S△AOB,求P点坐标。
(3)若AC交y轴于点Q,求点Q坐标。
-3
已知在平面直角坐标系中,在矩形OABC中,点A(8,0)、 C(0,6)、 D(6,6),点P沿OA边从点O开始沿着O—A---B---D移动,点Q从点C开始,沿着C---B---A移动,用t秒表示移动的时间。
(1)写出点B坐标———
(2)如果P、Q同时出发,点P以1个单位/秒的速度移动,Q的速度是P的速度的2倍,用t秒表示移动的时间,求当△ APM的面积比△ CQM的面积大6时的t值。
1
3
4
2
5
1
2
3
4
5
x
y
o
6
8
7
6
?
?
?
A
B
C
D
Q
P
?
?
?
?
?
M
6
B(3,0)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
? A(0,4)
?
一、根据点的坐标求面积
2.如图所示, △ ABC的面积是 。
C(3,0)
B(-2,0)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
?
? A(0,5)
12.5
B(5,0)
3. 如图所示, △ ABC的面积是 。
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
? C(3, - 4)
H
A(-1,0)
?
?
12
y
4.如图所示, △ ABC的面积是 。
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
H
7.5
? C(0,-2)
A(-3,-1)
?
? B(0,3)
选取在坐标轴上的边作为三角形的底。
5.已知:A(3,5),B(1,2),C(5,2),
则△ ABC的面积 。
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
6
?
?
?
B(1,2)
A(3,5)
C(5,2)
H
6.已知:A(-3,-2),B(-1,3),C(3,3),
则△ ABC的面积是 。
o
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
x
y
A(-3,-2) ?
?
? C(3,3)
B(-1,3)
10
H
7.已知:A(4,2),B(-2,4),C(-2,-1),
则△ ABC的面积是 。
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
? A(4,2)
?
?
C(-2,-1)
15
H
B(-2,4)
选取平行于坐标轴的边作为三角形的底。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
8.如图所示,求△ OAB的面积。
Heng
Ti
Shu
Ti
Heng
Ge
Shu
Ge
P
Quan
bu
Gebu
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
利用现在所学过的知识你能确定M点的坐标吗?
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
N
M
S=S梯形OAMN– S1 –S2
s1
s2
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
S=S梯形OPMB– S1 –S2
P
s1
s2
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
N
M
S=S长方形OPMN– S1 – S2 –S3
P
s1
s2
s3
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
S=S △ BOM+ S梯形BMPA– S △ AOP
P
8.如图所示,求△ OAB的面积。
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
8.如图所示,求△ OAB的面积。
P
返回
Shu
ge
Heng
ge
Ge
bu
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
9.如图所示,则四边形AOBC的面积是 。
13
heng
bu
Bu
chang
xie
ge
Yan
chang
H S
ge
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
N
M
s1
s2
S=S长方形NOBM– S1 –S2
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
N
s1
S=S梯形NOBC – S1
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
M
N
s2
S=S长方形NOMC+S2 – S1
9.如图所示,则四边形AOBC的面积是 。
s1
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
H
s1
s2
S=S1+S2
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
H
s1
s2
s3
S=S1+S2 +S3
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
s1
s2
S=S1+S2
9.如图所示,则四边形AOBC的面积是 。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
M
?
s1
S=S △CMB– S1
9.如图所示,则四边形AOBC的面积是 。
利用现在所学过的知识你能确定M点的坐标吗?
二、利用面积求点的坐标
10. 在平面直角坐标系中,点A,B的坐标分别是(0,1),(0,5),点C在x轴上,如果△ABC的面积为6,求点C的坐标.
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,1)
B(0,5)
11、在平面直角坐标系中,A(1,4),点P在坐标轴上,三角 形PAO的面积等于4,求点P的坐标.
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
A(1,4)
1.直接法求面积
2.割补法求面积
谈谈我们的收获
一题多解
分类讨论
方法
思想
B(0,4)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
A(0,2)
C(-3,2)
?
?
在平面直角坐标系中, △ ABC的顶点坐标分别为A(2,0) B(0,4) C(-3,2)
(1)求△ ABC的面积
(2)若在横轴上有一点P,是的S△AOP=S△AOB,求P点坐标。
(3)若AC交y轴于点Q,求点Q坐标。
-3
已知在平面直角坐标系中,在矩形OABC中,点A(8,0)、 C(0,6)、 D(6,6),点P沿OA边从点O开始沿着O—A---B---D移动,点Q从点C开始,沿着C---B---A移动,用t秒表示移动的时间。
(1)写出点B坐标———
(2)如果P、Q同时出发,点P以1个单位/秒的速度移动,Q的速度是P的速度的2倍,用t秒表示移动的时间,求当△ APM的面积比△ CQM的面积大6时的t值。
1
3
4
2
5
1
2
3
4
5
x
y
o
6
8
7
6
?
?
?
A
B
C
D
Q
P
?
?
?
?
?
M
