人教版七年级数学下册课件:6.1.2平方根(共17张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:6.1.2平方根(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 496.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览






文档简介
教学目标
1.掌握平方根的概念,明确平方根和算术平方根之间的联系和区别。
2.能用符号正确地表示一个数的平方根,理解平方运算和乘方运算之间的互逆关系。
重点难点
重点:平方根的概念和求数的平方根。
难点:平方根和算术平方根的联系与区别。
求下列各式的值。
4
9
2
3
a
2
2
5
5
|a|
±1
x2
1
16
36
49
x
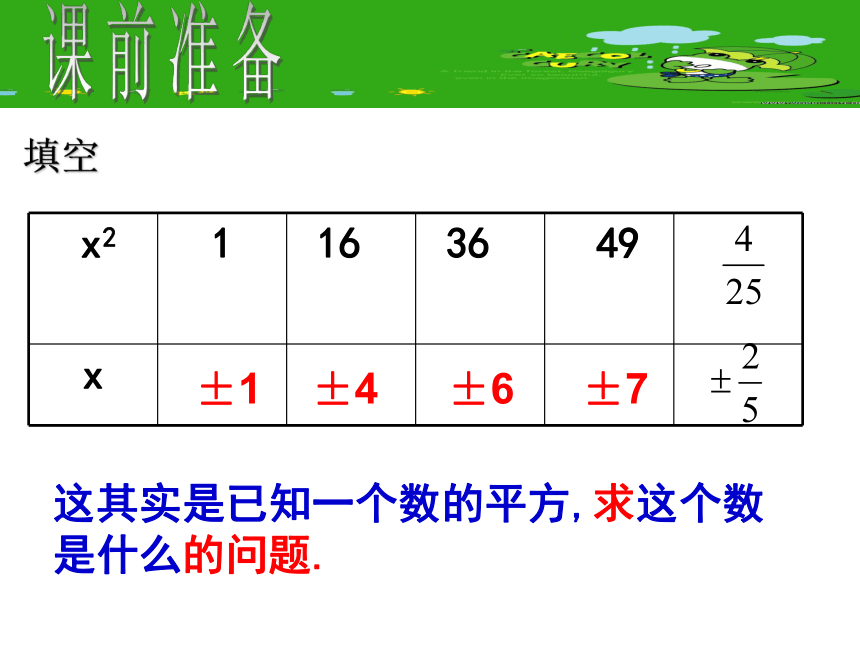
填空
±4
±6
±7
这其实是已知一个数的平方,求这个数是什么的问题.
(±10) =100,
2
那么±10叫做100的平方根;
9的平方根是
∴ ±3;
∵(±3)2 = 9
一般地,如果一个数x的平方等于a,即x2 =a,那么这个数x叫做a的平方根或二次方根
若x2=a,则x是a的平方根或二次方根
求一个数a的平方根的运算,叫做开平方
平方根的概念
平方根
概念:
☆若x2=a,则x是a的
平方根
记作:x=
读作“正负根号a”
平方与开平方运算是互逆运算
☆若x2=a(x≥0)则x是a
的算术平方根
记作:x=
例4
(1)100; (2) (3)0.25;
例4:求下列各数的平方根:
解:(1)∵ (±10)2=100,
∴100的平方根为±10,
即 =±10,
练习
正数有____个平方根,它们____________
0的平方根是_________
负数__________________
总结
2
互为相反数
0
没有平方根
即:非负数才有平方根
正数a的平方根有2个,分别是
正数a的算术平方根
正数a的负的平方根
>0
<0
例5
例5:求下列各数的值:
总结:结果的符号关键看根号前面的符号
课本P47练习第3题
1、求下列各式中x的值
(1)x2=64
(2)4x2=49
(3)
(4)
解方程
(1)(-5)2的平方根是 ,算术平方根 是 ;
±5
5
(2) 的平方根是 ,算术平方 根是 。
±2
2
(3)若x2=3,则 x= ,若 =3,
则 x= ;
±3
2、练习:
(4)若一个数的一个平方根为-7,则另一个平方根为 ,这个数是 。
7
49
(5)若一个正数的两个平方根为2a-6、3a+1,则a= ,这个正数为 ;
1
16
(6)平方根等于本身的数是 ,
算术平方根等于它本身的数是 ,算术平方根和平方根相等的数是 ;
0
0、1
0
3、已知正数m的平方根是2a-3和a-12,求a和m的值。
解:由题意得:
(2a-3)+(a-12)=0
a=5
∴2a-3=7,
∵7是m的一个平方根,
∴m=49
4、已知2a-1的平方根是±3,3a+b-1的算术平方根是4,求a+2b的平方根。
1.掌握平方根的概念,明确平方根和算术平方根之间的联系和区别。
2.能用符号正确地表示一个数的平方根,理解平方运算和乘方运算之间的互逆关系。
重点难点
重点:平方根的概念和求数的平方根。
难点:平方根和算术平方根的联系与区别。
求下列各式的值。
4
9
2
3
a
2
2
5
5
|a|
±1
x2
1
16
36
49
x
填空
±4
±6
±7
这其实是已知一个数的平方,求这个数是什么的问题.
(±10) =100,
2
那么±10叫做100的平方根;
9的平方根是
∴ ±3;
∵(±3)2 = 9
一般地,如果一个数x的平方等于a,即x2 =a,那么这个数x叫做a的平方根或二次方根
若x2=a,则x是a的平方根或二次方根
求一个数a的平方根的运算,叫做开平方
平方根的概念
平方根
概念:
☆若x2=a,则x是a的
平方根
记作:x=
读作“正负根号a”
平方与开平方运算是互逆运算
☆若x2=a(x≥0)则x是a
的算术平方根
记作:x=
例4
(1)100; (2) (3)0.25;
例4:求下列各数的平方根:
解:(1)∵ (±10)2=100,
∴100的平方根为±10,
即 =±10,
练习
正数有____个平方根,它们____________
0的平方根是_________
负数__________________
总结
2
互为相反数
0
没有平方根
即:非负数才有平方根
正数a的平方根有2个,分别是
正数a的算术平方根
正数a的负的平方根
>0
<0
例5
例5:求下列各数的值:
总结:结果的符号关键看根号前面的符号
课本P47练习第3题
1、求下列各式中x的值
(1)x2=64
(2)4x2=49
(3)
(4)
解方程
(1)(-5)2的平方根是 ,算术平方根 是 ;
±5
5
(2) 的平方根是 ,算术平方 根是 。
±2
2
(3)若x2=3,则 x= ,若 =3,
则 x= ;
±3
2、练习:
(4)若一个数的一个平方根为-7,则另一个平方根为 ,这个数是 。
7
49
(5)若一个正数的两个平方根为2a-6、3a+1,则a= ,这个正数为 ;
1
16
(6)平方根等于本身的数是 ,
算术平方根等于它本身的数是 ,算术平方根和平方根相等的数是 ;
0
0、1
0
3、已知正数m的平方根是2a-3和a-12,求a和m的值。
解:由题意得:
(2a-3)+(a-12)=0
a=5
∴2a-3=7,
∵7是m的一个平方根,
∴m=49
4、已知2a-1的平方根是±3,3a+b-1的算术平方根是4,求a+2b的平方根。
