人教版七年级数学下册课件:6.3实数(19张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:6.3实数(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 20:06:41 | ||
图片预览






文档简介
(1)了解无理数和实数的概念
(2)知道实数和数轴上的点一一对应
(3)会求实数的相反数与绝对值。
教学目标
重点难点
重点:正确理解实数的概念。
实数与数轴上的点的一一对应关系。
难点:对“实数与数轴的意义对应关系”的理解。
6.3 实 数
*
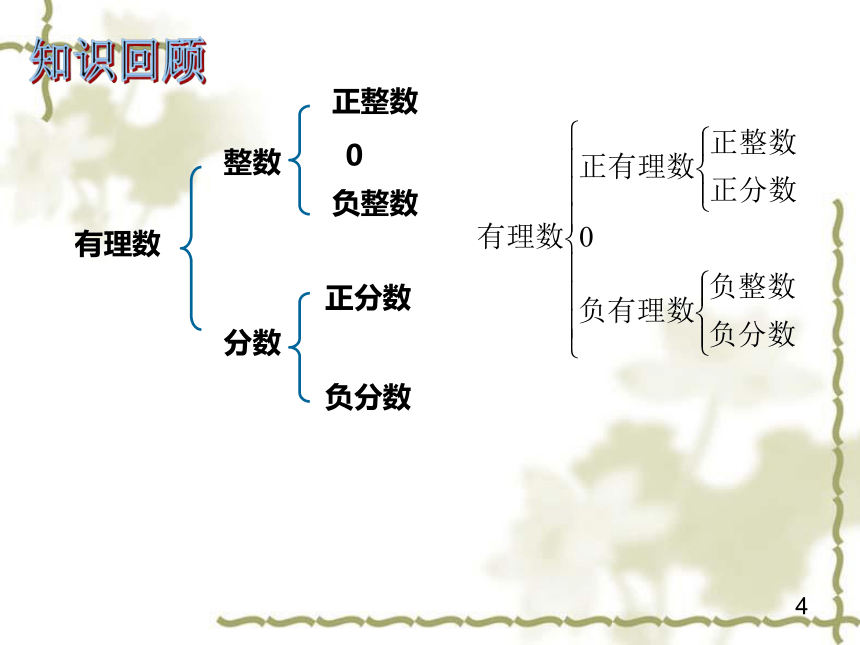
有理数
整数
分数
正整数
负整数
0
正分数
负分数
*
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
*
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
*
无限不循环小数 ---- 叫做无理数.
是有理数吗?
是无理数
你还知道有哪些无理数?
*
实数
实数
有理数
无理数
整数
分数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有理数和无理数统称实数
无限不循环小数
有限小数或无限循环小数
*
判断
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
4.无理数都是无限小数。( )
3.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
×
×
*
6.两个无理数相加有可能是有理数。( )
(2)每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?如果可以你能在数轴上找到表示 这样的无理数的点吗?
(1)有理数能不能将数轴排满?
*
1、直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,,点O,的坐标是多少?
OO?的长是这个圆的周长 ,所以点O?的坐标是
无理数 可以用数轴上的点来表示出来,这也是 的几何意义
*
2、(1)你能用两个面积为1的小正方形拼成一个面积为2的大正方形吗?
它的边长a是多少?
a2 = 2
a 是2的算术平方根,则边长a=
(2)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
-2
-1
0
1
2
B
A
C
所以,每一个无理数都可以用数轴上的一个点表
示出来,也就是说,数轴上的点有些表示有理数,
有些表示无理数.
*
实数与数轴上的点一一对应。即每一个实数都可以用数轴上的一个点来表示;反之数轴上的每一点都表示一个实数。
*
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大。
想一想:当数从有理数扩充到实数后,有理数关于
相反数和绝对值,倒数(不为0)的意义是否同样适
合于实数?
做一做P54“思考”
数a的相反数是____,
-a
这里a表示任意一个实数
一个正实数的绝对值是________ ,
它的本身
一个负实数的绝对值是___________.
它的相反数
如果a 0,那么它的倒数为__________
*
例题1
(1)、分别写出 的相反数
注意:可以化简的数,先化简再看文字要求。
*
例题2
计算下列各式的值
在实数运算中,当遇到无理数并且需要求出结果
的近似值时,可以按照所要求的精确度用相应的
近似值去代替无理数,再进行计算。
比如下面的例题
*
例题3
计算(结果保留小数点后两位)
练习书本p56第2、3、4题
*
已知a,b在数轴上的位置如图.
*
(2)知道实数和数轴上的点一一对应
(3)会求实数的相反数与绝对值。
教学目标
重点难点
重点:正确理解实数的概念。
实数与数轴上的点的一一对应关系。
难点:对“实数与数轴的意义对应关系”的理解。
6.3 实 数
*
有理数
整数
分数
正整数
负整数
0
正分数
负分数
*
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
*
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
*
无限不循环小数 ---- 叫做无理数.
是有理数吗?
是无理数
你还知道有哪些无理数?
*
实数
实数
有理数
无理数
整数
分数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有理数和无理数统称实数
无限不循环小数
有限小数或无限循环小数
*
判断
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
4.无理数都是无限小数。( )
3.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
×
×
*
6.两个无理数相加有可能是有理数。( )
(2)每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?如果可以你能在数轴上找到表示 这样的无理数的点吗?
(1)有理数能不能将数轴排满?
*
1、直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,,点O,的坐标是多少?
OO?的长是这个圆的周长 ,所以点O?的坐标是
无理数 可以用数轴上的点来表示出来,这也是 的几何意义
*
2、(1)你能用两个面积为1的小正方形拼成一个面积为2的大正方形吗?
它的边长a是多少?
a2 = 2
a 是2的算术平方根,则边长a=
(2)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
-2
-1
0
1
2
B
A
C
所以,每一个无理数都可以用数轴上的一个点表
示出来,也就是说,数轴上的点有些表示有理数,
有些表示无理数.
*
实数与数轴上的点一一对应。即每一个实数都可以用数轴上的一个点来表示;反之数轴上的每一点都表示一个实数。
*
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大。
想一想:当数从有理数扩充到实数后,有理数关于
相反数和绝对值,倒数(不为0)的意义是否同样适
合于实数?
做一做P54“思考”
数a的相反数是____,
-a
这里a表示任意一个实数
一个正实数的绝对值是________ ,
它的本身
一个负实数的绝对值是___________.
它的相反数
如果a 0,那么它的倒数为__________
*
例题1
(1)、分别写出 的相反数
注意:可以化简的数,先化简再看文字要求。
*
例题2
计算下列各式的值
在实数运算中,当遇到无理数并且需要求出结果
的近似值时,可以按照所要求的精确度用相应的
近似值去代替无理数,再进行计算。
比如下面的例题
*
例题3
计算(结果保留小数点后两位)
练习书本p56第2、3、4题
*
已知a,b在数轴上的位置如图.
*
