人教版七年级下册数学 9.2 一元一次不等式(共30张ppt)
文档属性
| 名称 | 人教版七年级下册数学 9.2 一元一次不等式(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 645.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览











文档简介
1.经历一元一次不等式概念的形成过程;
2.掌握一元一次不等式的解法,会解简单的一元一次不等式,并能在数轴上将其解集表示出来.
9.2 一元一次不等式
大家已经学习过一元一次方程的定义,你们还记得吗?
知识回顾
只含有一个未知数,未知数的次数是一次,这样的方程叫做一元一次方程.
知识回顾
不等式的性质:
不等式的性质1:
如果a>b,那么a+c>b+c.
不等式的性质2:
如果a>b,并且c>0,那么ac>bc。(或a/c>b/c)
不等式的性质3:
如果a>b,并且c<0,那么ac复习回顾
问题1 观察下面的不等式,它们有哪些共同特征?
一元一次不等式的概念:
含有一个未知数,未知数次数是1的不等式,叫做一元一次不等式.
1. 引入概念
2x-2.5≥15
(2)只含有一个未知数;
完善概念
(1)不等式的两边都是整式;
(3)未知数的次数是1.
?
?
?
?
下列式子哪些是一元一次不等式?
(1) 3x+2>x–1 (2)5x+3<0
(3) +3<5x–1 (4)x(x–1)<2x
(5)3x+5=1; (6)2y-1≤5; (7)
(8)5+2<8 (9)3+2x≥x.
?
?
?
?
?
2x-2.5
你会解下面的方程吗?
探究新知
解一元一次方程的步骤:
1.去分母
2.去括号
3. 移项
4. 合并同类项
5. 系数化为1
探究新知
尝试探索
:解不等式:
(1)x-7<8 (2)3x<2x-3
这两小题中不等式的变形与方程的什么变形相类似?
解:
解:
x-7+7 <8+7
3x-2x <2x-3-2x
移
移
x <8+7
x <15
3x-2x <-3
x <-3
这里的变形与方程中的移项相类似:
注意:移项要变号
例1、 解下列不等式,并将解集在数轴上表示出来: 2x-1<4x+13
解: 2x-1<4x+13,
移项,得 2x-4x<13+1,
合并同类项,得 -2x<14,
系数化为1,得 x>-7.
它在数轴上的表示如下:
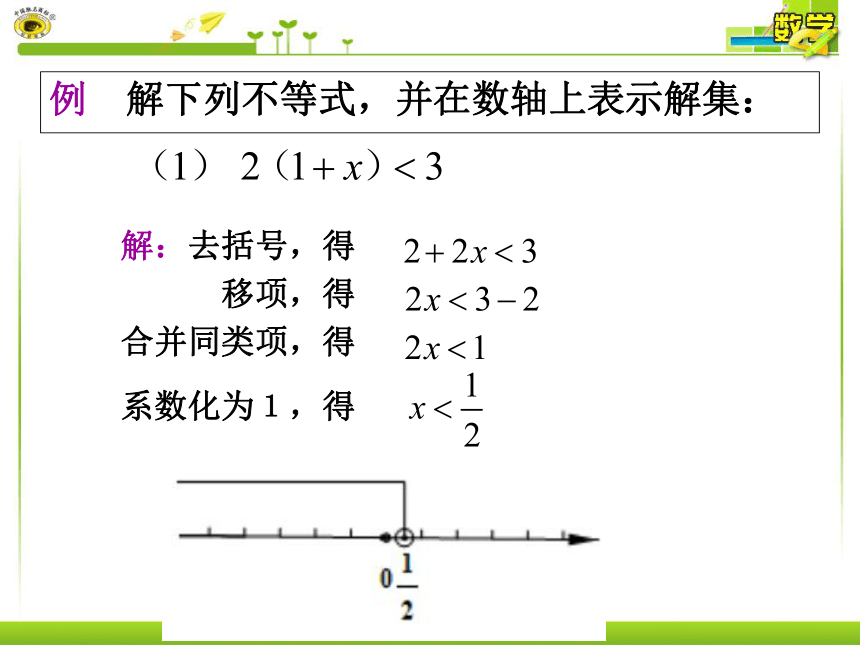
例 解下列不等式,并在数轴上表示解集:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(2)2(5x+3)≤x-3(1-2x)
解 :去括号,得 10x+6≤x-3+6x,
移项 , 得10x-x--6x ≤-3- 6
合并同类项,得 3x≤-9,
系数化为1,得 x≤-3.
它在数轴上的表示如下:
1、解下列不等式,并把解集在数轴上表示出来:
(1)2x+1>3;
(2)2-x<1;
(3)2(x+1)<3x;
(4)3(x+2)≥4(x-1)+7.
做一做
例 解下列不等式,并在数轴上表示解集:
问题(1)
对比不等式 与 的两边,它们在形式上有什么不同?
问题(2)
怎样将不等式 变形,使变形后的不等式不含分母?
例 解下列不等式,并在数轴上表示解集:
解:去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
练习:解不等式 并把解集在数轴上表示出来.
【解析】把原不等式去分母得:6x-9<x+1
移项,合并同类项得:5x<10
把x的系数化为1得:x<2
2
3
1
4
5
6
0
-1
-2
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}步骤
依据
去分母
去括号
移项
合并同类项
系数化为1
不等式的性质2
去括号法则
不等式的性质1
合并同类项法则
不等式的性质2或3
问题3 解一元一次不等式每一步变形的依据是什么?
问题4 解一元一次不等式和解一元一次方程
有哪些相同和不同之处?
相同之处:
基本步骤相同:去分母,去括号,移项,合并同类项,系数化为1.
基本思想相同:都是运用化归思想,将一元一次方程或一元一次不等式变形为最简形式.
不同之处:
(1)解法依据不同:解一元一次不等式的依据是不等式的性质,解一元一次方程的依据是等式的性质.
(2)最简形式不同,一元一次不等式的最简形式是 x>a或x当堂训练
解不等式,并在数轴上表示解集.
(1)5x>-10;
(2)-3x+12≤0;
(3) ;
(4) .
例2、当x取何值时,代数式 与 的值的差大于1?
解:由题意得:
- -- >1
2(x+4)-3(3x-1) >6
2x+8-9x+3 >6
-7x >-5
X <
∴当x< 时,代数式 与 的值的差大于1。
例3 x为何值时式子 的值不小于2
解:由题意,得
解这个不等式,得
例4、求不等式3(1-x) ≤2(x+9)的负整数解.
解:解不等式3(1-x) ≤2(x+9),得x≥-3
因为x为负整数
所以x=-3,-2,-1.
会做了吗,试一试.
求不等式2 (x-1) <x+1的正整数解.
二、求一元一次不等式的特殊解:
通过本课时的学习,需要我们掌握:
1.一元一次不等式的概念;
2.一元一次不等式的解法与一元一次方程的解法类似,
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)化系数为1(有时不等号的方向会改变哦!)
布置作业
1.必做题:
解下列不等式,并把解集在数轴上表示出来.
(1)5x+15>4x-1 ; (2)2(x+5)<3(x-5);
(3) < ; (4) < +1 .
2.选做题:
求下列不等式的正整数解.
(1)-4x>-12;(2)3x-9≤0.
解不等式,并在数轴上表示解集.
(1)
(2)2(2x-3)<5(x- 1).
当堂检测:
3.解不等式 ,并把它的解集在数轴上
表示出来.
例3 小颖准备用21元钱买笔和笔记本.已知每支笔3元,每个笔记本2.2元,她买了2个笔记本.请你帮她算一算,她还可能买几支笔?
【解析】设她还可能买n支笔,根据题意得
3n+2.2×2≤21
解得,n≤
因为在这个问题中n只能取正整数,所以小颖还可能买1支、2支、3支、4支或5支笔.
2.亮亮准备用节省的零花钱买一台复读机,他已存有45
元,计划从现在起以后每月节省30元,直到他至少有300
元.设x个月后他至少有300元,则符合题意的不等式是
( )
(A)30x-45≥300 (B)30x+45≥300
(C)30x-45≤300 (D)30x+45≤300
【解析】选B.由于亮亮每个月节省30元,故x个月后他可以节省30x元,此时亮亮有(30x+45)元.根据题意得30x+ 45≥300,故选B.
一个有信念者所开发出的力量,大于99个只有兴趣者。
2.掌握一元一次不等式的解法,会解简单的一元一次不等式,并能在数轴上将其解集表示出来.
9.2 一元一次不等式
大家已经学习过一元一次方程的定义,你们还记得吗?
知识回顾
只含有一个未知数,未知数的次数是一次,这样的方程叫做一元一次方程.
知识回顾
不等式的性质:
不等式的性质1:
如果a>b,那么a+c>b+c.
不等式的性质2:
如果a>b,并且c>0,那么ac>bc。(或a/c>b/c)
不等式的性质3:
如果a>b,并且c<0,那么ac
问题1 观察下面的不等式,它们有哪些共同特征?
一元一次不等式的概念:
含有一个未知数,未知数次数是1的不等式,叫做一元一次不等式.
1. 引入概念
2x-2.5≥15
(2)只含有一个未知数;
完善概念
(1)不等式的两边都是整式;
(3)未知数的次数是1.
?
?
?
?
下列式子哪些是一元一次不等式?
(1) 3x+2>x–1 (2)5x+3<0
(3) +3<5x–1 (4)x(x–1)<2x
(5)3x+5=1; (6)2y-1≤5; (7)
(8)5+2<8 (9)3+2x≥x.
?
?
?
?
?
2x-2.5
你会解下面的方程吗?
探究新知
解一元一次方程的步骤:
1.去分母
2.去括号
3. 移项
4. 合并同类项
5. 系数化为1
探究新知
尝试探索
:解不等式:
(1)x-7<8 (2)3x<2x-3
这两小题中不等式的变形与方程的什么变形相类似?
解:
解:
x-7+7 <8+7
3x-2x <2x-3-2x
移
移
x <8+7
x <15
3x-2x <-3
x <-3
这里的变形与方程中的移项相类似:
注意:移项要变号
例1、 解下列不等式,并将解集在数轴上表示出来: 2x-1<4x+13
解: 2x-1<4x+13,
移项,得 2x-4x<13+1,
合并同类项,得 -2x<14,
系数化为1,得 x>-7.
它在数轴上的表示如下:
例 解下列不等式,并在数轴上表示解集:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(2)2(5x+3)≤x-3(1-2x)
解 :去括号,得 10x+6≤x-3+6x,
移项 , 得10x-x--6x ≤-3- 6
合并同类项,得 3x≤-9,
系数化为1,得 x≤-3.
它在数轴上的表示如下:
1、解下列不等式,并把解集在数轴上表示出来:
(1)2x+1>3;
(2)2-x<1;
(3)2(x+1)<3x;
(4)3(x+2)≥4(x-1)+7.
做一做
例 解下列不等式,并在数轴上表示解集:
问题(1)
对比不等式 与 的两边,它们在形式上有什么不同?
问题(2)
怎样将不等式 变形,使变形后的不等式不含分母?
例 解下列不等式,并在数轴上表示解集:
解:去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
练习:解不等式 并把解集在数轴上表示出来.
【解析】把原不等式去分母得:6x-9<x+1
移项,合并同类项得:5x<10
把x的系数化为1得:x<2
2
3
1
4
5
6
0
-1
-2
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}步骤
依据
去分母
去括号
移项
合并同类项
系数化为1
不等式的性质2
去括号法则
不等式的性质1
合并同类项法则
不等式的性质2或3
问题3 解一元一次不等式每一步变形的依据是什么?
问题4 解一元一次不等式和解一元一次方程
有哪些相同和不同之处?
相同之处:
基本步骤相同:去分母,去括号,移项,合并同类项,系数化为1.
基本思想相同:都是运用化归思想,将一元一次方程或一元一次不等式变形为最简形式.
不同之处:
(1)解法依据不同:解一元一次不等式的依据是不等式的性质,解一元一次方程的依据是等式的性质.
(2)最简形式不同,一元一次不等式的最简形式是 x>a或x当堂训练
解不等式,并在数轴上表示解集.
(1)5x>-10;
(2)-3x+12≤0;
(3) ;
(4) .
例2、当x取何值时,代数式 与 的值的差大于1?
解:由题意得:
- -- >1
2(x+4)-3(3x-1) >6
2x+8-9x+3 >6
-7x >-5
X <
∴当x< 时,代数式 与 的值的差大于1。
例3 x为何值时式子 的值不小于2
解:由题意,得
解这个不等式,得
例4、求不等式3(1-x) ≤2(x+9)的负整数解.
解:解不等式3(1-x) ≤2(x+9),得x≥-3
因为x为负整数
所以x=-3,-2,-1.
会做了吗,试一试.
求不等式2 (x-1) <x+1的正整数解.
二、求一元一次不等式的特殊解:
通过本课时的学习,需要我们掌握:
1.一元一次不等式的概念;
2.一元一次不等式的解法与一元一次方程的解法类似,
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)化系数为1(有时不等号的方向会改变哦!)
布置作业
1.必做题:
解下列不等式,并把解集在数轴上表示出来.
(1)5x+15>4x-1 ; (2)2(x+5)<3(x-5);
(3) < ; (4) < +1 .
2.选做题:
求下列不等式的正整数解.
(1)-4x>-12;(2)3x-9≤0.
解不等式,并在数轴上表示解集.
(1)
(2)2(2x-3)<5(x- 1).
当堂检测:
3.解不等式 ,并把它的解集在数轴上
表示出来.
例3 小颖准备用21元钱买笔和笔记本.已知每支笔3元,每个笔记本2.2元,她买了2个笔记本.请你帮她算一算,她还可能买几支笔?
【解析】设她还可能买n支笔,根据题意得
3n+2.2×2≤21
解得,n≤
因为在这个问题中n只能取正整数,所以小颖还可能买1支、2支、3支、4支或5支笔.
2.亮亮准备用节省的零花钱买一台复读机,他已存有45
元,计划从现在起以后每月节省30元,直到他至少有300
元.设x个月后他至少有300元,则符合题意的不等式是
( )
(A)30x-45≥300 (B)30x+45≥300
(C)30x-45≤300 (D)30x+45≤300
【解析】选B.由于亮亮每个月节省30元,故x个月后他可以节省30x元,此时亮亮有(30x+45)元.根据题意得30x+ 45≥300,故选B.
一个有信念者所开发出的力量,大于99个只有兴趣者。
