人教版七年级下册数学 6.1 平方根 课件(共36张PPT)
文档属性
| 名称 | 人教版七年级下册数学 6.1 平方根 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览










文档简介
(共36张PPT)
6.1平方根
同学们,你们知道宇宙飞船离开地球进入轨道正常运行的速度是什么范围吗?这时它的速度要大于第一个宇宙的速度v1(米/秒)而小于第二宇宙速度v2(米/秒)。v1、v2的大小满足v12=gR, v22=2gR,其中g是物理中的一个常数(重力加速度),g≈9.8米/秒2,R是地球的半径,R≈6.4×106米。怎样求v1、v2呢?这就要用到平方根的概念。
随着人类对数的认识的不断发展,人们从现实世界抽象出一种不同于有理数的数——无理数。有理数和无理数合起来形成了一种新的数——实数。本章将从平方根与立方根等说起,学习有关实数的初步知识,并用这些知识解决一些实际问题。
我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。
在这五种运算中那些是逆运算呢
★加法与减法互为逆运算;
★乘法与除法互为逆运算;
★那么乘方与谁互为逆运算呢?
回忆与思考:
我们先来复习乘方的有关内容:
底数
幂
指数
m个a
回忆与思考:
5厘米
要剪出一张边长是5厘米的正方形纸片,它的面积是多少?
这个问题实际上就是求:
答:它的面积是25平方厘 米
这是已知底数和指数,求幂的运算
乘方运算
?厘米
我们把问题反过来,要做一张面积是25平方厘米的方桌面,它的边长是多少厘米?
实际上就是要求出一个数,使它的平方等于25,即:
显然,括号里应是±5,但
-5不符题意。
∴方桌面的边长应是5厘米。
25平方厘米
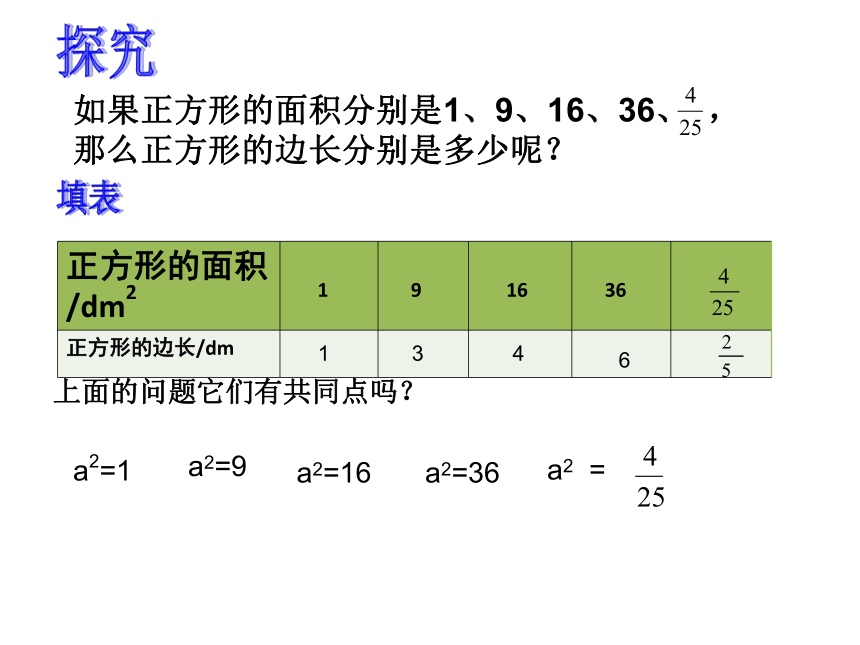
如果正方形的面积分别是1、9、16、36、 ,那么正方形的边长分别是多少呢?
探究
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
1
3
4
6
填表
上面的问题它们有共同点吗?
a2=1
a2=9
a2=16
a2=36
a2 =
归纳:
⑴算术平方根的概念:
一般地,如果一个正数x的平方等于a,即x2=a那么这个正数x叫做a的算术平方根。
⑵算术平方根的表示方法:
a的算术平方根记为 ,读作“根号a”或“二次根号a”,a叫做被开方数。
显然,平方和开平方互为逆运算。
(3) 求一个数的算数平方根的运算叫做开平方。
例1、求下列各数的算术平方根:
应用
(1)100 (2) (3) (4) (5)0
解:⑴因为 所以100的算术平方根是10,即 ;
(2)因为 ,所以 的算术平方根是 ,即 ;
(4)因为 0.012=0.0001,所以0.0001的算术平方根是0.01,即
⑶因为 ,所以 的算术平方根是 ,即 ;
(5)因为02=0,所以0的算术平方根是0,即 ;
练习
1.求下列各数的算术平方根;
(1)0.002 5 (2)81 (3)32
判断:
(1)5是25的算术平方根;
(2)-6是 36 的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-5是-25的算术平方根。
(1) 16的算术平方根是______
(3) 的算术平方根是______
4
(2) 的值是______
4
2
0和1
0
正
练一练
1.判断题
① 的算术平方根是± ( )
③一个正数的算术平方根总小于它本身( )
②5是 的算术平方根 ( )
3.回答下列各数的算术平方根
0.000 001
2.填空题
① 正数的算术平方根是 数,0的算术平方根是 ,算术平方根等于它本身的数是
② 的算术平方根是
③ 的算术平方根的相反数的绝对值是
解 = =
4.求 的值
√
×
×
4
①根据算术平方根的定义解题,明确平方与开平方互为逆运算;
②求带分数的算术平方根,需要先把带分数化成假分数,然后根据定义去求解;
③0的算术平方根是0。
注意
算术平方根的性质
正数有一个正的算术平方根,
0 有一个算术平方根—— 0 ,
负数没有算术平方根。
结论:
例2 求下列各式的值:
(1) (2) (3) (4)
解:(1) (2)
(3) (4)
例3 求下列各数的算术平方根:
⑴ ⑵ ⑶ ⑷
练习
2.求下列各数的值;
探究
1、a可以取任何数吗?
2、 是什么数?
被开方数a是非负数
也就是说,非负数的“算术”平方根是非负数。负数不存在算术平方根,即当 时, 无意义。
如: 无意义 ; 8是64的算术平方根或 。
3 、 是算术平方根的运算符号
算术平方根具有双重非负性
思考:
1.下列各式哪些有意义,哪些没
有意义?
(1)- (2)
(3) (4)
学以致用
四、我理解、我会用:
到目前为止,表示非负数的式子有:
a≥0, |a|≥0
1.若|a+3|=0 则a= ,若
则m= ,若
若|a-3|+
的值为 。
≥0
则 a=
,则代数式
-3
7
5
-1
五、强化训练
1、计算
=
=
=
=
=
=
2
由此可知:对于任意数 ,都有 =_____.
5
3
6
7
0
五、强化训练
2、计算
=
=
=
=
=
=
由此可知: 对于任意非负数 , 都有 =_____.
4
25
49
0
36
9
小结:这节课我们学到了哪些知识
(1)如果一个正数的平方等于a,这个正数叫做a的算术平方根;
(2)0的算术平方根仍是0
(3)求一个正数的算术平方根.
四、我理解、我会用:
到目前为止,表示非负数的式子有:
a≥0, |a|≥0
1.若|a+3|=0 则a= ,若
则m= ,若
若|a-3|+
的值为 。
≥0
则 a=
,则代数式
-3
7
5
-1
五、强化训练
1、计算
=
=
=
=
=
=
2
由此可知:对于任意数 ,都有 =_____.
5
3
6
7
0
五、强化训练
2、计算
=
=
=
=
=
=
由此可知: 对于任意非负数 , 都有 =_____.
4
25
49
0
36
9
随堂训练
小结:这节课我们学到了哪些知识
(1)如果一个正数的平方等于a,这个正数叫做a的算术平方根;
(2)0的算术平方根仍是0
(3)求一个正数的算术平方根.
1、下列各数没有算术平方根的是( )
A. 0 B.16 C.-4 D.2
2、若数a的算术平方根等于3,则a的 值是( )
A. 3 B. -3 C. -9 D.9
C
D
认真选一选
D
一、 a的算术平方根(a>0)怎么表示___________.
二、 =9, 则3是9的__________,
表示为______.
三、0的算术平方根是_______,表示
为________.
算术平方根
0
0
=
0
a
2
3
练一练
四、下列各式中哪些有意义?哪些无意义?为什么?
答:有意义的是
无意义的是
(
)
2
;
3
;
3
;
3
;
5
-
-
-
6.1平方根
同学们,你们知道宇宙飞船离开地球进入轨道正常运行的速度是什么范围吗?这时它的速度要大于第一个宇宙的速度v1(米/秒)而小于第二宇宙速度v2(米/秒)。v1、v2的大小满足v12=gR, v22=2gR,其中g是物理中的一个常数(重力加速度),g≈9.8米/秒2,R是地球的半径,R≈6.4×106米。怎样求v1、v2呢?这就要用到平方根的概念。
随着人类对数的认识的不断发展,人们从现实世界抽象出一种不同于有理数的数——无理数。有理数和无理数合起来形成了一种新的数——实数。本章将从平方根与立方根等说起,学习有关实数的初步知识,并用这些知识解决一些实际问题。
我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。
在这五种运算中那些是逆运算呢
★加法与减法互为逆运算;
★乘法与除法互为逆运算;
★那么乘方与谁互为逆运算呢?
回忆与思考:
我们先来复习乘方的有关内容:
底数
幂
指数
m个a
回忆与思考:
5厘米
要剪出一张边长是5厘米的正方形纸片,它的面积是多少?
这个问题实际上就是求:
答:它的面积是25平方厘 米
这是已知底数和指数,求幂的运算
乘方运算
?厘米
我们把问题反过来,要做一张面积是25平方厘米的方桌面,它的边长是多少厘米?
实际上就是要求出一个数,使它的平方等于25,即:
显然,括号里应是±5,但
-5不符题意。
∴方桌面的边长应是5厘米。
25平方厘米
如果正方形的面积分别是1、9、16、36、 ,那么正方形的边长分别是多少呢?
探究
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
1
3
4
6
填表
上面的问题它们有共同点吗?
a2=1
a2=9
a2=16
a2=36
a2 =
归纳:
⑴算术平方根的概念:
一般地,如果一个正数x的平方等于a,即x2=a那么这个正数x叫做a的算术平方根。
⑵算术平方根的表示方法:
a的算术平方根记为 ,读作“根号a”或“二次根号a”,a叫做被开方数。
显然,平方和开平方互为逆运算。
(3) 求一个数的算数平方根的运算叫做开平方。
例1、求下列各数的算术平方根:
应用
(1)100 (2) (3) (4) (5)0
解:⑴因为 所以100的算术平方根是10,即 ;
(2)因为 ,所以 的算术平方根是 ,即 ;
(4)因为 0.012=0.0001,所以0.0001的算术平方根是0.01,即
⑶因为 ,所以 的算术平方根是 ,即 ;
(5)因为02=0,所以0的算术平方根是0,即 ;
练习
1.求下列各数的算术平方根;
(1)0.002 5 (2)81 (3)32
判断:
(1)5是25的算术平方根;
(2)-6是 36 的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-5是-25的算术平方根。
(1) 16的算术平方根是______
(3) 的算术平方根是______
4
(2) 的值是______
4
2
0和1
0
正
练一练
1.判断题
① 的算术平方根是± ( )
③一个正数的算术平方根总小于它本身( )
②5是 的算术平方根 ( )
3.回答下列各数的算术平方根
0.000 001
2.填空题
① 正数的算术平方根是 数,0的算术平方根是 ,算术平方根等于它本身的数是
② 的算术平方根是
③ 的算术平方根的相反数的绝对值是
解 = =
4.求 的值
√
×
×
4
①根据算术平方根的定义解题,明确平方与开平方互为逆运算;
②求带分数的算术平方根,需要先把带分数化成假分数,然后根据定义去求解;
③0的算术平方根是0。
注意
算术平方根的性质
正数有一个正的算术平方根,
0 有一个算术平方根—— 0 ,
负数没有算术平方根。
结论:
例2 求下列各式的值:
(1) (2) (3) (4)
解:(1) (2)
(3) (4)
例3 求下列各数的算术平方根:
⑴ ⑵ ⑶ ⑷
练习
2.求下列各数的值;
探究
1、a可以取任何数吗?
2、 是什么数?
被开方数a是非负数
也就是说,非负数的“算术”平方根是非负数。负数不存在算术平方根,即当 时, 无意义。
如: 无意义 ; 8是64的算术平方根或 。
3 、 是算术平方根的运算符号
算术平方根具有双重非负性
思考:
1.下列各式哪些有意义,哪些没
有意义?
(1)- (2)
(3) (4)
学以致用
四、我理解、我会用:
到目前为止,表示非负数的式子有:
a≥0, |a|≥0
1.若|a+3|=0 则a= ,若
则m= ,若
若|a-3|+
的值为 。
≥0
则 a=
,则代数式
-3
7
5
-1
五、强化训练
1、计算
=
=
=
=
=
=
2
由此可知:对于任意数 ,都有 =_____.
5
3
6
7
0
五、强化训练
2、计算
=
=
=
=
=
=
由此可知: 对于任意非负数 , 都有 =_____.
4
25
49
0
36
9
小结:这节课我们学到了哪些知识
(1)如果一个正数的平方等于a,这个正数叫做a的算术平方根;
(2)0的算术平方根仍是0
(3)求一个正数的算术平方根.
四、我理解、我会用:
到目前为止,表示非负数的式子有:
a≥0, |a|≥0
1.若|a+3|=0 则a= ,若
则m= ,若
若|a-3|+
的值为 。
≥0
则 a=
,则代数式
-3
7
5
-1
五、强化训练
1、计算
=
=
=
=
=
=
2
由此可知:对于任意数 ,都有 =_____.
5
3
6
7
0
五、强化训练
2、计算
=
=
=
=
=
=
由此可知: 对于任意非负数 , 都有 =_____.
4
25
49
0
36
9
随堂训练
小结:这节课我们学到了哪些知识
(1)如果一个正数的平方等于a,这个正数叫做a的算术平方根;
(2)0的算术平方根仍是0
(3)求一个正数的算术平方根.
1、下列各数没有算术平方根的是( )
A. 0 B.16 C.-4 D.2
2、若数a的算术平方根等于3,则a的 值是( )
A. 3 B. -3 C. -9 D.9
C
D
认真选一选
D
一、 a的算术平方根(a>0)怎么表示___________.
二、 =9, 则3是9的__________,
表示为______.
三、0的算术平方根是_______,表示
为________.
算术平方根
0
0
=
0
a
2
3
练一练
四、下列各式中哪些有意义?哪些无意义?为什么?
答:有意义的是
无意义的是
(
)
2
;
3
;
3
;
3
;
5
-
-
-
