人教版数学八年级下册20.1《平均数(1)》 课件(共30张PPT)
文档属性
| 名称 | 人教版数学八年级下册20.1《平均数(1)》 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 18:57:40 | ||
图片预览









文档简介
20.1平均数(1)
人教版八年级(下册)
数学是人们在生活、生产实践中产生出来的一门科学,同时学好数学又是为社会、生活所服务。现代信息社会中,大量的数据信息统计就是数学知识应用的一个重要方面。
平均数---是数据分析中被常用的一组数据代表。
教学目标
从贴近生活的问题情景出发,让学生经历操作、观察、对比、分析、交流等探究活动,通过解决问题的过程,深化对权的各种形式的理解和认识,并掌握加权平均数的计算方法,并能利用其解决不同情境下的实际问题。培养学生科学严谨的分析数据的精神和数学思维。
教学重点
权及加权平均数的概念的理解,计算公式及应用。
教学难点
加权平均数概念的形成。
创设情境引入新课
我校初二年级为迎接5月份中考微机考试,上周进行微机模拟,为反映我班微机成绩,现随机抽取我班10名同学的考试成绩,分值如下:
7 7 8 8 9 10 9 8 9 8
请同学们计算这10名同学的平均成绩。
日常生活中,我们常用平均数表示一组
数据的“平均水平”。
一般地,对于 个数 ,我们把
叫做这n个数的算术平均数,简称平均数,记为 。
20.1.1 平均数
=
算术平均数的概念:
创设情境引入新课
我校初二年级为迎接5月份中考微机考试,上周进行微机模拟,为反映我班微机成绩,现随机抽取我班10名同学的考试成绩,分值如下:
7 7 8 8 9 10 9 8 9 8
请同学们计算这10名同学的平均成绩。
自主探究形成概念
一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示:
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
(1)如果这家公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩(百分制),从他们的成绩看,应该录取谁??
自主探究形成概念
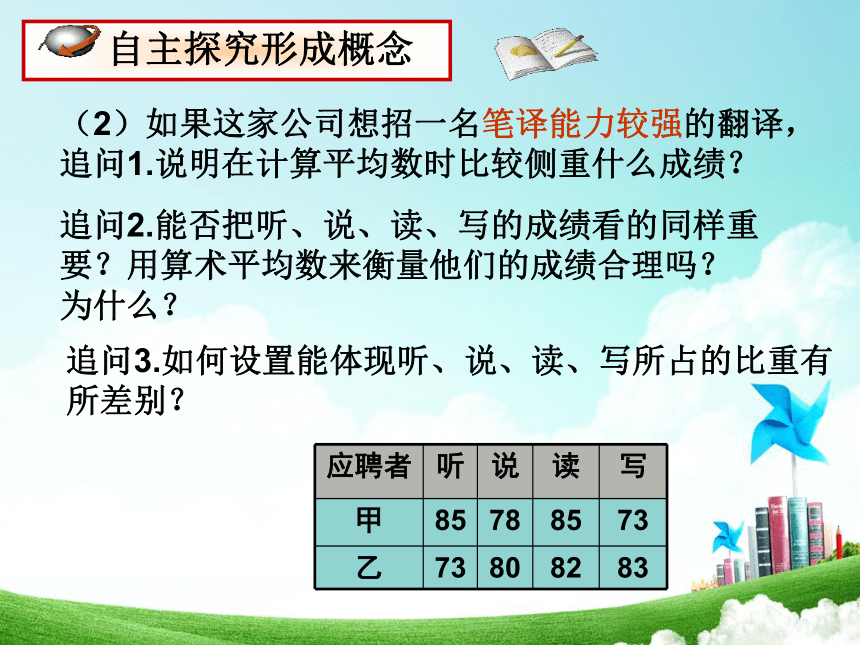
(2)如果这家公司想招一名笔译能力较强的翻译,追问1.说明在计算平均数时比较侧重什么成绩?
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
追问2.能否把听、说、读、写的成绩看的同样重要?用算术平均数来衡量他们的成绩合理吗?为什么?
追问3.如何设置能体现听、说、读、写所占的比重有所差别?
自主探究形成概念
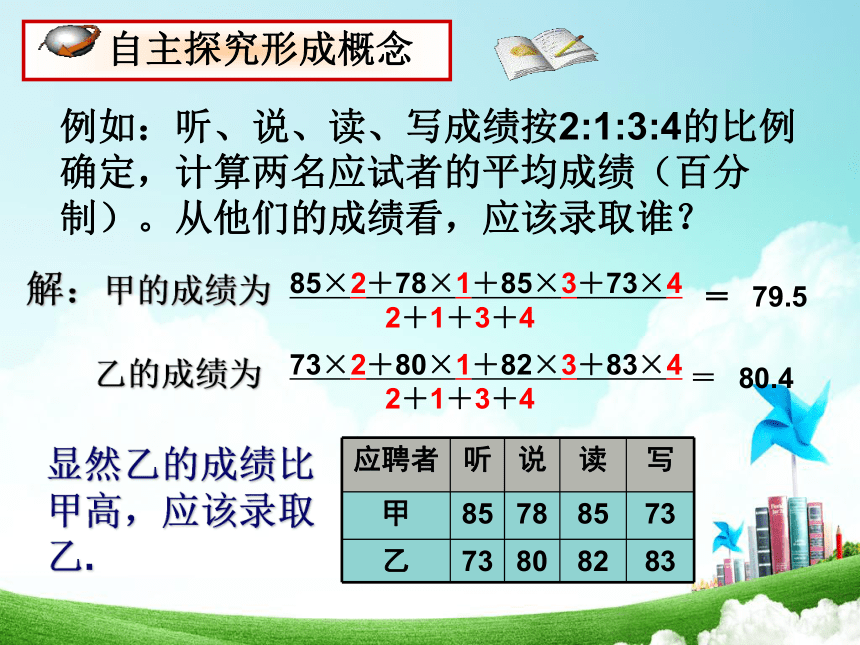
例如:听、说、读、写成绩按2:1:3:4的比例确定,计算两名应试者的平均成绩(百分制)。从他们的成绩看,应该录取谁?
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:甲的成绩为
85×2+78×1+85×3+73×4
2+1+3+4
=
80.4
乙的成绩为
73×2+80×1+82×3+83×4
2+1+3+4
=
79.5
显然乙的成绩比甲高,应该录取乙.
自主探究形成概念
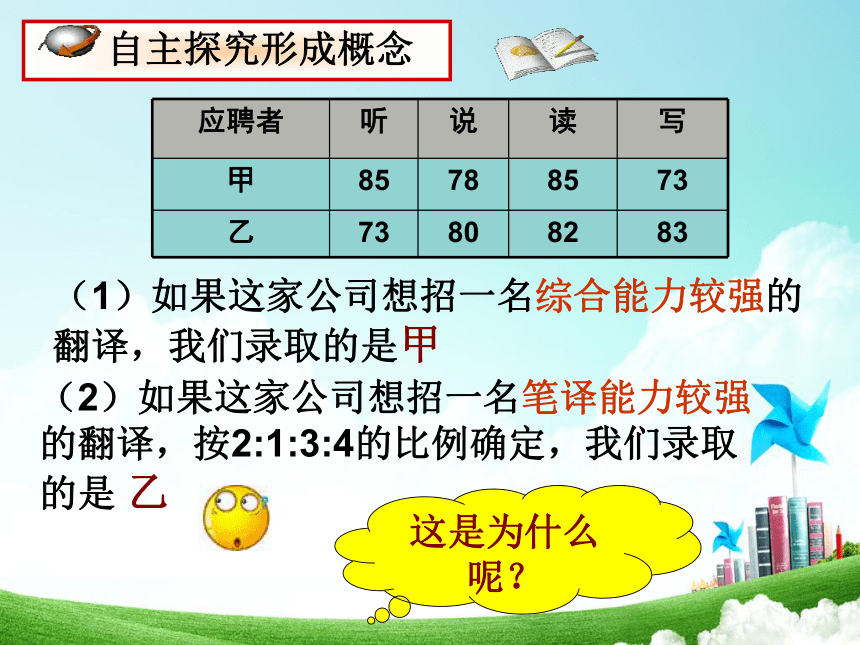
(1)如果这家公司想招一名综合能力较强的翻译,我们录取的是甲
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
(2)如果这家公司想招一名笔译能力较强的翻译,按2:1:3:4的比例确定,我们录取的是 乙
这是为什么呢?
能否把这种加权平均数的计算方法推广到一般吗?
加权平均数的概念:
,...,
叫做这 个数的加权平均数。
n
2
w
,
1
w
w
n
,...,
,
2
1
的权分别是
个数
若
x
x
x
n
n
则
...
...
2
1
2
2
1
1
w
w
w
w
x
w
x
w
x
n
n
n
+
+
+
+
+
+
=
85×2+78×1+85×3+75×4
2+1+3+4
73×2+80×1+82×3+83×4
2+1+3+4
辨析
算术平均数与加权平均数的区别与联系:
(2) 在实际问题中,各项权不相等时,计算平均数时
就要采用加权平均数,当各项权相等时,计算平均数
就要采用算术平均数。
(1) 算术平均数是加权平均数的一种特殊情况
(它特殊在各项的权相等)
理解新知,巩固加深
(3)如果这家公司想招一名口语能力较强的翻译,应该侧重什么成绩?
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:甲的成绩为
85×3+78×3+85×2+73×2
3+3+2+2
=
78.9
乙的成绩为
73×3+80×3+82×2+83×2
3+3+2+2
=
80.5
显然甲的成绩比甲高,应该录取甲.
若听、说、读、写的成绩按照3:3:2:2的比确定,则应该录取谁?
如何设置能够体现听、说、读、写所占的比重有所差别呢?
自主探究形成概念
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
(2)如果这家公司想招一名笔译能力较强的翻译,按2:1:3:4的比例确定,我们录取的是 乙
大家能体会到权的作用吗
(3)如果这家公司想招一名口语能力较强的翻译,按3:3:2:2的比例确定,我们录取的是 甲
例2 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
思考(1)你认为在计算选手的综合成绩时侧重于哪个方面的成绩?三项成绩的权分别是多少?此时的权是以什么形式表现的?
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考(2)利用加权平均数公式你能求出A、B的综合成绩,决出两人的名次吗?
认真思考,一定能回答正确的。
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考:同学们观察表格中两名选手的单项成绩,你发现什么了?为什么他们的最后得分不同?从中你能体会到权的作用吗?
选手A的95分是演讲能力,B的95分是演讲内容,而根据题意可知,演讲内容所占的权重比演讲能力所占的权重大,所以A的95分就不如B的95分在综合成绩中占的分值大.在此更能显示出“权”的重要性.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
你真正理解了吗?
原题再现
我校初二年级为迎接5月份中考微机考试,上周进行微机模拟考试,现随机抽取我班10名同学的考试成绩,分值如下:
7 7 8 8 9 10 9 8 9 8
请同学们计算这10名同学的平均成绩。
7×2+8×4+9×3+10×1
2+4+3+1
=
8.3
总结反思
谈一谈本节课你有哪些收获?
你学会了哪些知识?
理解了哪个字的含义?
还从这节课的学习中悟到了哪些数学思想?
能否把这种加权平均数的计算方法推广到一般吗?
加权平均数的概念:
,...,
叫做这 个数的加权平均数。
n
2
w
,
1
w
w
n
,...,
,
2
1
的权分别是
个数
若
x
x
x
n
n
则
...
...
2
1
2
2
1
1
w
w
w
w
x
w
x
w
x
n
n
n
+
+
+
+
+
+
=
85×2+78×1+85×3+75×4
2+1+3+4
73×2+80×1+82×3+83×4
2+1+3+4
表格所示我校初二年级本次期中考试各班数学成绩的平均分,请同学们求我校这次数学考试的平均成绩
班级
1
2
3
4
参考人
40
42
45
30
平均分
81
80
82
79
仔细完成哦
当堂检验
课后练习1. 2
自主探究形成概念
例如:听、说、读、写成绩按2:1:3:4的比例确定,计算两名应试者的平均成绩(百分制)。从他们的成绩看,应该录取谁?
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:甲的成绩为
85×2+83×1+78×3+75×4
2+1+3+4
=
80.4
乙的成绩为
73×2+80×1+82×3+73×4
2+1+3+4
=
79.5
显然乙的成绩比甲高,应该录取乙.
人教版初中数学八年级下 平均数
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
思考(1)这家公司在招聘英文翻译时,对甲乙两名应试者进行了哪几方面的英语水平测试?成绩分别是多少?
思考(2)招口语能力较强的翻译,“听、说、读、写成绩按照3∶3∶2∶2的比确定”,说明公司侧重于哪几个方面的成绩?
思考(3)计算两名候选人的平均成绩实际上就是求两人听、说、读、写四项成绩的加权平均数,那么它们的权分别是什么?
认真思考,你一定行的.
加权平均数的意义
在一组数据中,由于每个数据的权不同,所以计算平均数时,用加权平均数,才符合实际.
数据的权的意义
数据的权能够反映数据的相对“重要程度”.
权的三种表现形式
1、直接以数据形式给出;
2、比例形式给出;
3、百分数形式给出.
人教版八年级(下册)
数学是人们在生活、生产实践中产生出来的一门科学,同时学好数学又是为社会、生活所服务。现代信息社会中,大量的数据信息统计就是数学知识应用的一个重要方面。
平均数---是数据分析中被常用的一组数据代表。
教学目标
从贴近生活的问题情景出发,让学生经历操作、观察、对比、分析、交流等探究活动,通过解决问题的过程,深化对权的各种形式的理解和认识,并掌握加权平均数的计算方法,并能利用其解决不同情境下的实际问题。培养学生科学严谨的分析数据的精神和数学思维。
教学重点
权及加权平均数的概念的理解,计算公式及应用。
教学难点
加权平均数概念的形成。
创设情境引入新课
我校初二年级为迎接5月份中考微机考试,上周进行微机模拟,为反映我班微机成绩,现随机抽取我班10名同学的考试成绩,分值如下:
7 7 8 8 9 10 9 8 9 8
请同学们计算这10名同学的平均成绩。
日常生活中,我们常用平均数表示一组
数据的“平均水平”。
一般地,对于 个数 ,我们把
叫做这n个数的算术平均数,简称平均数,记为 。
20.1.1 平均数
=
算术平均数的概念:
创设情境引入新课
我校初二年级为迎接5月份中考微机考试,上周进行微机模拟,为反映我班微机成绩,现随机抽取我班10名同学的考试成绩,分值如下:
7 7 8 8 9 10 9 8 9 8
请同学们计算这10名同学的平均成绩。
自主探究形成概念
一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示:
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
(1)如果这家公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩(百分制),从他们的成绩看,应该录取谁??
自主探究形成概念
(2)如果这家公司想招一名笔译能力较强的翻译,追问1.说明在计算平均数时比较侧重什么成绩?
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
追问2.能否把听、说、读、写的成绩看的同样重要?用算术平均数来衡量他们的成绩合理吗?为什么?
追问3.如何设置能体现听、说、读、写所占的比重有所差别?
自主探究形成概念
例如:听、说、读、写成绩按2:1:3:4的比例确定,计算两名应试者的平均成绩(百分制)。从他们的成绩看,应该录取谁?
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:甲的成绩为
85×2+78×1+85×3+73×4
2+1+3+4
=
80.4
乙的成绩为
73×2+80×1+82×3+83×4
2+1+3+4
=
79.5
显然乙的成绩比甲高,应该录取乙.
自主探究形成概念
(1)如果这家公司想招一名综合能力较强的翻译,我们录取的是甲
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
(2)如果这家公司想招一名笔译能力较强的翻译,按2:1:3:4的比例确定,我们录取的是 乙
这是为什么呢?
能否把这种加权平均数的计算方法推广到一般吗?
加权平均数的概念:
,...,
叫做这 个数的加权平均数。
n
2
w
,
1
w
w
n
,...,
,
2
1
的权分别是
个数
若
x
x
x
n
n
则
...
...
2
1
2
2
1
1
w
w
w
w
x
w
x
w
x
n
n
n
+
+
+
+
+
+
=
85×2+78×1+85×3+75×4
2+1+3+4
73×2+80×1+82×3+83×4
2+1+3+4
辨析
算术平均数与加权平均数的区别与联系:
(2) 在实际问题中,各项权不相等时,计算平均数时
就要采用加权平均数,当各项权相等时,计算平均数
就要采用算术平均数。
(1) 算术平均数是加权平均数的一种特殊情况
(它特殊在各项的权相等)
理解新知,巩固加深
(3)如果这家公司想招一名口语能力较强的翻译,应该侧重什么成绩?
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:甲的成绩为
85×3+78×3+85×2+73×2
3+3+2+2
=
78.9
乙的成绩为
73×3+80×3+82×2+83×2
3+3+2+2
=
80.5
显然甲的成绩比甲高,应该录取甲.
若听、说、读、写的成绩按照3:3:2:2的比确定,则应该录取谁?
如何设置能够体现听、说、读、写所占的比重有所差别呢?
自主探究形成概念
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
(2)如果这家公司想招一名笔译能力较强的翻译,按2:1:3:4的比例确定,我们录取的是 乙
大家能体会到权的作用吗
(3)如果这家公司想招一名口语能力较强的翻译,按3:3:2:2的比例确定,我们录取的是 甲
例2 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
思考(1)你认为在计算选手的综合成绩时侧重于哪个方面的成绩?三项成绩的权分别是多少?此时的权是以什么形式表现的?
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考(2)利用加权平均数公式你能求出A、B的综合成绩,决出两人的名次吗?
认真思考,一定能回答正确的。
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
思考:同学们观察表格中两名选手的单项成绩,你发现什么了?为什么他们的最后得分不同?从中你能体会到权的作用吗?
选手A的95分是演讲能力,B的95分是演讲内容,而根据题意可知,演讲内容所占的权重比演讲能力所占的权重大,所以A的95分就不如B的95分在综合成绩中占的分值大.在此更能显示出“权”的重要性.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
你真正理解了吗?
原题再现
我校初二年级为迎接5月份中考微机考试,上周进行微机模拟考试,现随机抽取我班10名同学的考试成绩,分值如下:
7 7 8 8 9 10 9 8 9 8
请同学们计算这10名同学的平均成绩。
7×2+8×4+9×3+10×1
2+4+3+1
=
8.3
总结反思
谈一谈本节课你有哪些收获?
你学会了哪些知识?
理解了哪个字的含义?
还从这节课的学习中悟到了哪些数学思想?
能否把这种加权平均数的计算方法推广到一般吗?
加权平均数的概念:
,...,
叫做这 个数的加权平均数。
n
2
w
,
1
w
w
n
,...,
,
2
1
的权分别是
个数
若
x
x
x
n
n
则
...
...
2
1
2
2
1
1
w
w
w
w
x
w
x
w
x
n
n
n
+
+
+
+
+
+
=
85×2+78×1+85×3+75×4
2+1+3+4
73×2+80×1+82×3+83×4
2+1+3+4
表格所示我校初二年级本次期中考试各班数学成绩的平均分,请同学们求我校这次数学考试的平均成绩
班级
1
2
3
4
参考人
40
42
45
30
平均分
81
80
82
79
仔细完成哦
当堂检验
课后练习1. 2
自主探究形成概念
例如:听、说、读、写成绩按2:1:3:4的比例确定,计算两名应试者的平均成绩(百分制)。从他们的成绩看,应该录取谁?
应聘者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
解:甲的成绩为
85×2+83×1+78×3+75×4
2+1+3+4
=
80.4
乙的成绩为
73×2+80×1+82×3+73×4
2+1+3+4
=
79.5
显然乙的成绩比甲高,应该录取乙.
人教版初中数学八年级下 平均数
应试者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
思考(1)这家公司在招聘英文翻译时,对甲乙两名应试者进行了哪几方面的英语水平测试?成绩分别是多少?
思考(2)招口语能力较强的翻译,“听、说、读、写成绩按照3∶3∶2∶2的比确定”,说明公司侧重于哪几个方面的成绩?
思考(3)计算两名候选人的平均成绩实际上就是求两人听、说、读、写四项成绩的加权平均数,那么它们的权分别是什么?
认真思考,你一定行的.
加权平均数的意义
在一组数据中,由于每个数据的权不同,所以计算平均数时,用加权平均数,才符合实际.
数据的权的意义
数据的权能够反映数据的相对“重要程度”.
权的三种表现形式
1、直接以数据形式给出;
2、比例形式给出;
3、百分数形式给出.
