人教版七年级数学下册 7.1 平面直角坐标系 同步测试题(Word版 含答案)
文档属性
| 名称 | 人教版七年级数学下册 7.1 平面直角坐标系 同步测试题(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 377.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 17:56:27 | ||
图片预览


文档简介
12293600110617001231900007.1 平面直角坐标系 同步测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
1. 下列说法中,正确的是(? ? ? ? )
A.点P(3,?2)到x轴的距离是3
B.在平面直角坐标系中,点(2,?-3)和点(-2,?3)表示同一个点
C.若y=0,则点M(x,?y)在y轴上
D.在平面直角坐标系中,第三象限内点的横坐标与纵坐标同号
?
2. 平面直角坐标系中,下列各点中,在x轴上的点是( )
A.(2,?0) B.(-2,?3) C.(0,?3) D.(1,?-3)
?
3. 小丽、小华的位置如图(横为排,竖为列),小丽在第5排第6列,则小华在(? ? ? ? )
A.第6排第3列 B.第6排第2列 C.第5排第3列 D.第5排第2列
?
4. 在平面直角坐标系中,若点P坐标为(2,?-3),则它位于第几象限( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
?
5. 已知一次函数y=(2m+1)x+m-3的图像不经过第二象限,则m的取值范围是(? ? ? ? )
A.B.
C.D.
?
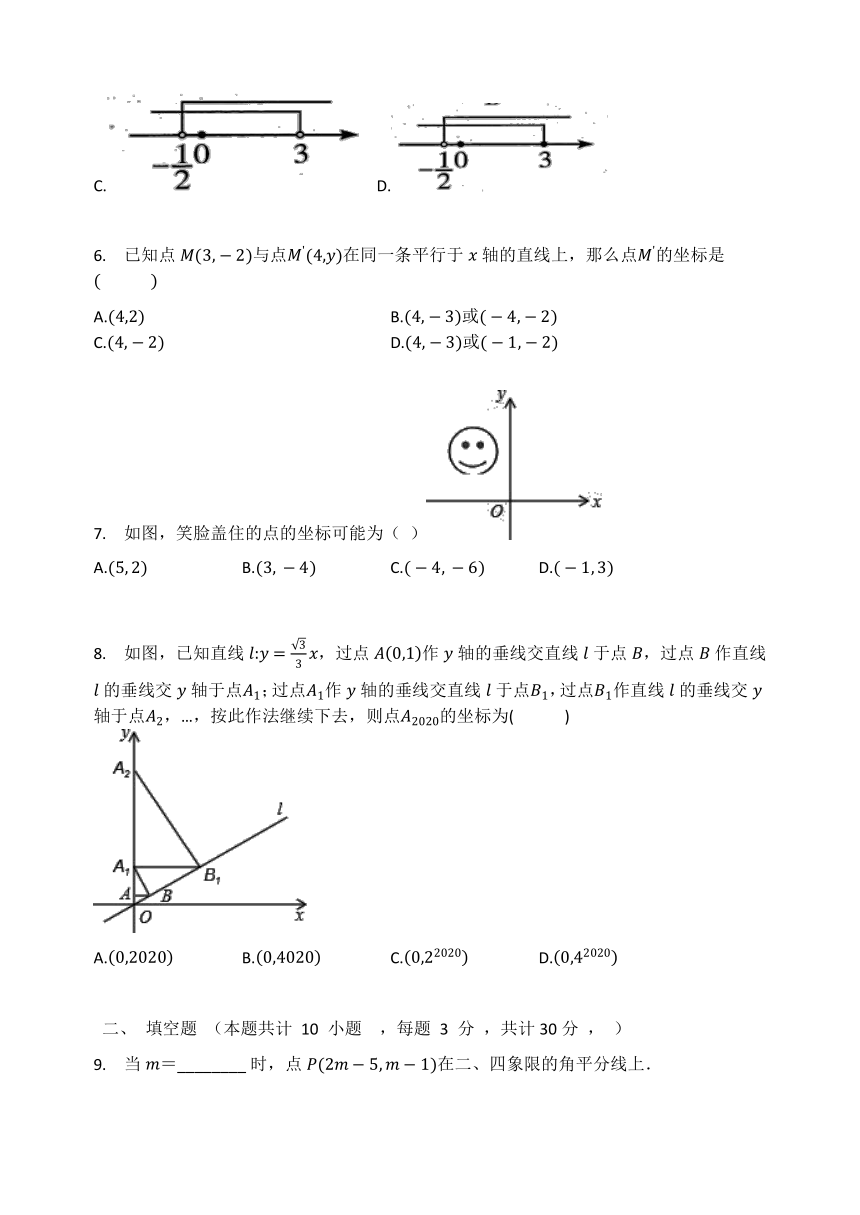
6. 已知点M(3,-2)与点M'(4,y)在同一条平行于x轴的直线上,那么点M'的坐标是(? ? ? ? )
A.(4,2) B.(4,-3)或(-4,-2)
C.(4,-2) D.(4,-3)或(-1,-2)
?
7. 如图,笑脸盖住的点的坐标可能为( )
A.(5,?2) B.(3,?-4) C.(-4,?-6) D.(-1,?3)
?
8. 如图,已知直线l:y=33x,过点A0,1作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,…,按此作法继续下去,则点A2020的坐标为(? ? ? ? )
A.0,2020 B.0,4020 C.0,22020 D.0,42020
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
9. 当m=________?时,点P(2m-5,?m-1)在二、四象限的角平分线上.
?
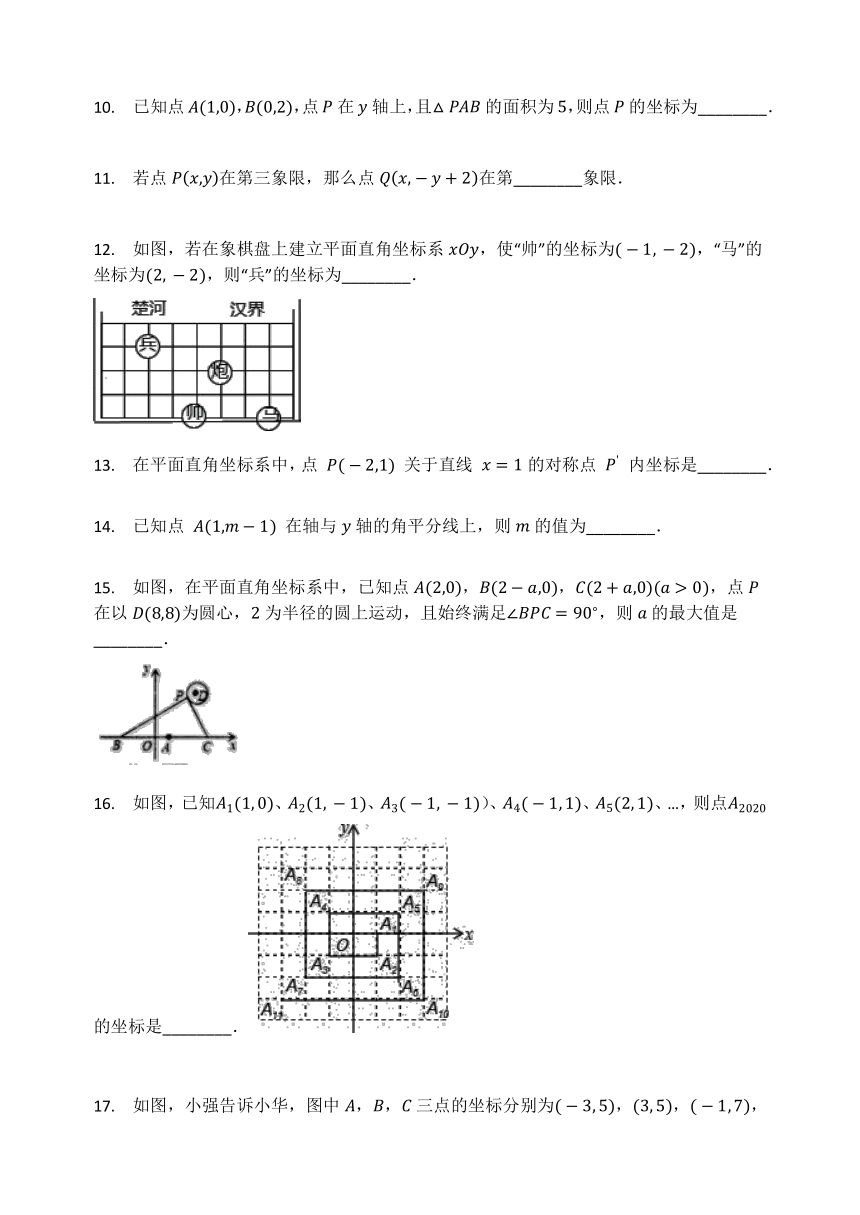
10. 已知点A(1,0),B(0,2),点P在y轴上,且△PAB的面积为5,则点P的坐标为________.
?
11. 若点Px,y在第三象限,那么点Qx,-y+2在第________象限.
?
12. 如图,若在象棋盘上建立平面直角坐标系xOy,使“帅”的坐标为(-1,?-2),“马”的坐标为(2,?-2),则“兵”的坐标为________.
13. 在平面直角坐标系中,点 P(-2,1) 关于直线 x=1的对称点 P' 内坐标是________.
?
14. 已知点 A(1,m-1) 在轴与y轴的角平分线上,则m的值为________.
?
15. 如图,在平面直角坐标系中,已知点A(2,0),B(2-a,0),C(2+a,0)(a>0),点P在以D(8,8)为圆心,2为半径的圆上运动,且始终满足∠BPC=90?,则a的最大值是________.
?
16. 如图,已知A1(1,?0)、A2(1,?-1)、A3(-1,?-1))、A4(-1,?1)、A5(2,?1)、…,则点A2020的坐标是________.
?
17. 如图,小强告诉小华,图中A,B,C三点的坐标分别为(-3,?5),(3,?5),(-1,?7),小华一下就说出了点D在同一坐标系中的坐标为________.
?
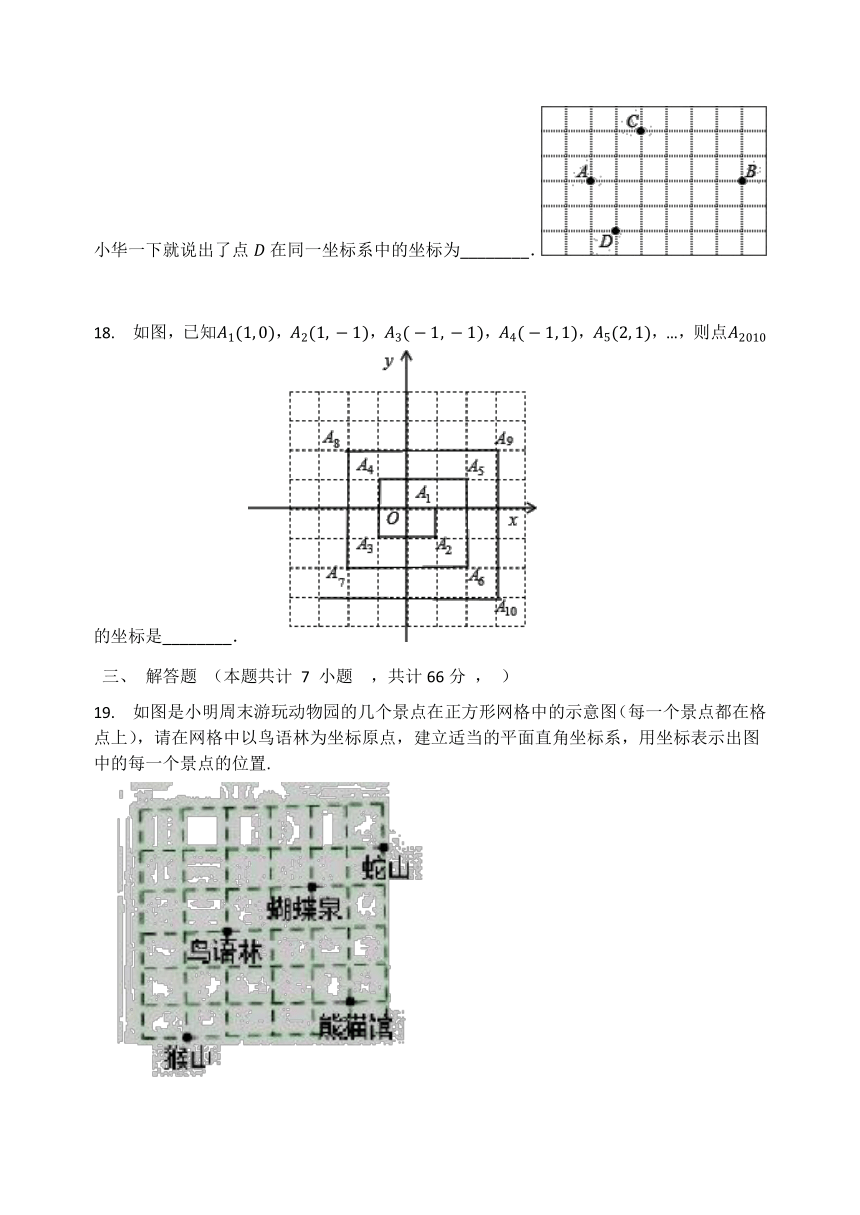
18. 如图,已知A1(1,?0),A2(1,?-1),A3(-1,?-1),A4(-1,?1),A5(2,?1),…,则点A2010的坐标是________.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 如图是小明周末游玩动物园的几个景点在正方形网格中的示意图(每一个景点都在格点上),请在网格中以鸟语林为坐标原点,建立适当的平面直角坐标系,用坐标表示出图中的每一个景点的位置.
?
20. 如图,方格纸中的每个小方格都是边长为1个单位的正方形.在建立平面直角坐标系后,△ABC的顶点在格点上,且点A的坐标为(-2,-1),点B的坐标为(4,-1),点C的坐标为(1,3),将△ABC向右平移4个单位,再向上平移3个单位后得到△A1B1C1.
(1)在图中画出△A1B1C1.
(2)写出点A1,B1,C1的坐标.
(3)写出△A1B1C1的面积.
?
21. 已知点A(-2,?8),B(-9,?6),现将A点向右平移2个单位长度,再向下平移8个单位长度得到点D,C点在x轴负半轴上且距离y轴12个单位长度.
1点D的坐标为________;
2请在右边的平面直角坐标系中画出四边形ABCD;
3四边形ABCD的面积为________.
?
22. 如图,正方形ABCD的边长为4,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.
(1)试写出正方形四个顶点的坐标;
(2)从中你发现了什么规律,请举例说明(写出一个即可).
?
23. 观察以下等式:
(-1)×12=(-1)+12,
(-2)×23=(-2)+23,
(-3)×34=(-3)+34,
(-4)×45=(-4)+45,
(1)依此规律进行下去,第5个等式为________,猜想第n个等式为________(n为正整数);
(2)请利用分式的运算证明你的猜想.
?
24. 已知:点P(2m+4,?m-1).试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过A(2,?-3)点,且与x轴平行的直线上.
?
参考答案
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.
【答案】
D
【解答】
解:A、点P(3,?2)到x轴的距离为2,故此选项错误;
B、在平面直角坐标系内,点(2,?-3)和点(-2,?3)表示不同的点,故此选项错误;
C、若y=0,则点M(x,?y)在x轴上,故此选项错误;
D、在平面直角坐标系中,第三象限内点的横坐标与纵坐标同号,故此选项正确.
故选D.
2.
【答案】
A
【解答】
解:∵ 各选项中,只有(2,?0)的纵坐标为0,
∴ 在x轴上的点是(2,?0).
故选A.
3.
【答案】
A
【解答】
解:因为小丽在第5排第6列,所以小华在第6排第3列.
故选A.
4.
【答案】
D
【解答】
解:点P坐标为(2,?-3),则它位于第四象限,
故选:D.
5.
【答案】
D
【解答】
解:由于一次函数y=(2m+1)x+m-3的图象不经过第二象限,
故2m+1>0,m-3≤0,
解得 -12在数轴上表示为:
故选D.
6.
【答案】
C
【解答】
解:因为两点在同一条平行于x轴的直线上,
所以两点的纵坐标相等,
所以y=-2,
故选C.
7.
【答案】
D
【解答】
解:笑脸位于第二象限,故D符合题意;
故选:D.
8.
【答案】
D
【解答】
解:∵ 直线l的解析式为:y=33x,
∴ l与x轴的夹角为30?,
∵ AB?//?x轴,
∴ ∠ABO=30?,
∵ OA=1,
∴ AB=3,
∵ A1B⊥l,
∴ ∠ABA1=60?,
∴ AA1=3,
∴ A1(0,?4),
同理可得A2(0,?16),
…,
∴ A2020纵坐标为:42020,
∴ A2020(0,?42020).
故选D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
9.
【答案】
2
【解答】
∵ 点P(2m-5,?m-1)在第二、四象限的夹角角平分线上,
∴ 2m-5+(m-1)=0,
解得:m=2.
10.
【答案】
(0,-8)或(0,12)
【解答】
解:∵ A(1,0),B(0,2),
∴ S△PAB=12BP×1=5
解得BP=10,
若点P在点B的上边,则OP=2+10=12,
此时,点P的坐标为(0,12),
若点P在点B的下边,则OP=10-2=8,
此时,点P的坐标为(0,-8).
故答案为(0,-8)或(0,12).
B7
11.
【答案】
二
【解答】
解:∵ P(x,y)在第三象限,
∴ x<0,y<0,
∴ -y+2>0,
∴ Q(x,-y+2)在第二象限.
故答案为:二.
12.
【答案】
(-3,?1)
【解答】
解:如图所示,建立直角坐标系,
所以“兵”的坐标为:(-3,?1).
故答案为:(-3,?1).
13.
【答案】
(4,1)
【解答】
此题暂无解答
14.
【答案】
0或2
【解答】
此题暂无解答
15.
【答案】
【解答】
此题暂无解答
16.
【答案】
(-504,?-504)
【解答】
解:∵ A1(1,?0)、A2(1,?-1)、A3(-1,?-1))、A4(-1,?1)、
A5(2,?1)、A6(2,?-2)、A7(-2,?-2)、A8(-2,?2)…,
通过观察可得数字是4的倍数的点在第二象限,4的倍数余1的点在第一象限,4的倍数余2的点在第四象限,4的倍数余3的点在第三象限,
∵ 2015÷4=503...3,
∴ 点A2015在第三象限,且转动了503圈以后,在第504圈上,
∴ A2015的坐标为(-504,?-504),
故答案为:(-504,?-504).
17.
【答案】
(-2,?3)
【解答】
解:∵ 点D在点A(-3,?5),右边一个单位,下边2个单位,
∴ 点D的横坐标为-3+1=-2,
纵坐标为5-2=3,
∴ 点D的坐标为(-2,?3).
故答案为:(-2,?3).
18.
【答案】
(503,?-503)
【解答】
解:易得4的整数倍的各点如A4,A8,A12等点在第二象限,
∵ 2010÷4=502...2;
∴ A2010的坐标在第四象限,
横坐标为(2010-2)÷4+1=503;纵坐标为-503,
∴ 点A2010的坐标是(503,?-503).
故答案为:(503,?-503).
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:如图:
以鸟语林为坐标原点建立平面直角坐标系,则
鸟语林(0,0),蝴蝶泉(2,1),蛇山(4,2),猴山(-1,-3),熊猫馆(3,-2).
【解答】
解:如图:
以鸟语林为坐标原点建立平面直角坐标系,则
鸟语林(0,0),蝴蝶泉(2,1),蛇山(4,2),猴山(-1,-3),熊猫馆(3,-2).
20.
【答案】
解:(1)如图:
(2)A1(2,2),B1(8,2),C1(5,6).
(3)S△A1B1C1=12×6×4=12.
【解答】
解:(1)如图:
(2)A1(2,2),B1(8,2),C1(5,6).
(3)S△A1B1C1=12×6×4=12.
21.
【答案】
(0,?0)
2如图所示;
66
【解答】
解:1由题意可知,A点的横坐标先加2,纵坐标再减8,故D(0,?0);
故答案为:(0,0).
2如图所示;
3如图:
S四边形ABCD=S△BCE+S△AFD+S梯形BEFA
=12×3×6+12×2×8+12×(6+8)×7
=9+8+49
=66.
故答案为:66.
22.
【答案】
解:(1)设正方形与y轴的交点分别为E,F(F点在E点下方),
与x轴交于M、N点(N点在M点右方),如图1所示:
∵ 正方形ABCD的边长为4,且中心为坐标原点,
∴ AE=ED=DN=NC=CF=FB=BM=MA=2,
∴ 点A的坐标为(-2,?2),点B的坐标为(-2,?-2),点C的坐标为(2,?-2),点D的坐标为(2,?2).
(2)B,D点的横(纵)坐标互为相反数.
连接AC,BD,如图2所示:
∵ 坐标原点为正方形的中心,且正方形的对角线互相平分,
∴ 点O为线段BD的中点,
∴ B,D点的横(纵)坐标互为相反数.
【解答】
解:(1)设正方形与y轴的交点分别为E,F(F点在E点下方),
与x轴交于M、N点(N点在M点右方),如图1所示:
∵ 正方形ABCD的边长为4,且中心为坐标原点,
∴ AE=ED=DN=NC=CF=FB=BM=MA=2,
∴ 点A的坐标为(-2,?2),点B的坐标为(-2,?-2),点C的坐标为(2,?-2),点D的坐标为(2,?2).
(2)B,D点的横(纵)坐标互为相反数.
连接AC,BD,如图2所示:
∵ 坐标原点为正方形的中心,且正方形的对角线互相平分,
∴ 点O为线段BD的中点,
∴ B,D点的横(纵)坐标互为相反数.
23.
【答案】
(-5)×56=(-5)+56,(-n)?nn+1=(-n)+nn+1
+56;(-n)?nn+1=(-n)+nn+1;
【解答】
根据题意得:第5个等式为(-5)×56=(-5)+56,第n个等式为(-n)?nn+1=(-n)+nn+1;
故答案为:(-5)×56=(-5)+56;(-n)?nn+1=(-n)+nn+1;
左边=-n2n+1,右边=-n(n+1)+nn+1=-n2-n+nn+1=-n2n+1,
则左边=右边,即(-n)?nn+1=(-n)+nn+1.
24.
【答案】
解:(1)令2m+4=0,解得m=-2,所以P点的坐标为(0,?-3);
(2)令m-1=0,解得m=1,所以P点的坐标为(6,?0);
(3)令m-1=(2m+4)+3,解得m=-8,所以P点的坐标为(-12,?-9);
(4)令m-1=-3,解得m=-2.所以P点的坐标为(0,?-3).
【解答】
解:(1)令2m+4=0,解得m=-2,所以P点的坐标为(0,?-3);
(2)令m-1=0,解得m=1,所以P点的坐标为(6,?0);
(3)令m-1=(2m+4)+3,解得m=-8,所以P点的坐标为(-12,?-9);
(4)令m-1=-3,解得m=-2.所以P点的坐标为(0,?-3).
(满分120分;时间:120分钟)
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
1. 下列说法中,正确的是(? ? ? ? )
A.点P(3,?2)到x轴的距离是3
B.在平面直角坐标系中,点(2,?-3)和点(-2,?3)表示同一个点
C.若y=0,则点M(x,?y)在y轴上
D.在平面直角坐标系中,第三象限内点的横坐标与纵坐标同号
?
2. 平面直角坐标系中,下列各点中,在x轴上的点是( )
A.(2,?0) B.(-2,?3) C.(0,?3) D.(1,?-3)
?
3. 小丽、小华的位置如图(横为排,竖为列),小丽在第5排第6列,则小华在(? ? ? ? )
A.第6排第3列 B.第6排第2列 C.第5排第3列 D.第5排第2列
?
4. 在平面直角坐标系中,若点P坐标为(2,?-3),则它位于第几象限( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
?
5. 已知一次函数y=(2m+1)x+m-3的图像不经过第二象限,则m的取值范围是(? ? ? ? )
A.B.
C.D.
?
6. 已知点M(3,-2)与点M'(4,y)在同一条平行于x轴的直线上,那么点M'的坐标是(? ? ? ? )
A.(4,2) B.(4,-3)或(-4,-2)
C.(4,-2) D.(4,-3)或(-1,-2)
?
7. 如图,笑脸盖住的点的坐标可能为( )
A.(5,?2) B.(3,?-4) C.(-4,?-6) D.(-1,?3)
?
8. 如图,已知直线l:y=33x,过点A0,1作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,…,按此作法继续下去,则点A2020的坐标为(? ? ? ? )
A.0,2020 B.0,4020 C.0,22020 D.0,42020
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
9. 当m=________?时,点P(2m-5,?m-1)在二、四象限的角平分线上.
?
10. 已知点A(1,0),B(0,2),点P在y轴上,且△PAB的面积为5,则点P的坐标为________.
?
11. 若点Px,y在第三象限,那么点Qx,-y+2在第________象限.
?
12. 如图,若在象棋盘上建立平面直角坐标系xOy,使“帅”的坐标为(-1,?-2),“马”的坐标为(2,?-2),则“兵”的坐标为________.
13. 在平面直角坐标系中,点 P(-2,1) 关于直线 x=1的对称点 P' 内坐标是________.
?
14. 已知点 A(1,m-1) 在轴与y轴的角平分线上,则m的值为________.
?
15. 如图,在平面直角坐标系中,已知点A(2,0),B(2-a,0),C(2+a,0)(a>0),点P在以D(8,8)为圆心,2为半径的圆上运动,且始终满足∠BPC=90?,则a的最大值是________.
?
16. 如图,已知A1(1,?0)、A2(1,?-1)、A3(-1,?-1))、A4(-1,?1)、A5(2,?1)、…,则点A2020的坐标是________.
?
17. 如图,小强告诉小华,图中A,B,C三点的坐标分别为(-3,?5),(3,?5),(-1,?7),小华一下就说出了点D在同一坐标系中的坐标为________.
?
18. 如图,已知A1(1,?0),A2(1,?-1),A3(-1,?-1),A4(-1,?1),A5(2,?1),…,则点A2010的坐标是________.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 如图是小明周末游玩动物园的几个景点在正方形网格中的示意图(每一个景点都在格点上),请在网格中以鸟语林为坐标原点,建立适当的平面直角坐标系,用坐标表示出图中的每一个景点的位置.
?
20. 如图,方格纸中的每个小方格都是边长为1个单位的正方形.在建立平面直角坐标系后,△ABC的顶点在格点上,且点A的坐标为(-2,-1),点B的坐标为(4,-1),点C的坐标为(1,3),将△ABC向右平移4个单位,再向上平移3个单位后得到△A1B1C1.
(1)在图中画出△A1B1C1.
(2)写出点A1,B1,C1的坐标.
(3)写出△A1B1C1的面积.
?
21. 已知点A(-2,?8),B(-9,?6),现将A点向右平移2个单位长度,再向下平移8个单位长度得到点D,C点在x轴负半轴上且距离y轴12个单位长度.
1点D的坐标为________;
2请在右边的平面直角坐标系中画出四边形ABCD;
3四边形ABCD的面积为________.
?
22. 如图,正方形ABCD的边长为4,过它的中心建立平面直角坐标系(中心在原点上),各边和坐标轴平行或垂直.
(1)试写出正方形四个顶点的坐标;
(2)从中你发现了什么规律,请举例说明(写出一个即可).
?
23. 观察以下等式:
(-1)×12=(-1)+12,
(-2)×23=(-2)+23,
(-3)×34=(-3)+34,
(-4)×45=(-4)+45,
(1)依此规律进行下去,第5个等式为________,猜想第n个等式为________(n为正整数);
(2)请利用分式的运算证明你的猜想.
?
24. 已知:点P(2m+4,?m-1).试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过A(2,?-3)点,且与x轴平行的直线上.
?
参考答案
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.
【答案】
D
【解答】
解:A、点P(3,?2)到x轴的距离为2,故此选项错误;
B、在平面直角坐标系内,点(2,?-3)和点(-2,?3)表示不同的点,故此选项错误;
C、若y=0,则点M(x,?y)在x轴上,故此选项错误;
D、在平面直角坐标系中,第三象限内点的横坐标与纵坐标同号,故此选项正确.
故选D.
2.
【答案】
A
【解答】
解:∵ 各选项中,只有(2,?0)的纵坐标为0,
∴ 在x轴上的点是(2,?0).
故选A.
3.
【答案】
A
【解答】
解:因为小丽在第5排第6列,所以小华在第6排第3列.
故选A.
4.
【答案】
D
【解答】
解:点P坐标为(2,?-3),则它位于第四象限,
故选:D.
5.
【答案】
D
【解答】
解:由于一次函数y=(2m+1)x+m-3的图象不经过第二象限,
故2m+1>0,m-3≤0,
解得 -12
故选D.
6.
【答案】
C
【解答】
解:因为两点在同一条平行于x轴的直线上,
所以两点的纵坐标相等,
所以y=-2,
故选C.
7.
【答案】
D
【解答】
解:笑脸位于第二象限,故D符合题意;
故选:D.
8.
【答案】
D
【解答】
解:∵ 直线l的解析式为:y=33x,
∴ l与x轴的夹角为30?,
∵ AB?//?x轴,
∴ ∠ABO=30?,
∵ OA=1,
∴ AB=3,
∵ A1B⊥l,
∴ ∠ABA1=60?,
∴ AA1=3,
∴ A1(0,?4),
同理可得A2(0,?16),
…,
∴ A2020纵坐标为:42020,
∴ A2020(0,?42020).
故选D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
9.
【答案】
2
【解答】
∵ 点P(2m-5,?m-1)在第二、四象限的夹角角平分线上,
∴ 2m-5+(m-1)=0,
解得:m=2.
10.
【答案】
(0,-8)或(0,12)
【解答】
解:∵ A(1,0),B(0,2),
∴ S△PAB=12BP×1=5
解得BP=10,
若点P在点B的上边,则OP=2+10=12,
此时,点P的坐标为(0,12),
若点P在点B的下边,则OP=10-2=8,
此时,点P的坐标为(0,-8).
故答案为(0,-8)或(0,12).
B7
11.
【答案】
二
【解答】
解:∵ P(x,y)在第三象限,
∴ x<0,y<0,
∴ -y+2>0,
∴ Q(x,-y+2)在第二象限.
故答案为:二.
12.
【答案】
(-3,?1)
【解答】
解:如图所示,建立直角坐标系,
所以“兵”的坐标为:(-3,?1).
故答案为:(-3,?1).
13.
【答案】
(4,1)
【解答】
此题暂无解答
14.
【答案】
0或2
【解答】
此题暂无解答
15.
【答案】
【解答】
此题暂无解答
16.
【答案】
(-504,?-504)
【解答】
解:∵ A1(1,?0)、A2(1,?-1)、A3(-1,?-1))、A4(-1,?1)、
A5(2,?1)、A6(2,?-2)、A7(-2,?-2)、A8(-2,?2)…,
通过观察可得数字是4的倍数的点在第二象限,4的倍数余1的点在第一象限,4的倍数余2的点在第四象限,4的倍数余3的点在第三象限,
∵ 2015÷4=503...3,
∴ 点A2015在第三象限,且转动了503圈以后,在第504圈上,
∴ A2015的坐标为(-504,?-504),
故答案为:(-504,?-504).
17.
【答案】
(-2,?3)
【解答】
解:∵ 点D在点A(-3,?5),右边一个单位,下边2个单位,
∴ 点D的横坐标为-3+1=-2,
纵坐标为5-2=3,
∴ 点D的坐标为(-2,?3).
故答案为:(-2,?3).
18.
【答案】
(503,?-503)
【解答】
解:易得4的整数倍的各点如A4,A8,A12等点在第二象限,
∵ 2010÷4=502...2;
∴ A2010的坐标在第四象限,
横坐标为(2010-2)÷4+1=503;纵坐标为-503,
∴ 点A2010的坐标是(503,?-503).
故答案为:(503,?-503).
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:如图:
以鸟语林为坐标原点建立平面直角坐标系,则
鸟语林(0,0),蝴蝶泉(2,1),蛇山(4,2),猴山(-1,-3),熊猫馆(3,-2).
【解答】
解:如图:
以鸟语林为坐标原点建立平面直角坐标系,则
鸟语林(0,0),蝴蝶泉(2,1),蛇山(4,2),猴山(-1,-3),熊猫馆(3,-2).
20.
【答案】
解:(1)如图:
(2)A1(2,2),B1(8,2),C1(5,6).
(3)S△A1B1C1=12×6×4=12.
【解答】
解:(1)如图:
(2)A1(2,2),B1(8,2),C1(5,6).
(3)S△A1B1C1=12×6×4=12.
21.
【答案】
(0,?0)
2如图所示;
66
【解答】
解:1由题意可知,A点的横坐标先加2,纵坐标再减8,故D(0,?0);
故答案为:(0,0).
2如图所示;
3如图:
S四边形ABCD=S△BCE+S△AFD+S梯形BEFA
=12×3×6+12×2×8+12×(6+8)×7
=9+8+49
=66.
故答案为:66.
22.
【答案】
解:(1)设正方形与y轴的交点分别为E,F(F点在E点下方),
与x轴交于M、N点(N点在M点右方),如图1所示:
∵ 正方形ABCD的边长为4,且中心为坐标原点,
∴ AE=ED=DN=NC=CF=FB=BM=MA=2,
∴ 点A的坐标为(-2,?2),点B的坐标为(-2,?-2),点C的坐标为(2,?-2),点D的坐标为(2,?2).
(2)B,D点的横(纵)坐标互为相反数.
连接AC,BD,如图2所示:
∵ 坐标原点为正方形的中心,且正方形的对角线互相平分,
∴ 点O为线段BD的中点,
∴ B,D点的横(纵)坐标互为相反数.
【解答】
解:(1)设正方形与y轴的交点分别为E,F(F点在E点下方),
与x轴交于M、N点(N点在M点右方),如图1所示:
∵ 正方形ABCD的边长为4,且中心为坐标原点,
∴ AE=ED=DN=NC=CF=FB=BM=MA=2,
∴ 点A的坐标为(-2,?2),点B的坐标为(-2,?-2),点C的坐标为(2,?-2),点D的坐标为(2,?2).
(2)B,D点的横(纵)坐标互为相反数.
连接AC,BD,如图2所示:
∵ 坐标原点为正方形的中心,且正方形的对角线互相平分,
∴ 点O为线段BD的中点,
∴ B,D点的横(纵)坐标互为相反数.
23.
【答案】
(-5)×56=(-5)+56,(-n)?nn+1=(-n)+nn+1
+56;(-n)?nn+1=(-n)+nn+1;
【解答】
根据题意得:第5个等式为(-5)×56=(-5)+56,第n个等式为(-n)?nn+1=(-n)+nn+1;
故答案为:(-5)×56=(-5)+56;(-n)?nn+1=(-n)+nn+1;
左边=-n2n+1,右边=-n(n+1)+nn+1=-n2-n+nn+1=-n2n+1,
则左边=右边,即(-n)?nn+1=(-n)+nn+1.
24.
【答案】
解:(1)令2m+4=0,解得m=-2,所以P点的坐标为(0,?-3);
(2)令m-1=0,解得m=1,所以P点的坐标为(6,?0);
(3)令m-1=(2m+4)+3,解得m=-8,所以P点的坐标为(-12,?-9);
(4)令m-1=-3,解得m=-2.所以P点的坐标为(0,?-3).
【解答】
解:(1)令2m+4=0,解得m=-2,所以P点的坐标为(0,?-3);
(2)令m-1=0,解得m=1,所以P点的坐标为(6,?0);
(3)令m-1=(2m+4)+3,解得m=-8,所以P点的坐标为(-12,?-9);
(4)令m-1=-3,解得m=-2.所以P点的坐标为(0,?-3).
