湖南省澧县张公庙中学2020年秋湘教版八年级数学上册期末复习试卷(二)(Word版 含答案)
文档属性
| 名称 | 湖南省澧县张公庙中学2020年秋湘教版八年级数学上册期末复习试卷(二)(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 00:00:00 | ||
图片预览



文档简介
湖南省澧县张公庙中学2020年(秋季)八年级数学上册期末复习试卷(二)与简答
一.选择题(共8小题,每小题3分,共24分)
1.下列分式中,属于最简分式的是
A. B. C. D.
2.花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,那么0.000037毫克可用科学记数法表示为
A.毫克 B.毫克
C.毫克 D.毫克
3.如图,是关于的不等式的解集,则的取值是
A. B. C. D.
4.已知,则下列不等式不成立的是
A. B. C. D.
5.的算术平方根为
A.9 B. C.3 D.
6.若,则的取值范围是
A. B. C. D.
7.已知等腰三角形的两边满足,则此三角形的周长为
A.12 B.15 C.12或15 D.不能确定
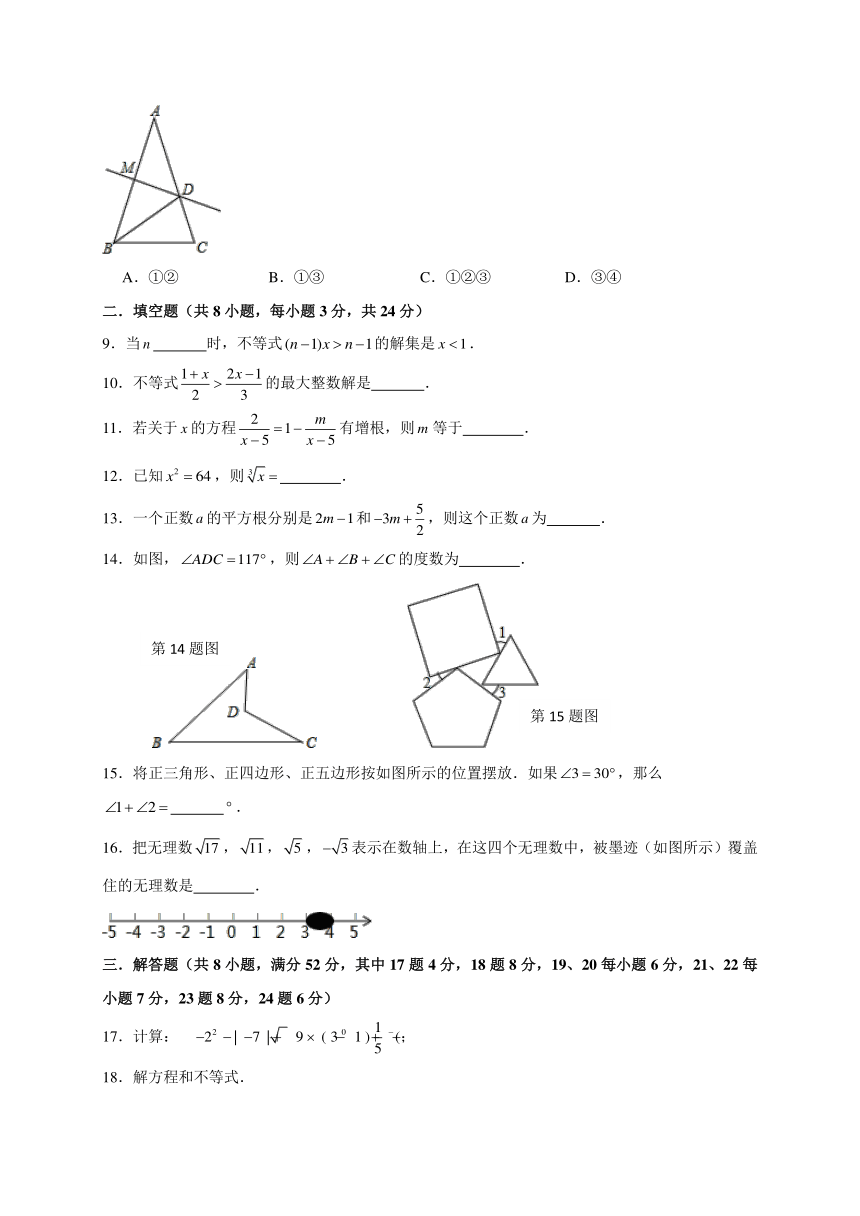
8.如图,已知,,的垂直平分线交于,于,以下结论:①是等腰三角形;②射线是的角平分线;③的周长;④.正确的有
A.①② B.①③ C.①②③ D.③④
二.填空题(共8小题,每小题3分,共24分)
9.当 时,不等式的解集是.
10.不等式的最大整数解是 .
11.若关于的方程有增根,则等于 .
12.已知,则 .
13.一个正数的平方根分别是和,则这个正数为 .
14.如图,,则的度数为 .
15.将正三角形、正四边形、正五边形按如图所示的位置摆放.如果,那么
.
16.把无理数,,,表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是 .
三.解答题(共8小题,满分52分,其中17题4分,18题8分,19、20每小题6分,21、22每小题7分,23题8分,24题6分)
17.计算: ;
18.解方程和不等式.
(1);
(2).
19.先化简:; 再在不等式组的整数解中选取一个合适的解作为的取值,代入求值.
20.先化简,再求值:,其中.
如图是小亮和小芳的解答过程.
(1) 的解法是错误的;
错误的原因在于未能正确地运用二次根式的性质: ;
(2)先化简,再求值:,其中.
21.倡导健康生活推进全民健身,某社区去年购进,两种健身器材若干件,经了解,种健身器材的单价是种健身器材的1.5倍,用7200元购买种健身器材比用5400元购买种健身器材多10件.
(1),两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进,两种健身器材共50件,且费用不超过21000元,请问:种健身器材至少要购买多少件?
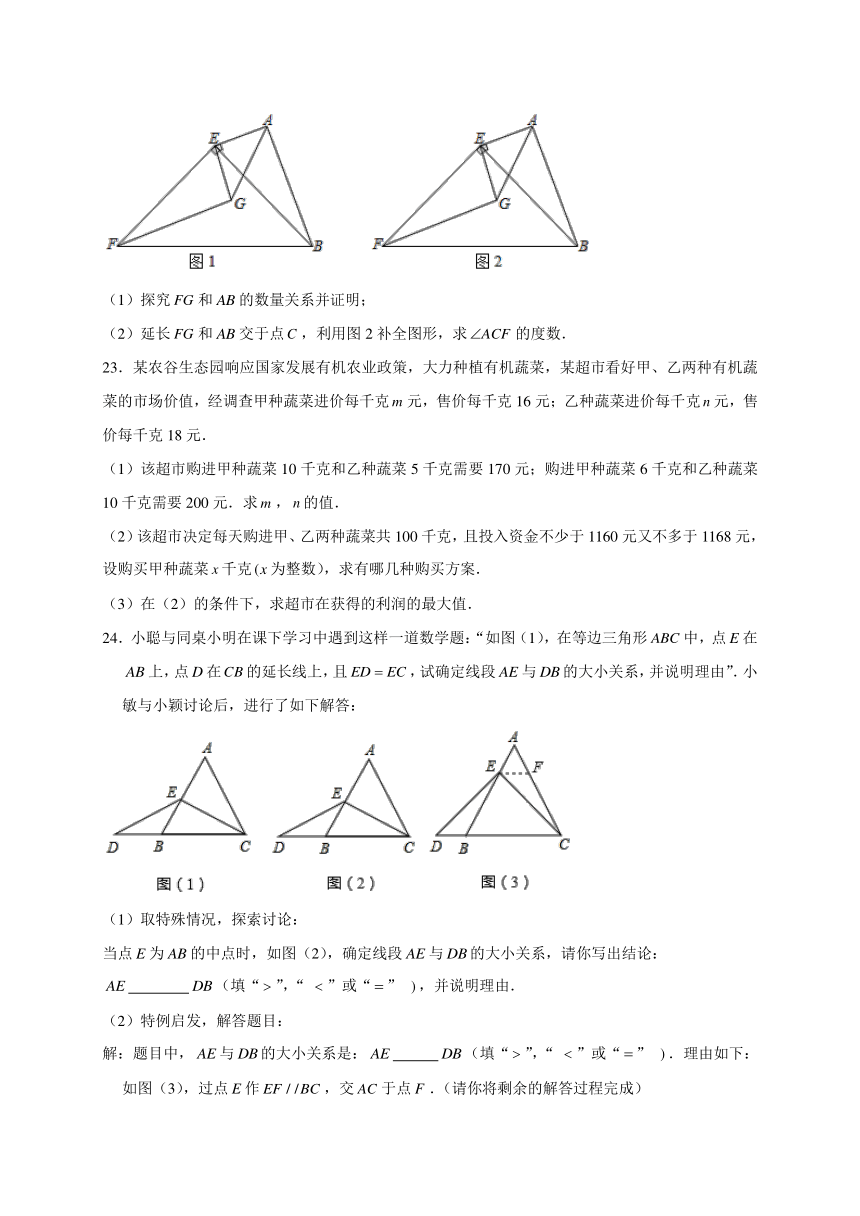
22.如图,和是等腰直角三角形.
(1)探究和的数量关系并证明;
(2)延长和交于点,利用图2补全图形,求的度数.
23.某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克元,售价每千克16元;乙种蔬菜进价每千克元,售价每千克18元.
(1)该超市购进甲种蔬菜10千克和乙种蔬菜5千克需要170元;购进甲种蔬菜6千克和乙种蔬菜10千克需要200元.求,的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜千克为整数),求有哪几种购买方案.
(3)在(2)的条件下,求超市在获得的利润的最大值.
24.小聪与同桌小明在课下学习中遇到这样一道数学题:“如图(1),在等边三角形中,点在上,点在的延长线上,且,试确定线段与的大小关系,并说明理由”.小敏与小颖讨论后,进行了如下解答:
(1)取特殊情况,探索讨论:
当点为的中点时,如图(2),确定线段与的大小关系,请你写出结论:
(填“”,“ ”或“” ,并说明理由.
(2)特例启发,解答题目:
解:题目中,与的大小关系是: (填“”,“ ”或“” .理由如下:如图(3),过点作,交于点.(请你将剩余的解答过程完成)
(3)拓展结论,设计新题:
在等边三角形中,点在直线上,点在直线上,且,若的边长为1,,则的长为 .(请你画出图形,并直接写出结果).
湖南省澧县张公庙中学2020年(秋季)八年级数学上册期末复习试卷(二)参考简答
一.选择题(共8小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
二.填空题(共8小题)
9. . 10. 4 . 11. . 12. . 13. 4 .
14. . 15. 72 . 16. .
三.解答题(共8小题)
17.计算:
(1);
(2).
【解】:(1)原式
;
(2)原式
.
18.解方程和不等式.
(1);
(2).
【解】:(1)不等式整理得:,
移项合并得:,
解得:;
(2)去分母得:,
解得:,
经检验是分式方程的解.
19.先化简:; 再在不等式组的整数解中选取一个合适的解作为的取值,代入求值.
【解】:原式
,
解不等式,得:,
解不等式,得:,
则不等式组的解集为,
其整数解有、0、1,
,
, 则原式.
20.先化简,再求值:,其中.
如图是小亮和小芳的解答过程.
(1) 的解法是错误的;
错误的原因在于未能正确地运用二次根式的性质: ;
(2)先化简,再求值:,其中.
【解】:(1)小亮的解法是错误的,
错误的原因在于未能正确地运用二次根式的性质:,
(2)原式,
,
原式.
21.倡导健康生活推进全民健身,某社区去年购进,两种健身器材若干件,经了解,种健身器材的单价是种健身器材的1.5倍,用7200元购买种健身器材比用5400元购买种健身器材多10件.
(1),两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进,两种健身器材共50件,且费用不超过21000元,请问:种健身器材至少要购买多少件?
【解】:(1)设种型号健身器材的单价为元套,种型号健身器材的单价为元套,
根据题意,可得:,
解得:,
经检验是原方程的根,
(元,
因此,,两种健身器材的单价分别是360元,540元;
(2)设购买种型号健身器材套,则购买种型号的健身器材套,
根据题意,可得:,
解得:,
因此,种型号健身器材至少购买34套.
22.如图,和是等腰直角三角形.
(1)探究和的数量关系并证明;
(2)延长和交于点,利用图2补全图形,求的度数.
【解】:(1),
理由如下:
和是等腰直角三角形,
,,,
,
即,
在和中,
, ,
;
(2)如图,即为补全的图形,
由(1)知,
,
是等腰直角三角形,
,
,
,
.
23.某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克元,售价每千克16元;乙种蔬菜进价每千克元,售价每千克18元.
(1)该超市购进甲种蔬菜10千克和乙种蔬菜5千克需要170元;购进甲种蔬菜6千克和乙种蔬菜10千克需要200元.求,的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜千克为整数),求有哪几种购买方案.
(3)在(2)的条件下,求超市在获得的利润的最大值.
【解】:(1)依题意,得:
, 解得:.
答:的值为10,的值为14.
(2)设购买甲种蔬菜千克,则购买乙种蔬菜千克,
依题意,得:, 解得:.
为正整数,
,59,60,
有3种购买方案,方案1:购买甲种蔬菜58千克,乙种蔬菜42千克;方案2:购买甲种蔬菜59千克,乙种蔬菜41千克;方案3:购买甲种蔬菜60千克,乙种蔬菜40千克.
(3)设超市获得的利润为元,则.
当时,取得最大值,最大值为.
24.小聪与同桌小明在课下学习中遇到这样一道数学题:“如图(1),在等边三角形中,点在上,点在的延长线上,且,试确定线段与的大小关系,并说明理由”.小敏与小颖讨论后,进行了如下解答:
(1)取特殊情况,探索讨论:
当点为的中点时,如图(2),确定线段与的大小关系,请你写出结论:
(填“”,“ ”或“” ,并说明理由.
(2)特例启发,解答题目:
解:题目中,与的大小关系是: (填“”,“ ”或“” .理由如下:如图(3),过点作,交于点.(请你将剩余的解答过程完成)
(3)拓展结论,设计新题:
在等边三角形中,点在直线上,点在直线上,且,若的边长为1,,则的长为 .(请你画出图形,并直接写出结果).
【解】:(1),
理由如下:,
,
三角形是等边三角形,
,
点为的中点,
,
,
,
,
,
,
(2)如图3,
为等边三角形,且,
,,,
,
,
,,
在与中,
, ,
,
, 为等边三角形,
,,
(3)如图4,
当点在的延长线上时,过点作,交的延长线于点,
则,,,,
为等边三角形,
,
,,
,而,
,,
在与中,
, ,
,
为等边三角形,
,,
;
如图5,
当点在的延长线上时,过点作,交的延长线于点,
类似上述解法,同理可证:,,
,
综上可得为:3或1.
一.选择题(共8小题,每小题3分,共24分)
1.下列分式中,属于最简分式的是
A. B. C. D.
2.花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,那么0.000037毫克可用科学记数法表示为
A.毫克 B.毫克
C.毫克 D.毫克
3.如图,是关于的不等式的解集,则的取值是
A. B. C. D.
4.已知,则下列不等式不成立的是
A. B. C. D.
5.的算术平方根为
A.9 B. C.3 D.
6.若,则的取值范围是
A. B. C. D.
7.已知等腰三角形的两边满足,则此三角形的周长为
A.12 B.15 C.12或15 D.不能确定
8.如图,已知,,的垂直平分线交于,于,以下结论:①是等腰三角形;②射线是的角平分线;③的周长;④.正确的有
A.①② B.①③ C.①②③ D.③④
二.填空题(共8小题,每小题3分,共24分)
9.当 时,不等式的解集是.
10.不等式的最大整数解是 .
11.若关于的方程有增根,则等于 .
12.已知,则 .
13.一个正数的平方根分别是和,则这个正数为 .
14.如图,,则的度数为 .
15.将正三角形、正四边形、正五边形按如图所示的位置摆放.如果,那么
.
16.把无理数,,,表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是 .
三.解答题(共8小题,满分52分,其中17题4分,18题8分,19、20每小题6分,21、22每小题7分,23题8分,24题6分)
17.计算: ;
18.解方程和不等式.
(1);
(2).
19.先化简:; 再在不等式组的整数解中选取一个合适的解作为的取值,代入求值.
20.先化简,再求值:,其中.
如图是小亮和小芳的解答过程.
(1) 的解法是错误的;
错误的原因在于未能正确地运用二次根式的性质: ;
(2)先化简,再求值:,其中.
21.倡导健康生活推进全民健身,某社区去年购进,两种健身器材若干件,经了解,种健身器材的单价是种健身器材的1.5倍,用7200元购买种健身器材比用5400元购买种健身器材多10件.
(1),两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进,两种健身器材共50件,且费用不超过21000元,请问:种健身器材至少要购买多少件?
22.如图,和是等腰直角三角形.
(1)探究和的数量关系并证明;
(2)延长和交于点,利用图2补全图形,求的度数.
23.某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克元,售价每千克16元;乙种蔬菜进价每千克元,售价每千克18元.
(1)该超市购进甲种蔬菜10千克和乙种蔬菜5千克需要170元;购进甲种蔬菜6千克和乙种蔬菜10千克需要200元.求,的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜千克为整数),求有哪几种购买方案.
(3)在(2)的条件下,求超市在获得的利润的最大值.
24.小聪与同桌小明在课下学习中遇到这样一道数学题:“如图(1),在等边三角形中,点在上,点在的延长线上,且,试确定线段与的大小关系,并说明理由”.小敏与小颖讨论后,进行了如下解答:
(1)取特殊情况,探索讨论:
当点为的中点时,如图(2),确定线段与的大小关系,请你写出结论:
(填“”,“ ”或“” ,并说明理由.
(2)特例启发,解答题目:
解:题目中,与的大小关系是: (填“”,“ ”或“” .理由如下:如图(3),过点作,交于点.(请你将剩余的解答过程完成)
(3)拓展结论,设计新题:
在等边三角形中,点在直线上,点在直线上,且,若的边长为1,,则的长为 .(请你画出图形,并直接写出结果).
湖南省澧县张公庙中学2020年(秋季)八年级数学上册期末复习试卷(二)参考简答
一.选择题(共8小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
二.填空题(共8小题)
9. . 10. 4 . 11. . 12. . 13. 4 .
14. . 15. 72 . 16. .
三.解答题(共8小题)
17.计算:
(1);
(2).
【解】:(1)原式
;
(2)原式
.
18.解方程和不等式.
(1);
(2).
【解】:(1)不等式整理得:,
移项合并得:,
解得:;
(2)去分母得:,
解得:,
经检验是分式方程的解.
19.先化简:; 再在不等式组的整数解中选取一个合适的解作为的取值,代入求值.
【解】:原式
,
解不等式,得:,
解不等式,得:,
则不等式组的解集为,
其整数解有、0、1,
,
, 则原式.
20.先化简,再求值:,其中.
如图是小亮和小芳的解答过程.
(1) 的解法是错误的;
错误的原因在于未能正确地运用二次根式的性质: ;
(2)先化简,再求值:,其中.
【解】:(1)小亮的解法是错误的,
错误的原因在于未能正确地运用二次根式的性质:,
(2)原式,
,
原式.
21.倡导健康生活推进全民健身,某社区去年购进,两种健身器材若干件,经了解,种健身器材的单价是种健身器材的1.5倍,用7200元购买种健身器材比用5400元购买种健身器材多10件.
(1),两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进,两种健身器材共50件,且费用不超过21000元,请问:种健身器材至少要购买多少件?
【解】:(1)设种型号健身器材的单价为元套,种型号健身器材的单价为元套,
根据题意,可得:,
解得:,
经检验是原方程的根,
(元,
因此,,两种健身器材的单价分别是360元,540元;
(2)设购买种型号健身器材套,则购买种型号的健身器材套,
根据题意,可得:,
解得:,
因此,种型号健身器材至少购买34套.
22.如图,和是等腰直角三角形.
(1)探究和的数量关系并证明;
(2)延长和交于点,利用图2补全图形,求的度数.
【解】:(1),
理由如下:
和是等腰直角三角形,
,,,
,
即,
在和中,
, ,
;
(2)如图,即为补全的图形,
由(1)知,
,
是等腰直角三角形,
,
,
,
.
23.某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克元,售价每千克16元;乙种蔬菜进价每千克元,售价每千克18元.
(1)该超市购进甲种蔬菜10千克和乙种蔬菜5千克需要170元;购进甲种蔬菜6千克和乙种蔬菜10千克需要200元.求,的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜千克为整数),求有哪几种购买方案.
(3)在(2)的条件下,求超市在获得的利润的最大值.
【解】:(1)依题意,得:
, 解得:.
答:的值为10,的值为14.
(2)设购买甲种蔬菜千克,则购买乙种蔬菜千克,
依题意,得:, 解得:.
为正整数,
,59,60,
有3种购买方案,方案1:购买甲种蔬菜58千克,乙种蔬菜42千克;方案2:购买甲种蔬菜59千克,乙种蔬菜41千克;方案3:购买甲种蔬菜60千克,乙种蔬菜40千克.
(3)设超市获得的利润为元,则.
当时,取得最大值,最大值为.
24.小聪与同桌小明在课下学习中遇到这样一道数学题:“如图(1),在等边三角形中,点在上,点在的延长线上,且,试确定线段与的大小关系,并说明理由”.小敏与小颖讨论后,进行了如下解答:
(1)取特殊情况,探索讨论:
当点为的中点时,如图(2),确定线段与的大小关系,请你写出结论:
(填“”,“ ”或“” ,并说明理由.
(2)特例启发,解答题目:
解:题目中,与的大小关系是: (填“”,“ ”或“” .理由如下:如图(3),过点作,交于点.(请你将剩余的解答过程完成)
(3)拓展结论,设计新题:
在等边三角形中,点在直线上,点在直线上,且,若的边长为1,,则的长为 .(请你画出图形,并直接写出结果).
【解】:(1),
理由如下:,
,
三角形是等边三角形,
,
点为的中点,
,
,
,
,
,
,
(2)如图3,
为等边三角形,且,
,,,
,
,
,,
在与中,
, ,
,
, 为等边三角形,
,,
(3)如图4,
当点在的延长线上时,过点作,交的延长线于点,
则,,,,
为等边三角形,
,
,,
,而,
,,
在与中,
, ,
,
为等边三角形,
,,
;
如图5,
当点在的延长线上时,过点作,交的延长线于点,
类似上述解法,同理可证:,,
,
综上可得为:3或1.
同课章节目录
