西师大版数学六年级下册 2.2圆柱的体积 教案
文档属性
| 名称 | 西师大版数学六年级下册 2.2圆柱的体积 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 08:19:08 | ||
图片预览


文档简介
第2课时 圆柱的体积
【教学目标】
1.知道圆柱体积计算公式的推导过程,会应用该公式计算圆柱的体积。
2.通过动手操作与课件演示,让学生经历推导圆柱体积公式的过程,并能熟记公式。
3.借助课件演示,培养学生抽象概括的思维能力,初步建立空间观念和逻辑推理能力。
【教学重点】
圆柱体积公式的推导和应用。
【教学难点】
理解圆柱体积公式的推导过程。
【教学过程】
一、新课引入
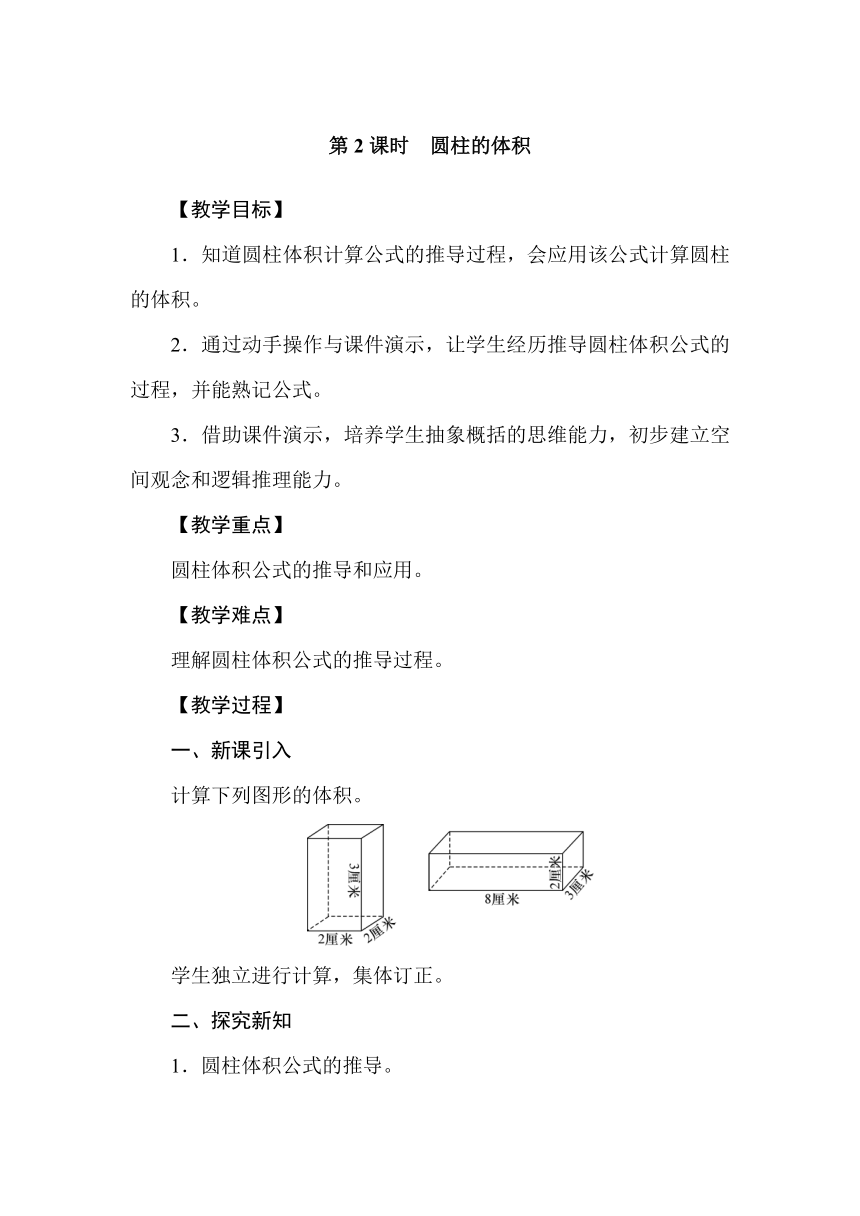
计算下列图形的体积。
学生独立进行计算,集体订正。
二、探究新知
1.圆柱体积公式的推导。
师:长方体、正方体的体积计算我们都已经知道了,那么圆柱的体积怎样计算呢?
下面我们一起看大屏幕。
把圆柱的底面分成许多相等的扇形(如分成16个),然后把圆柱切开,照下图拼起来,就近似于一个长方体。分成的扇形越多,拼成的立体图形就越接近于长方体。
长方形的体积=底面积×高
?
圆柱的体积=________
通过以上观察,你发现了什么?
学生总结后回答:
(1)平均分的份数越多,拼起来的图形越接近于长方体。
(2)平均分的份数越多,每份扇形的底面就越小,弧就越短。拼起来的长方体的长就越近似于一条线段,这样整个图形就越近似于长方体。
(3)拼成的近似的长方体和圆柱相比,底面的形状变了,由圆变成了近似的长方形,而底面的面积大小没有发生变化。
(4)近似长方体的高就是圆柱的高,没有变化。
由此得出:圆柱的体积V=Sh。
2.圆柱体积公式的应用。
师:如果求一个圆柱的体积,需要知道哪些条件呢?(底面积和高)请同学们看这道题,你会解决吗?
(出示教材第28页“试一试”)
圆柱的底面积是28.6cm2,高15cm,求圆柱的体积。
学生独立完成,指名板演,集体订正。
师:同学们完成得真好,如果一个圆柱不告诉我们底面积,告诉我们底面周长,那如何解决呢?请同学们在小组内交流一下吧。
学生汇报、交流。
生:可以先利用圆的周长公式求出底面半径,再求出圆柱的底面积,最后利用圆柱的体积公式V=Sh,求出这个圆柱的体积。
师:同学们回答得真好,请同学们独立完成下面这道题,你有没有信心?
(课件出示例4)
师:这个圆柱的体积是多少立方厘米?
学生独立完成,指名到黑板板演,交流、订正。
圆柱的底面半径:31.4÷3.14÷2=5(cm)
圆柱的底面积:3.14×52=78.5(cm2)
圆柱的体积:78.5×20=1570(cm3)
3.完成教材课堂活动。
(课件出示课堂活动)
学生讨论计算方法。计算容积时先测量出里面的直径和高,再计算,并交流计算过程和结果。
完成“议一议”。
容积与体积计算的相同点:都可以用底面积乘高这个公式来解决。
不同点:容积计算用从里面测量的数据,体积计算用从外面测量的数据。
三、巩固练习
1.学生独立完成下表,然后集体订正。
底面半径 高 表面积 体积
5cm 3cm
4cm 6cm
2.求下面圆柱的体积。(单位:cm)
学生独立完成后,小组内交流、订正。
教师板书第一个。
V=Sh=3.14×(4÷2)2×12=150.72(cm3)
3.教材练习八第3、5题。
学生独立完成,指名学生板演,全班交流。
四、课堂小结
谈谈本节课的收获与困惑。
【板书设计】
圆柱的体积
圆柱的体积公式:V=Sh
圆柱的底面半径:31.4÷3.14÷2=5(cm)
圆柱的底面积:3.14×52=78.5(cm2)
圆柱的体积:78.5×20=1570(cm3)
V=Sh=3.14×(4÷2)2×12=150.72(cm3)
【教学目标】
1.知道圆柱体积计算公式的推导过程,会应用该公式计算圆柱的体积。
2.通过动手操作与课件演示,让学生经历推导圆柱体积公式的过程,并能熟记公式。
3.借助课件演示,培养学生抽象概括的思维能力,初步建立空间观念和逻辑推理能力。
【教学重点】
圆柱体积公式的推导和应用。
【教学难点】
理解圆柱体积公式的推导过程。
【教学过程】
一、新课引入
计算下列图形的体积。
学生独立进行计算,集体订正。
二、探究新知
1.圆柱体积公式的推导。
师:长方体、正方体的体积计算我们都已经知道了,那么圆柱的体积怎样计算呢?
下面我们一起看大屏幕。
把圆柱的底面分成许多相等的扇形(如分成16个),然后把圆柱切开,照下图拼起来,就近似于一个长方体。分成的扇形越多,拼成的立体图形就越接近于长方体。
长方形的体积=底面积×高
?
圆柱的体积=________
通过以上观察,你发现了什么?
学生总结后回答:
(1)平均分的份数越多,拼起来的图形越接近于长方体。
(2)平均分的份数越多,每份扇形的底面就越小,弧就越短。拼起来的长方体的长就越近似于一条线段,这样整个图形就越近似于长方体。
(3)拼成的近似的长方体和圆柱相比,底面的形状变了,由圆变成了近似的长方形,而底面的面积大小没有发生变化。
(4)近似长方体的高就是圆柱的高,没有变化。
由此得出:圆柱的体积V=Sh。
2.圆柱体积公式的应用。
师:如果求一个圆柱的体积,需要知道哪些条件呢?(底面积和高)请同学们看这道题,你会解决吗?
(出示教材第28页“试一试”)
圆柱的底面积是28.6cm2,高15cm,求圆柱的体积。
学生独立完成,指名板演,集体订正。
师:同学们完成得真好,如果一个圆柱不告诉我们底面积,告诉我们底面周长,那如何解决呢?请同学们在小组内交流一下吧。
学生汇报、交流。
生:可以先利用圆的周长公式求出底面半径,再求出圆柱的底面积,最后利用圆柱的体积公式V=Sh,求出这个圆柱的体积。
师:同学们回答得真好,请同学们独立完成下面这道题,你有没有信心?
(课件出示例4)
师:这个圆柱的体积是多少立方厘米?
学生独立完成,指名到黑板板演,交流、订正。
圆柱的底面半径:31.4÷3.14÷2=5(cm)
圆柱的底面积:3.14×52=78.5(cm2)
圆柱的体积:78.5×20=1570(cm3)
3.完成教材课堂活动。
(课件出示课堂活动)
学生讨论计算方法。计算容积时先测量出里面的直径和高,再计算,并交流计算过程和结果。
完成“议一议”。
容积与体积计算的相同点:都可以用底面积乘高这个公式来解决。
不同点:容积计算用从里面测量的数据,体积计算用从外面测量的数据。
三、巩固练习
1.学生独立完成下表,然后集体订正。
底面半径 高 表面积 体积
5cm 3cm
4cm 6cm
2.求下面圆柱的体积。(单位:cm)
学生独立完成后,小组内交流、订正。
教师板书第一个。
V=Sh=3.14×(4÷2)2×12=150.72(cm3)
3.教材练习八第3、5题。
学生独立完成,指名学生板演,全班交流。
四、课堂小结
谈谈本节课的收获与困惑。
【板书设计】
圆柱的体积
圆柱的体积公式:V=Sh
圆柱的底面半径:31.4÷3.14÷2=5(cm)
圆柱的底面积:3.14×52=78.5(cm2)
圆柱的体积:78.5×20=1570(cm3)
V=Sh=3.14×(4÷2)2×12=150.72(cm3)
