江苏省连云港市智贤中学2020-2021学年高一12月月考数学试题 Word版含答案
文档属性
| 名称 | 江苏省连云港市智贤中学2020-2021学年高一12月月考数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 943.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 23:10:05 | ||
图片预览




文档简介
赣榆智贤中学2020-2021学年度第一学期高一年级月考
数学试题
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.( )
A. B. C. D.
2.函数的定义域为( )
A. B. C. D.
3.已知某扇形的弧长为,圆心角为,则该扇形的面积为( )
A. B. C. D.
4.若,则( )
A. B. C. D.
5.已知幂函数f(x)=xa的图象过点(3,),则函数g(x)=(2x-1)f(x)在区间[,2]上的最小值是( )
A.-1 B.0 C.-2 D.
6.某纯净水制造厂在净化过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少要过滤的次数为(取)( )
A.5 B.10 C.14 D.1
7.已知角的终边上有一点,则的值为( )
A.-2 B. C. D.
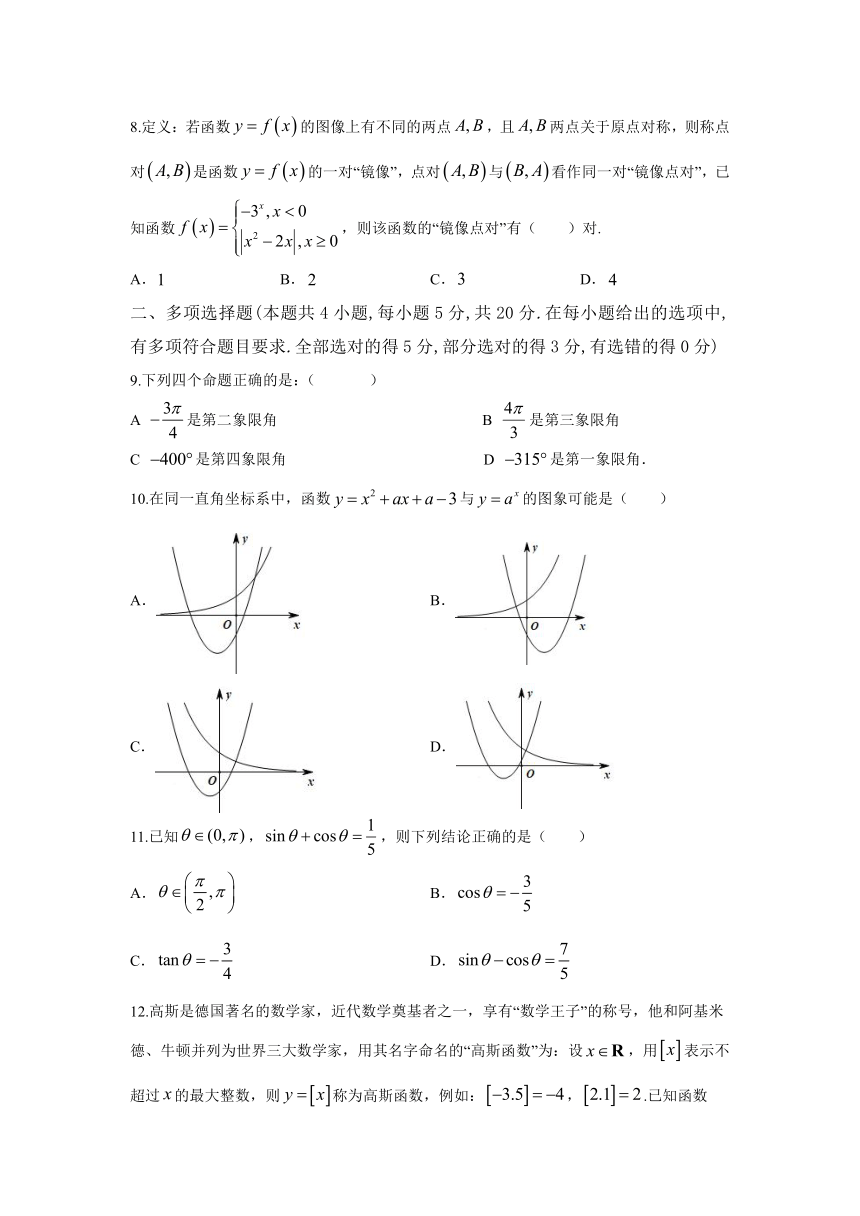
8.定义:若函数的图像上有不同的两点,且两点关于原点对称,则称点对是函数的一对“镜像”,点对与看作同一对“镜像点对”,已知函数,则该函数的“镜像点对”有( )对.
A. B. C. D.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.下列四个命题正确的是:( )
A 是第二象限角 B 是第三象限角
C 是第四象限角 D 是第一象限角.
10.在同一直角坐标系中,函数与的图象可能是( )
A. B.
C. D.
11.已知,,则下列结论正确的是( )
A. B.
C. D.
12.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设,用表示不超过的最大整数,则称为高斯函数,例如:,.已知函数,则关于函数的叙述中正确的是( )
A.是偶函数 B.是奇函数
C.在上是增函数 D.的值域是
三、填空题(本题共4小题,每小题5分,其中16题第一空2分,第二空3分,共20分)
13.已知角的终边过点,则的值是______.
14.若是定义在上的奇函数,当时,,则=_____;
15.已知,则的值为( )
16.设f(x)=,则的值为________.不等式的解集为_________.
四、解答题 (本题共6小题,第17题10分,其余各题12分,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(1)已知,且是第三象限角,求的值;
(2)已知,求的值.
18.已知函数(a>0,且a≠1)的图象经过点.
(1)求a的值;
(2)设不等式的解集为,求函数的值域.
19.已知,
(1)求的值; (2)求;
20.已知函数
(1)若,求方程的解;
(2)若对于,恒成立,求实数的取值范围.
21.已知函数,
(1)若,求实数的取值范围;
(2)当时,设函数的值域分别为,若,求实数的取值范围.
22.某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形挖去扇形后构成的).已知,线段、与弧、弧的长度之和为30米,圆心角为弧度.
(1)求关于的函数解析式;
(2)记铭牌的截面面积为,试问取何值时,的值最大?并求出最大值.
赣榆智贤中学2020-2021学年第一学期高一年级月考
数学试题
(时间:120分钟 满分:150分)
1.
【答案】C
2.
【答案】C
3.
【答案】D
扇形的圆心角,所以,则扇形的面积.
4.
【答案】A
5.
【答案】A
由题设,
故在上单调递增,
则当时取最小值,
6.
【答案】C
设过滤的次数为,原来水中杂质为,则,即,
所以,所以,所以,
因为,所以的最小值为,则至少要过滤次.
故选:C
7.
【答案】A
8.
【答案】C
由题意可知,函数的图像上有不同的两点,且两点关于原点对称,则称点对是函数的一对“镜像”,因为,由y轴左侧部分图像关于原点中心对称的图像,即,,作函数,和的图象如下:
由图像可知两图象有三个公共点,即该函数有3对“镜像点对”.
故选:C.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.
【答案】BCD
10.
【答案】AC
11.
【答案】ABD
①
,即,
,
,
,,
②
①加②得
①减②得
综上可得,正确的有ABD.
故选:ABD.
12.
【答案】BC
【详解】
,,
,则不是偶函数,故A错误;
的定义域为,
,
为奇函数,故B正确;
,
又在上单调递增,在上是增函数,故C正确;
,,则,可得,
即.
,故D错误.
三、填空题(本题共4小题,每小题5分,共20分)
13. 【答案】
14.【答案】
15.【答案】2
16.【答案】 或
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.
【答案】(1),;(2)见解析
(1)∵,∴.
又∵是第三象限角,
∴,即,
∴.
(2)∵,∴是第二或第三象限角.
当是第二象限角时,,,
∴,;
当是第三象限角时,,,
∴,.
18.
【详解】
(1)因为函数图象过点,所以a2-1=,解得a=.-----------5分
(2)f(x)=,
所以,解得,故,
因为x≥0,所以x-1≥-1,
所以0<=3.
所以函数的值域为(0,3].-----------7分
19.
【答案】【详解】(1)由已知,
化简得,整理得故------------6分
(2)
.------------6分
20.
【答案】(1)(2)
【详解】
(1),则,
由,整理为,
因为,
所以,可得.------------5分
(2)令,
由,
即,
恒成立,只需,
又在上为增函数,当时,,
所以.------------7分
21.
【答案】(1)(2)
【详解】
(1)即,所以,所以,所以,
所以实数的取值范围是.
(2)因为在上递增,所以当时,取得最小值,无最大值,所以,
设,因为,所以,所以,
因为在上递增,在上递减,
所以是,取得最大值,无最小值,所以,
因为,所以,得.
22.
【答案】(1);(2)当米时铭牌的面积最大,且最大面积为平方米.
【详解】
1)根据题意,可算得(), ().
又,
于是,,
所以,.
(2) 依据题意,可知
化简,得
.
于是,当(满足条件)时,().
答 所以当米时铭牌的面积最大,且最大面积为平方米.
【备用】
1
【答案】ABD
【详解】
因为,所以,A正确;
,B正确;
,C不正确;
,D正确.
(解答)
2.
【答案】(1)是;答案见解析;(2).
【详解】
解:(1)因为,
,即,
所以存在使得函数为“类函数”;
(2)由已知函数满足:,
则化简可得:①
令,则,
所以①可化为:在区间,上有解可使得函数为“类函数”,
即在,有解,
而函数在,上单调递增,所以当时,有最小值为,
所以,
故实数的取值范围为:,.
22.
【答案】(1);(2)存在,;(3)答案不唯一,见解析.
(1)∵定义域为,即恒成立
∴, 或得 综上得
(2)的定义域为,值域为∴ ,解得.
(3)令,则
若,则;
若,则;
若,则;
数学试题
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.( )
A. B. C. D.
2.函数的定义域为( )
A. B. C. D.
3.已知某扇形的弧长为,圆心角为,则该扇形的面积为( )
A. B. C. D.
4.若,则( )
A. B. C. D.
5.已知幂函数f(x)=xa的图象过点(3,),则函数g(x)=(2x-1)f(x)在区间[,2]上的最小值是( )
A.-1 B.0 C.-2 D.
6.某纯净水制造厂在净化过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少要过滤的次数为(取)( )
A.5 B.10 C.14 D.1
7.已知角的终边上有一点,则的值为( )
A.-2 B. C. D.
8.定义:若函数的图像上有不同的两点,且两点关于原点对称,则称点对是函数的一对“镜像”,点对与看作同一对“镜像点对”,已知函数,则该函数的“镜像点对”有( )对.
A. B. C. D.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.下列四个命题正确的是:( )
A 是第二象限角 B 是第三象限角
C 是第四象限角 D 是第一象限角.
10.在同一直角坐标系中,函数与的图象可能是( )
A. B.
C. D.
11.已知,,则下列结论正确的是( )
A. B.
C. D.
12.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设,用表示不超过的最大整数,则称为高斯函数,例如:,.已知函数,则关于函数的叙述中正确的是( )
A.是偶函数 B.是奇函数
C.在上是增函数 D.的值域是
三、填空题(本题共4小题,每小题5分,其中16题第一空2分,第二空3分,共20分)
13.已知角的终边过点,则的值是______.
14.若是定义在上的奇函数,当时,,则=_____;
15.已知,则的值为( )
16.设f(x)=,则的值为________.不等式的解集为_________.
四、解答题 (本题共6小题,第17题10分,其余各题12分,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(1)已知,且是第三象限角,求的值;
(2)已知,求的值.
18.已知函数(a>0,且a≠1)的图象经过点.
(1)求a的值;
(2)设不等式的解集为,求函数的值域.
19.已知,
(1)求的值; (2)求;
20.已知函数
(1)若,求方程的解;
(2)若对于,恒成立,求实数的取值范围.
21.已知函数,
(1)若,求实数的取值范围;
(2)当时,设函数的值域分别为,若,求实数的取值范围.
22.某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形挖去扇形后构成的).已知,线段、与弧、弧的长度之和为30米,圆心角为弧度.
(1)求关于的函数解析式;
(2)记铭牌的截面面积为,试问取何值时,的值最大?并求出最大值.
赣榆智贤中学2020-2021学年第一学期高一年级月考
数学试题
(时间:120分钟 满分:150分)
1.
【答案】C
2.
【答案】C
3.
【答案】D
扇形的圆心角,所以,则扇形的面积.
4.
【答案】A
5.
【答案】A
由题设,
故在上单调递增,
则当时取最小值,
6.
【答案】C
设过滤的次数为,原来水中杂质为,则,即,
所以,所以,所以,
因为,所以的最小值为,则至少要过滤次.
故选:C
7.
【答案】A
8.
【答案】C
由题意可知,函数的图像上有不同的两点,且两点关于原点对称,则称点对是函数的一对“镜像”,因为,由y轴左侧部分图像关于原点中心对称的图像,即,,作函数,和的图象如下:
由图像可知两图象有三个公共点,即该函数有3对“镜像点对”.
故选:C.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.
【答案】BCD
10.
【答案】AC
11.
【答案】ABD
①
,即,
,
,
,,
②
①加②得
①减②得
综上可得,正确的有ABD.
故选:ABD.
12.
【答案】BC
【详解】
,,
,则不是偶函数,故A错误;
的定义域为,
,
为奇函数,故B正确;
,
又在上单调递增,在上是增函数,故C正确;
,,则,可得,
即.
,故D错误.
三、填空题(本题共4小题,每小题5分,共20分)
13. 【答案】
14.【答案】
15.【答案】2
16.【答案】 或
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.
【答案】(1),;(2)见解析
(1)∵,∴.
又∵是第三象限角,
∴,即,
∴.
(2)∵,∴是第二或第三象限角.
当是第二象限角时,,,
∴,;
当是第三象限角时,,,
∴,.
18.
【详解】
(1)因为函数图象过点,所以a2-1=,解得a=.-----------5分
(2)f(x)=,
所以,解得,故,
因为x≥0,所以x-1≥-1,
所以0<=3.
所以函数的值域为(0,3].-----------7分
19.
【答案】【详解】(1)由已知,
化简得,整理得故------------6分
(2)
.------------6分
20.
【答案】(1)(2)
【详解】
(1),则,
由,整理为,
因为,
所以,可得.------------5分
(2)令,
由,
即,
恒成立,只需,
又在上为增函数,当时,,
所以.------------7分
21.
【答案】(1)(2)
【详解】
(1)即,所以,所以,所以,
所以实数的取值范围是.
(2)因为在上递增,所以当时,取得最小值,无最大值,所以,
设,因为,所以,所以,
因为在上递增,在上递减,
所以是,取得最大值,无最小值,所以,
因为,所以,得.
22.
【答案】(1);(2)当米时铭牌的面积最大,且最大面积为平方米.
【详解】
1)根据题意,可算得(), ().
又,
于是,,
所以,.
(2) 依据题意,可知
化简,得
.
于是,当(满足条件)时,().
答 所以当米时铭牌的面积最大,且最大面积为平方米.
【备用】
1
【答案】ABD
【详解】
因为,所以,A正确;
,B正确;
,C不正确;
,D正确.
(解答)
2.
【答案】(1)是;答案见解析;(2).
【详解】
解:(1)因为,
,即,
所以存在使得函数为“类函数”;
(2)由已知函数满足:,
则化简可得:①
令,则,
所以①可化为:在区间,上有解可使得函数为“类函数”,
即在,有解,
而函数在,上单调递增,所以当时,有最小值为,
所以,
故实数的取值范围为:,.
22.
【答案】(1);(2)存在,;(3)答案不唯一,见解析.
(1)∵定义域为,即恒成立
∴, 或得 综上得
(2)的定义域为,值域为∴ ,解得.
(3)令,则
若,则;
若,则;
若,则;
同课章节目录
