人教版数学 九年级上册24.4.1 弧长和扇形面积(1) 教学设计
文档属性
| 名称 | 人教版数学 九年级上册24.4.1 弧长和扇形面积(1) 教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 84.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 10:50:13 | ||
图片预览


文档简介
课程基本信息
课题
24.4.1弧长和扇形面积(1)
教科书
书名:
义务教育教科书
出版社:
人民教育出版社
出版日期:
2014
年
8月
教学目标
教学目标:(1)经历探索弧长和扇形面积公式的过程,培养学生的探索能力,并会利用弧长公式、扇形面积公式解决问题.
(2)在弧长和扇形面积计算公式的探究过程中,理解局部与整体之间的关系,感受转化、类比的数学思想.
教学重点:弧长公式及扇形面积公式的推导和应用
教学难点:利用扇形面积公式解决与弧有关的不规则图形的面积问题
教学过程
时间
教学环节
主要师生活动
1分钟
30秒
提出问题
教师通过复习与弧和弧长有关的概念,提出问题:弧长的大小由那些量来决定?如何求弧长呢?
学生通过观察和思考发现弧长与圆心角和半径有关,并思考弧长的求法
2分钟
问题探究一
师生循序渐进共同解决以下三个问题:
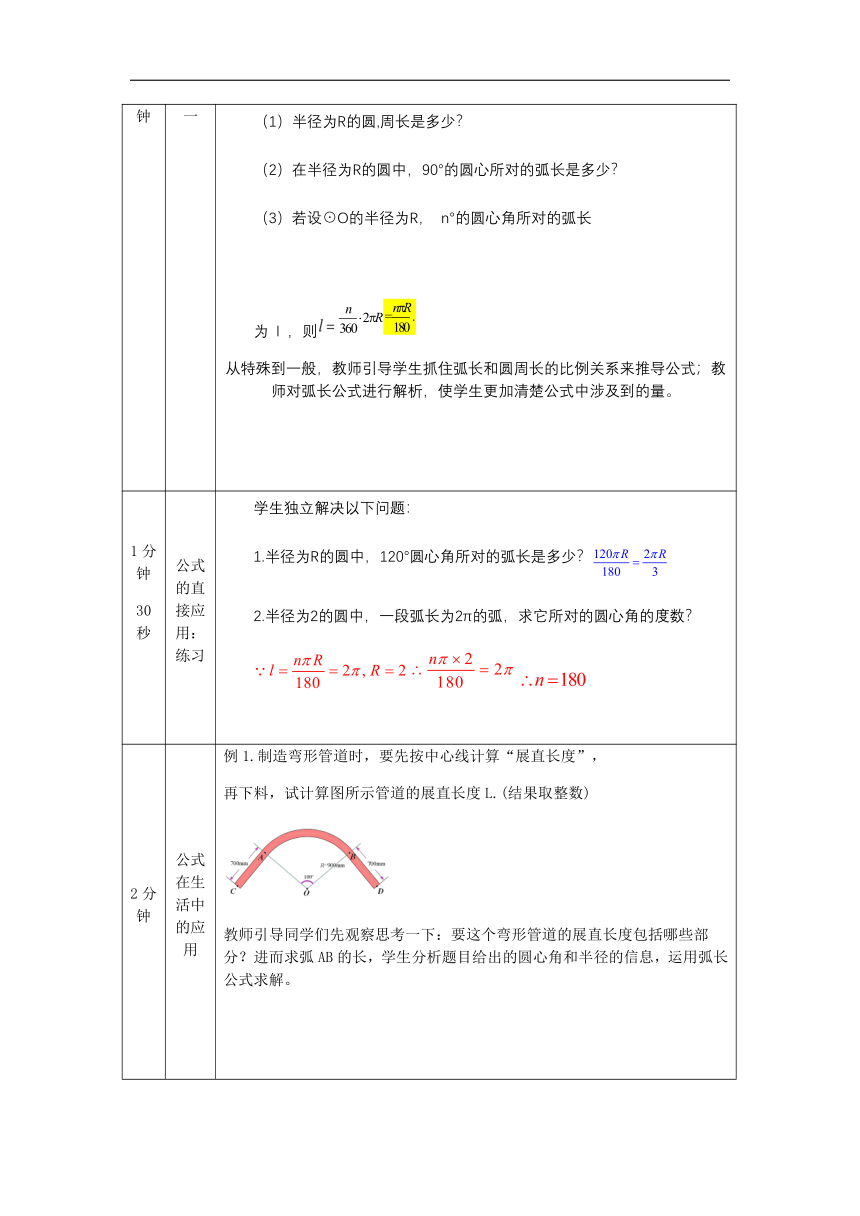
(1)半径为R的圆,周长是多少?
(2)在半径为R的圆中,90°的圆心所对的弧长是多少?
(3)若设⊙O的半径为R,
n°的圆心角所对的弧长
为
l
,则
从特殊到一般,教师引导学生抓住弧长和圆周长的比例关系来推导公式;教师对弧长公式进行解析,使学生更加清楚公式中涉及到的量。
1分钟
30秒
公式的直接应用:练习
学生独立解决以下问题:
1.半径为R的圆中,120°圆心角所对的弧长是多少?
2.半径为2的圆中,一段弧长为2π的弧,求它所对的圆心角的度数?
2分钟
公式在生活中的应用
例1.制造弯形管道时,要先按中心线计算“展直长度”,
再下料,试计算图所示管道的展直长度L.(结果取整数)
教师引导同学们先观察思考一下:要这个弯形管道的展直长度包括哪些部分?进而求弧AB的长,学生分析题目给出的圆心角和半径的信息,运用弧长公式求解。
2分钟
公式在几何图形圆中的应用
例2.
如图,在△AOC中,∠AOC=90°,∠C=20°,以O为
圆心,
OA为半径的圆交AC于点B,若OA=6,求弧AB的长。
2分钟
明确扇形的几何定义及表示方法
教师引导学生观察共同总结出扇形的几何定义;
1分钟
提出问题
教师提出问题:
(1)扇形的面积由哪些量决定?
(2)如何求扇形的面积呢?
学生通过前面弧长公式的学习,类比思考扇形面积的求法.
2分钟
问题探究二
学生尝试独立解决以下问题:
(1)半径为R的圆,面积是多少?
(2)若设⊙O的半径为R,圆心角为n°的扇形面积为
类比弧长公式的推导过程,得到扇形面积公式;教师对扇形面积公式进行解析,使学生更加清楚公式中涉及到的量。
2分钟
公式的直接应用:练习
学生独立解决以下问题:
1.
已知扇形的圆心角为120°,半径为2,则这个扇形的面积等于多少?
2.
已知扇形面积为1/3
π,圆心角为60°,则这个扇形的半径R等于多少?
3.
已知半径为2的扇形,其弧长为4/3
π,则这个扇形的圆心角为多少度?
教师加以指导
6分钟
公式在生活中的应用
例3.
如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m2)。
教师引导学生通过读题和识图,需要把文字语言和图形语言对应起来,
排水管道的截面就是图中的圆.把已知条件转化成几何元素标在图上,进而分析出所求面积=
S扇形OAB-
S△OAB
进而分别去求扇形和三角形的面积.
教师引导学生求扇形和三角形时需要的量,如何得到?最终解决问题。
1分钟
30秒
课堂小结
总结本节课所学的内容和方法,提升数学感悟能力。
(1)弧长公式和扇形面积公式分别是什么呢?
(2)你还记得我们是如何得到这两个公式的吗?如何运用呢?
10秒
布置作业
课后练习
1.已知扇形的圆心角为120°,半径为6,则扇形的弧长是(
).
A.3
B.4
C.5
D.6
2.如图所示,把边长为2的正方形ABCD的一边放在定直线L上,按顺时针方向绕点D旋转到如图的位置,则点B运动到点B′所经过的路线长度为_____.
3.
如图,在正方形ABCD中,分别以B,D为圆心,以正方形的边长a为画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为_________.
课题
24.4.1弧长和扇形面积(1)
教科书
书名:
义务教育教科书
出版社:
人民教育出版社
出版日期:
2014
年
8月
教学目标
教学目标:(1)经历探索弧长和扇形面积公式的过程,培养学生的探索能力,并会利用弧长公式、扇形面积公式解决问题.
(2)在弧长和扇形面积计算公式的探究过程中,理解局部与整体之间的关系,感受转化、类比的数学思想.
教学重点:弧长公式及扇形面积公式的推导和应用
教学难点:利用扇形面积公式解决与弧有关的不规则图形的面积问题
教学过程
时间
教学环节
主要师生活动
1分钟
30秒
提出问题
教师通过复习与弧和弧长有关的概念,提出问题:弧长的大小由那些量来决定?如何求弧长呢?
学生通过观察和思考发现弧长与圆心角和半径有关,并思考弧长的求法
2分钟
问题探究一
师生循序渐进共同解决以下三个问题:
(1)半径为R的圆,周长是多少?
(2)在半径为R的圆中,90°的圆心所对的弧长是多少?
(3)若设⊙O的半径为R,
n°的圆心角所对的弧长
为
l
,则
从特殊到一般,教师引导学生抓住弧长和圆周长的比例关系来推导公式;教师对弧长公式进行解析,使学生更加清楚公式中涉及到的量。
1分钟
30秒
公式的直接应用:练习
学生独立解决以下问题:
1.半径为R的圆中,120°圆心角所对的弧长是多少?
2.半径为2的圆中,一段弧长为2π的弧,求它所对的圆心角的度数?
2分钟
公式在生活中的应用
例1.制造弯形管道时,要先按中心线计算“展直长度”,
再下料,试计算图所示管道的展直长度L.(结果取整数)
教师引导同学们先观察思考一下:要这个弯形管道的展直长度包括哪些部分?进而求弧AB的长,学生分析题目给出的圆心角和半径的信息,运用弧长公式求解。
2分钟
公式在几何图形圆中的应用
例2.
如图,在△AOC中,∠AOC=90°,∠C=20°,以O为
圆心,
OA为半径的圆交AC于点B,若OA=6,求弧AB的长。
2分钟
明确扇形的几何定义及表示方法
教师引导学生观察共同总结出扇形的几何定义;
1分钟
提出问题
教师提出问题:
(1)扇形的面积由哪些量决定?
(2)如何求扇形的面积呢?
学生通过前面弧长公式的学习,类比思考扇形面积的求法.
2分钟
问题探究二
学生尝试独立解决以下问题:
(1)半径为R的圆,面积是多少?
(2)若设⊙O的半径为R,圆心角为n°的扇形面积为
类比弧长公式的推导过程,得到扇形面积公式;教师对扇形面积公式进行解析,使学生更加清楚公式中涉及到的量。
2分钟
公式的直接应用:练习
学生独立解决以下问题:
1.
已知扇形的圆心角为120°,半径为2,则这个扇形的面积等于多少?
2.
已知扇形面积为1/3
π,圆心角为60°,则这个扇形的半径R等于多少?
3.
已知半径为2的扇形,其弧长为4/3
π,则这个扇形的圆心角为多少度?
教师加以指导
6分钟
公式在生活中的应用
例3.
如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m2)。
教师引导学生通过读题和识图,需要把文字语言和图形语言对应起来,
排水管道的截面就是图中的圆.把已知条件转化成几何元素标在图上,进而分析出所求面积=
S扇形OAB-
S△OAB
进而分别去求扇形和三角形的面积.
教师引导学生求扇形和三角形时需要的量,如何得到?最终解决问题。
1分钟
30秒
课堂小结
总结本节课所学的内容和方法,提升数学感悟能力。
(1)弧长公式和扇形面积公式分别是什么呢?
(2)你还记得我们是如何得到这两个公式的吗?如何运用呢?
10秒
布置作业
课后练习
1.已知扇形的圆心角为120°,半径为6,则扇形的弧长是(
).
A.3
B.4
C.5
D.6
2.如图所示,把边长为2的正方形ABCD的一边放在定直线L上,按顺时针方向绕点D旋转到如图的位置,则点B运动到点B′所经过的路线长度为_____.
3.
如图,在正方形ABCD中,分别以B,D为圆心,以正方形的边长a为画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为_________.
同课章节目录
