人教版数学 九年级上册 圆全章复习 教学设计
文档属性
| 名称 | 人教版数学 九年级上册 圆全章复习 教学设计 | 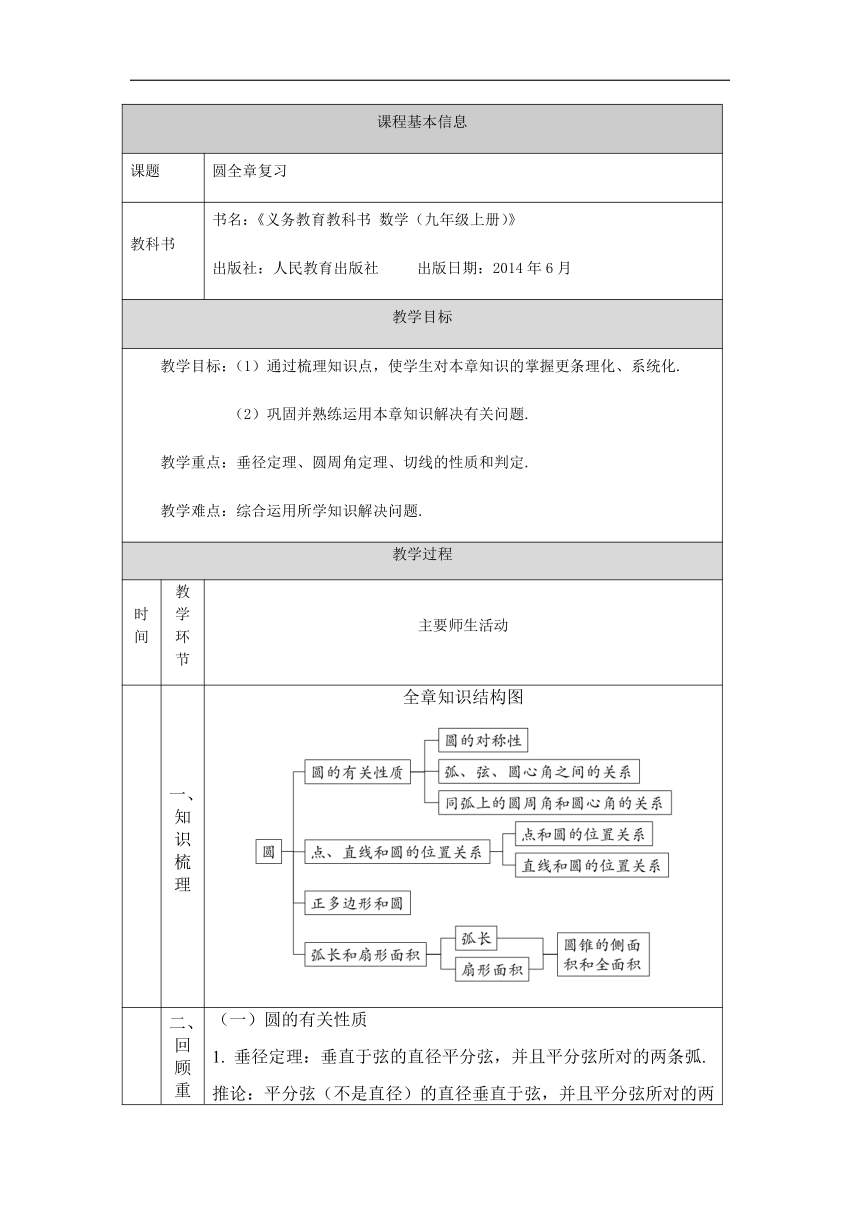 | |
| 格式 | zip | ||
| 文件大小 | 182.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 10:53:07 | ||
图片预览


文档简介
课程基本信息
课题
圆全章复习
教科书
书名:《义务教育教科书
数学(九年级上册)》
出版社:人民教育出版社
出版日期:2014年6月
教学目标
教学目标:(1)通过梳理知识点,使学生对本章知识的掌握更条理化、系统化.
(2)巩固并熟练运用本章知识解决有关问题.
教学重点:垂径定理、圆周角定理、切线的性质和判定.
教学难点:综合运用所学知识解决问题.
教学过程
时间
教学环节
主要师生活动
一、知识梳理
全章知识结构图
二、回顾重点,综合运用
(一)圆的有关性质
1.
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
∵直径CD垂直弦AB于M,
∴AM=BM,=,=.
∵直径CD平分弦AB,
∴CD⊥AB,=,=.
2.
弧、弦、圆心角之间的关系:在同圆或等圆中,两个圆心角、两条弧(优弧或劣弧)、两条弦中如果有一组量相等,则它们所对的其余各组量都相等.
3.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
∵∠A1,∠A2,∠A3所对的弧是,
∴∠A1=∠A2=∠A3=
∠BOC.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
推论3:圆内接四边形的对角互补.
【例1】如图,⊙O是△ABC的外接圆,若AB=6cm,∠C=60°,则⊙O的半径为________cm.
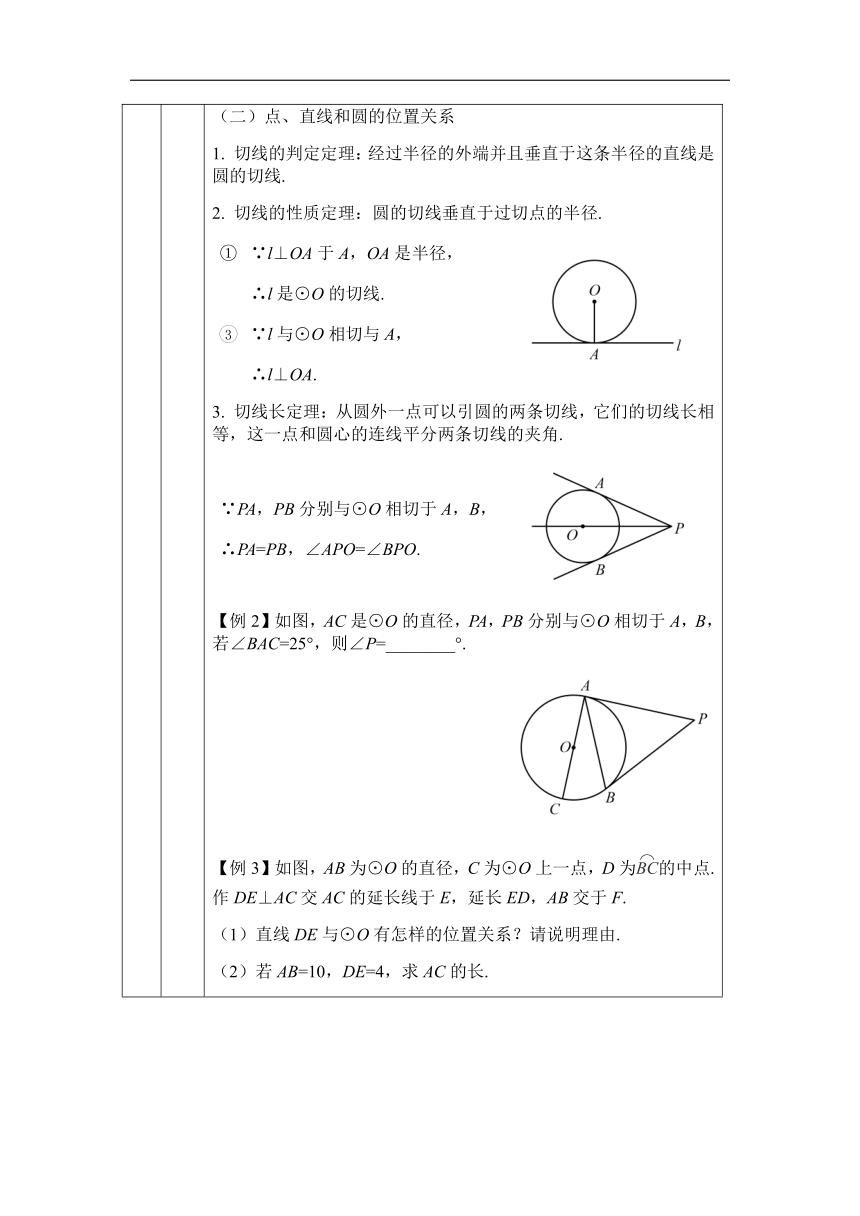
(二)点、直线和圆的位置关系
1.
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2.
切线的性质定理:圆的切线垂直于过切点的半径.
①
∵l⊥OA于A,OA是半径,
∴l是⊙O的切线.
∵l与⊙O相切与A,
∴l⊥OA.
3.
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
∵PA,PB分别与⊙O相切于A,B,
∴PA=PB,∠APO=∠BPO.
【例2】如图,AC是⊙O的直径,PA,PB分别与⊙O相切于A,B,若∠BAC=25°,则∠P=________°.
【例3】如图,AB为⊙O的直径,C为⊙O上一点,D为的中点.
作DE⊥AC交AC的延长线于E,延长ED,AB交于F.
(1)直线DE与⊙O有怎样的位置关系?请说明理由.
(2)若AB=10,DE=4,求AC的长.
(三)弧长和扇形面积
1.
弧长:在半径为R的圆中,n°的圆心角所对的弧长为.
2.
扇形面积:在半径为R的圆中,圆心角为n°的扇形面积为,其中l为扇形的弧长.
3.
圆锥的侧面积和全面积:若圆锥的母线长为l,底面半径为r,那么圆锥的侧面积为πrl,圆锥的全面积为πr(r+l).
【例4】如图,⊙O1的直径AB=2,若⊙O2经过A,B,且点O2在⊙O1上,则阴影部分的面积为___________.
三、课堂小结
【课堂小结】
梳理知识
归纳方法
综合运用
【布置作业】
如图,⊙O的直径CD=10
cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为(
).
(A)cm
(B)8
cm
(C)6
cm
(D)4
cm
一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角是(
).
(A)120°
(B)180°
(C)240°
(D)300°
如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C=_______°.
如图,点E是ABC的内心,AE的延长线和ABC的外接圆相交于点D.
求证:DE=DB.
课题
圆全章复习
教科书
书名:《义务教育教科书
数学(九年级上册)》
出版社:人民教育出版社
出版日期:2014年6月
教学目标
教学目标:(1)通过梳理知识点,使学生对本章知识的掌握更条理化、系统化.
(2)巩固并熟练运用本章知识解决有关问题.
教学重点:垂径定理、圆周角定理、切线的性质和判定.
教学难点:综合运用所学知识解决问题.
教学过程
时间
教学环节
主要师生活动
一、知识梳理
全章知识结构图
二、回顾重点,综合运用
(一)圆的有关性质
1.
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
∵直径CD垂直弦AB于M,
∴AM=BM,=,=.
∵直径CD平分弦AB,
∴CD⊥AB,=,=.
2.
弧、弦、圆心角之间的关系:在同圆或等圆中,两个圆心角、两条弧(优弧或劣弧)、两条弦中如果有一组量相等,则它们所对的其余各组量都相等.
3.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
∵∠A1,∠A2,∠A3所对的弧是,
∴∠A1=∠A2=∠A3=
∠BOC.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
推论3:圆内接四边形的对角互补.
【例1】如图,⊙O是△ABC的外接圆,若AB=6cm,∠C=60°,则⊙O的半径为________cm.
(二)点、直线和圆的位置关系
1.
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2.
切线的性质定理:圆的切线垂直于过切点的半径.
①
∵l⊥OA于A,OA是半径,
∴l是⊙O的切线.
∵l与⊙O相切与A,
∴l⊥OA.
3.
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
∵PA,PB分别与⊙O相切于A,B,
∴PA=PB,∠APO=∠BPO.
【例2】如图,AC是⊙O的直径,PA,PB分别与⊙O相切于A,B,若∠BAC=25°,则∠P=________°.
【例3】如图,AB为⊙O的直径,C为⊙O上一点,D为的中点.
作DE⊥AC交AC的延长线于E,延长ED,AB交于F.
(1)直线DE与⊙O有怎样的位置关系?请说明理由.
(2)若AB=10,DE=4,求AC的长.
(三)弧长和扇形面积
1.
弧长:在半径为R的圆中,n°的圆心角所对的弧长为.
2.
扇形面积:在半径为R的圆中,圆心角为n°的扇形面积为,其中l为扇形的弧长.
3.
圆锥的侧面积和全面积:若圆锥的母线长为l,底面半径为r,那么圆锥的侧面积为πrl,圆锥的全面积为πr(r+l).
【例4】如图,⊙O1的直径AB=2,若⊙O2经过A,B,且点O2在⊙O1上,则阴影部分的面积为___________.
三、课堂小结
【课堂小结】
梳理知识
归纳方法
综合运用
【布置作业】
如图,⊙O的直径CD=10
cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为(
).
(A)cm
(B)8
cm
(C)6
cm
(D)4
cm
一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角是(
).
(A)120°
(B)180°
(C)240°
(D)300°
如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C=_______°.
如图,点E是ABC的内心,AE的延长线和ABC的外接圆相交于点D.
求证:DE=DB.
同课章节目录
