24.1.2垂直于弦的直径(3)-1教学设计
文档属性
| 名称 | 24.1.2垂直于弦的直径(3)-1教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 08:26:03 | ||
图片预览


文档简介
课程基本信息
课题
24.1.2
垂直于弦的直径(3)
教科书
书名:
《义务教育教科书?数学(九年级上册)》
出版社:
人民教育出版社
出版日期:
2014
年
6
月
教学目标
教学目标:1.
复习巩固垂径定理;
会用垂径定理解决简单的实际问题.
教学重点:运用垂径定理实际问题.
教学难点:将实际问题转化为数学问题.
教学过程
时间
教学环节
主要师生活动
1min
活动一:
复习回顾
【活动一】复习回顾
复习垂径定理
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
如图
∵
在⊙O中,直径CD⊥弦AB于E,
∴
,
,
【活动二】巩固练习
如图,
如图AB是⊙O的直径,弦CD⊥AB于E,
如果AB=20,CD=16,那么线段OE的长为
.(OE长为6)
小结:
思路:
(由)垂径定理—构造直角三角形—(结合)勾股定理—建立方程.
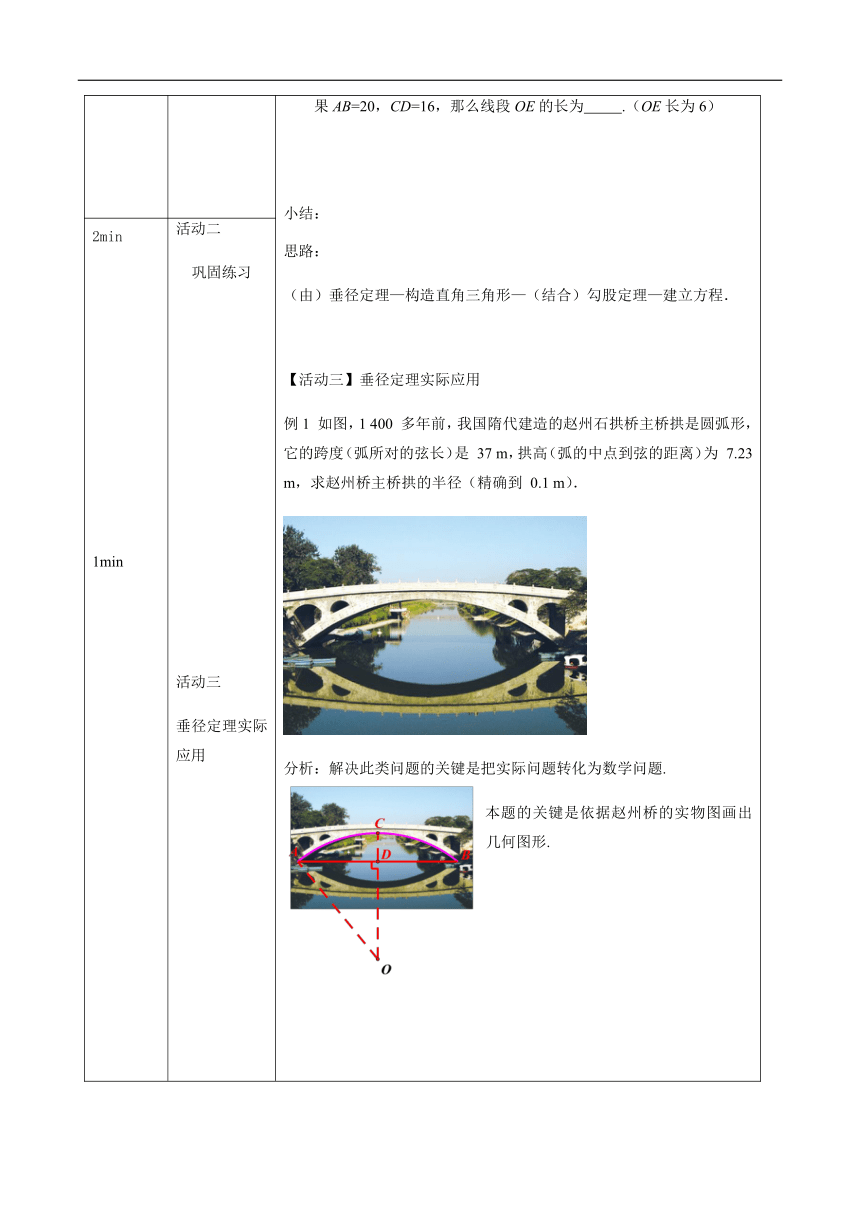
【活动三】垂径定理实际应用
例1
如图,1
400
多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是
37
m,拱高(弧的中点到弦的距离)为
7.23
m,求赵州桥主桥拱的半径(精确到
0.1
m).
分析:解决此类问题的关键是把实际问题转化为数学问题.
本题的关键是依据赵州桥的实物图画出几何图形.
解:如图,用表示主桥拱,设
所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,
D
为垂足,OC与相交于点C,
依据垂径定理,D是AB的中点,C是
的中点,CD就是拱高.
由题设可知
AB=37,CD=7.23,
∴OD=OC-CD=R-7.23.
在Rt△OAD中,由勾股定理,得
即
解得
R≈27.3
答:赵州桥主桥拱的半径约为27.3m.
小结:解决实际问题的主要步骤
1.
实际问题转化为数学问题
认真审题画出图形,并把题中的已知和未知用数学语言表示出来;
2.运用相关知识求得数学问题的解;
3.检验所求的数学问题的解是否符合实际意义;
4.回归到实际问题作答。
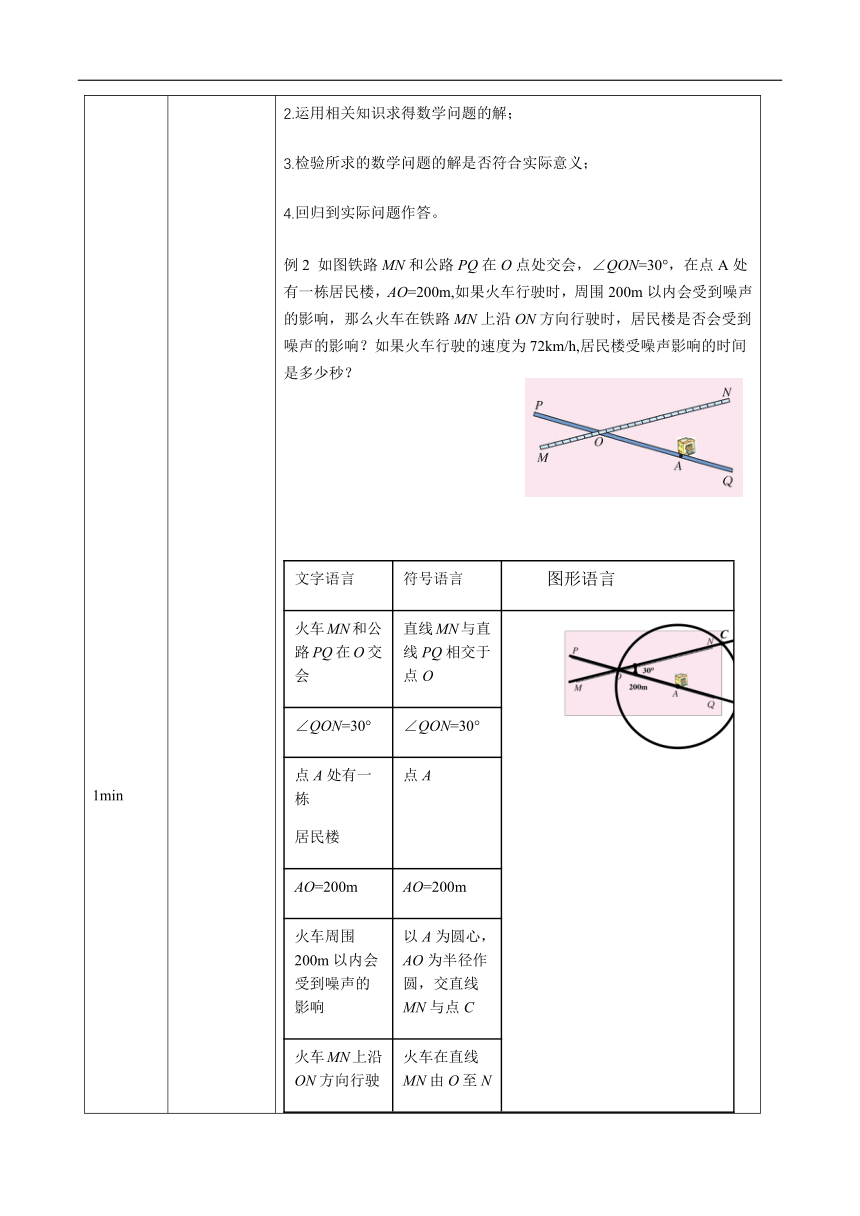
例2
如图铁路MN和公路PQ在O点处交会,∠QON=30°,在点A处有一栋居民楼,AO=200m,如果火车行驶时,周围200m以内会受到噪声的影响,那么火车在铁路MN上沿ON方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为72km/h,居民楼受噪声影响的时间是多少秒?
文字语言符号语言图形语言火车MN和公路PQ在O交会直线MN与直线PQ相交于点O∠QON=30°∠QON=30°点A处有一栋
居民楼点AAO=200mAO=200m火车周围200m以内会受到噪声的影响以A为圆心,AO为半径作圆,交直线MN与点C火车MN上沿ON方向行驶火车在直线MN由O至N运动速度为20m/s火车在弦OC的行驶时间(居民楼受影响的时间)
分析:
解:居民楼会受到火车噪声的影响.
以A为圆心AO为半径作圆,交直线MN于点C.
作AE⊥OC于E,
∴∠AEO=90°,.
∵在Rt△AEO中,∠QON=30°,AO=200,
∴
∵火车速度为20m/s,
∴居民楼受噪声影响的时间是
【活动四】课堂小结
运用垂径定理解决实际问题的一般步骤:
1.
把实际问题转化为数学问题.
依题意画出图形并把题中的已知和未知用把数学语言表示出来.
2.
根据相关知识求出数学问题的解.
思路:(由)垂径定理—构造直角三角形—(结合)勾股定理—建立方程.
3.
检验所求的数学问题的解是否符合实际意义.
4.
回归到实际问题作答.
【活动五】布置作业
同学们课后完成下面几道题
1.
如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆
的圆心,AB=300m,C是上一点,OC⊥AB,垂足为D,CD=45m,求这段弯路的半径.
2.
筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,2.5
m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为4m,求筒车工作时,盛水桶在水面以下的最大深度.
2min
1min
6min
1min
10min
1min
30s
活动二
巩固练习
活动三
垂径定理实际应用
【活动四】
课堂小结
【活动五】
布置作业
课题
24.1.2
垂直于弦的直径(3)
教科书
书名:
《义务教育教科书?数学(九年级上册)》
出版社:
人民教育出版社
出版日期:
2014
年
6
月
教学目标
教学目标:1.
复习巩固垂径定理;
会用垂径定理解决简单的实际问题.
教学重点:运用垂径定理实际问题.
教学难点:将实际问题转化为数学问题.
教学过程
时间
教学环节
主要师生活动
1min
活动一:
复习回顾
【活动一】复习回顾
复习垂径定理
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
如图
∵
在⊙O中,直径CD⊥弦AB于E,
∴
,
,
【活动二】巩固练习
如图,
如图AB是⊙O的直径,弦CD⊥AB于E,
如果AB=20,CD=16,那么线段OE的长为
.(OE长为6)
小结:
思路:
(由)垂径定理—构造直角三角形—(结合)勾股定理—建立方程.
【活动三】垂径定理实际应用
例1
如图,1
400
多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是
37
m,拱高(弧的中点到弦的距离)为
7.23
m,求赵州桥主桥拱的半径(精确到
0.1
m).
分析:解决此类问题的关键是把实际问题转化为数学问题.
本题的关键是依据赵州桥的实物图画出几何图形.
解:如图,用表示主桥拱,设
所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,
D
为垂足,OC与相交于点C,
依据垂径定理,D是AB的中点,C是
的中点,CD就是拱高.
由题设可知
AB=37,CD=7.23,
∴OD=OC-CD=R-7.23.
在Rt△OAD中,由勾股定理,得
即
解得
R≈27.3
答:赵州桥主桥拱的半径约为27.3m.
小结:解决实际问题的主要步骤
1.
实际问题转化为数学问题
认真审题画出图形,并把题中的已知和未知用数学语言表示出来;
2.运用相关知识求得数学问题的解;
3.检验所求的数学问题的解是否符合实际意义;
4.回归到实际问题作答。
例2
如图铁路MN和公路PQ在O点处交会,∠QON=30°,在点A处有一栋居民楼,AO=200m,如果火车行驶时,周围200m以内会受到噪声的影响,那么火车在铁路MN上沿ON方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为72km/h,居民楼受噪声影响的时间是多少秒?
文字语言符号语言图形语言火车MN和公路PQ在O交会直线MN与直线PQ相交于点O∠QON=30°∠QON=30°点A处有一栋
居民楼点AAO=200mAO=200m火车周围200m以内会受到噪声的影响以A为圆心,AO为半径作圆,交直线MN与点C火车MN上沿ON方向行驶火车在直线MN由O至N运动速度为20m/s火车在弦OC的行驶时间(居民楼受影响的时间)
分析:
解:居民楼会受到火车噪声的影响.
以A为圆心AO为半径作圆,交直线MN于点C.
作AE⊥OC于E,
∴∠AEO=90°,.
∵在Rt△AEO中,∠QON=30°,AO=200,
∴
∵火车速度为20m/s,
∴居民楼受噪声影响的时间是
【活动四】课堂小结
运用垂径定理解决实际问题的一般步骤:
1.
把实际问题转化为数学问题.
依题意画出图形并把题中的已知和未知用把数学语言表示出来.
2.
根据相关知识求出数学问题的解.
思路:(由)垂径定理—构造直角三角形—(结合)勾股定理—建立方程.
3.
检验所求的数学问题的解是否符合实际意义.
4.
回归到实际问题作答.
【活动五】布置作业
同学们课后完成下面几道题
1.
如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆
的圆心,AB=300m,C是上一点,OC⊥AB,垂足为D,CD=45m,求这段弯路的半径.
2.
筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,2.5
m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为4m,求筒车工作时,盛水桶在水面以下的最大深度.
2min
1min
6min
1min
10min
1min
30s
活动二
巩固练习
活动三
垂径定理实际应用
【活动四】
课堂小结
【活动五】
布置作业
同课章节目录
