18.1.1平行四边形的性质 课件(共28张PPT)
文档属性
| 名称 | 18.1.1平行四边形的性质 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 08:23:07 | ||
图片预览




文档简介
第十八章 四边形
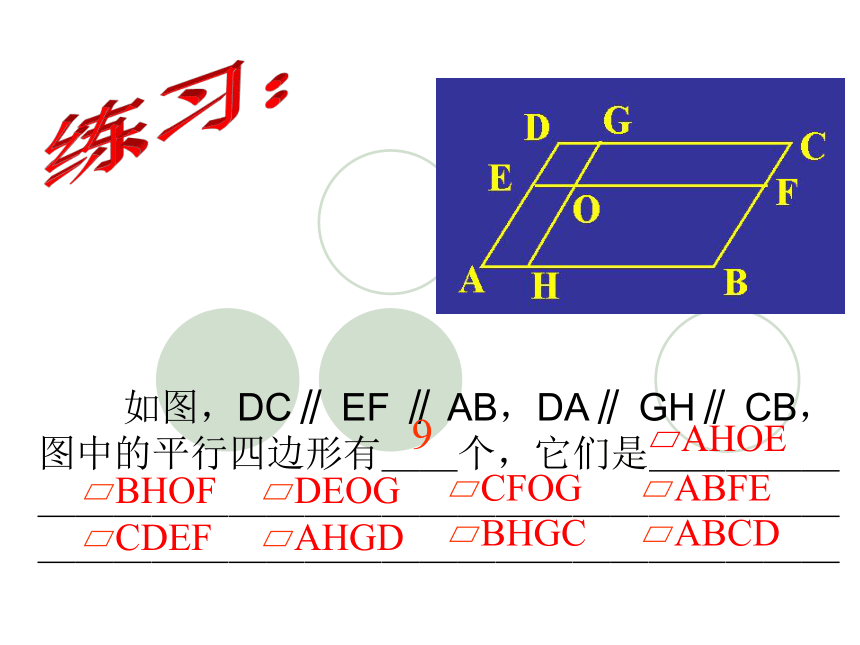
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
*
*
*
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
生活中处处有数学,需要我们有善于发现的眼睛.
下面的图片中,有你熟悉的哪些图形?
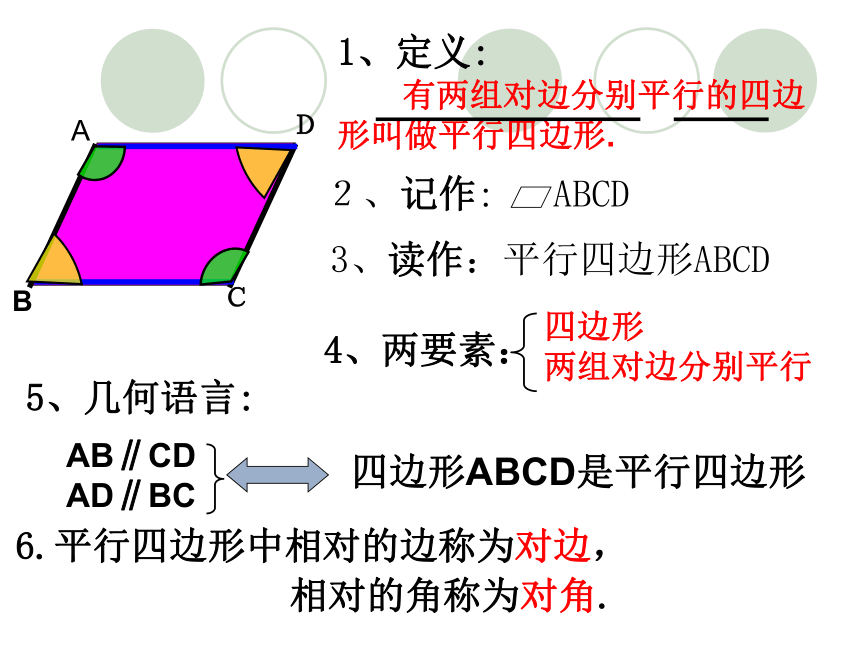
1、定义:
有两组对边分别平行的四边形叫做平行四边形.
2、记作: ABCD
5、几何语言:
4、两要素:
A
B
D
C
四边形ABCD是平行四边形
四边形
两组对边分别平行
AB∥CD
AD∥BC
3、读作:平行四边形ABCD
6.平行四边形中相对的边称为对边,
相对的角称为对角.
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
D
A
B
C
O
H
E
F
G
A
B
D
C
1、画一个平行四边形,观察它的边之间还有什么关系?
⑴平行四边形的对边平行.
∵四边形ABCD是平行四边形
∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形
∴AB=CD,BC=AD.
⑵平行四边形的对边相等.
探究平行四边形的性质:
●
●
C
A
B
D
平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D.
O
A
B
C
D
2.平行四边形的角具有哪些性质?
1、平行四边形的对边平行且相等.
平行四边形的性质
A
B
C
D
猜想:
2、平行四边形的对角相等.
用符号语言表示:
ABCD
AD∥ BC AB∥ DC
AD=BC AB=DC
∠ A=∠ C ∠ B=∠ D
已知:□ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
A
B
C
D
1
2
3
4
⌒
⌒
⌒
∵四边形ABCD是平行四边形
D
C
A
B
性质1: 平行四边形的对边相等.
性质2: 平行四边形的对角相等.
通过证明,知道 □ABCD
的结论:
边:AB=CD, AD=BC;
角:∠DAB=∠BCD,∠ABC=∠CDA
★平行四边形的性质是证明线段相等和角相等的重要依据和方法.
结论:平行四边形的邻角互补.
A
B
C
D
思考:平行四边形中相邻的两内角有什么关系呢?
分析:∵BC//AD, ∴∠A+∠B=180°,
同理,∠A+∠D=180° ,∠B+∠C=180°
∠D+∠C=180°
1、如图:在□ABCD 中,根据已知你能得到哪些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小试牛刀:
⌒
⌒
⌒
⌒
2、判断题(对的在括号内填“∨”,错的填“×”)
(1)平行四边形两组对边分别平行. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=35°,
那么∠B=55°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠B=145°. ( )
×
√
√
√
×
√
A
D
B
C
40
3.在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ;AB= ;
∠A= , ∠C= , ∠D=
30
120°
120°
60°
4.在 ABCD 中,∠ADC=120°, ∠CAD=20°,则∠ABC= , ∠CAB=
120°
40°
5.在平行四边形ABCD中,AB=4cm,BC=6cm,则这个平行四边形的周长为 .
20cm
B
C
D
A
⑶
⑷
⑸
6.如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解: ∵四边形ABCD是平行四边形,
∴ AB=CD,AD=BC
又 AB+BC+CD+AD=36m.
∵ AB=8m,
∴ CD=8m,
∴ AD=BC=10m.
3cm
A
B
D
C
5cm
4cm
7.求如图所示的 四边形ABCD的面积.
3cm
8.如图,在□ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
B
A
D
C
B
E
⑻
5
3
⌒
⌒
⌒
1
2
3
A
B
D
C
E
9cm
5cm
9.如图所示,四边形ABCD是平行四边形,若BE平分∠ABC,则DE= .
4cm
2
3
5cm
5cm
4cm
1
10、如图,已知 ABCD 中,AD=3,BD⊥AD, 且BD=4, 你能求出平行四边形的周长吗?
A
D
C
B
4
3
16
5
5
3
11、学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
通过本节课的学习,你有什么收获?
1.定义:两组对边分别平行的四边形叫做平行四边形.
⑴对边平行
⑵对边相等
⑶对角相等
⑷邻角互补
2.平行四边形的性质:
作业
P90 1.2.
1.平行四边形具有而一般四边形不具有的性质是( )
A.外角和等于360° B.不稳定性
C.对角相等 D.一组对边相等
2. 在 ABCD中,∠A=65°,则∠D=( )
A. 105° B. 115° C.125° D. 65°
3.平行四边形相邻两边之比为3:5,它的周长为48cm,则这个平行四边形较短边长为 .
当堂检测
C
B
9cm
D
C
B
A
58°
28
32
58°
28
32
122°
5 :在 ABCD中,已知∠A =32。,求其余三个角的度数。
A
B
C
D
∵四边形ABCD是平行四边形
解:
且 ∠A =32。 (已知)
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴ ∠A + ∠B =180。(两直线平行,
同旁内角互补)
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。
6 :已知在 ABCD中,AB=6cm,BC=4cm,求 ABCD 的周长。
A
B
C
D
连结AC,已知 ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴C ABCD=AB+CD+BC+AD=6+6+4+4=20(cm)
7.如图,在?ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BM
B
D
C
E
F
A
M
证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BA
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM
9.从平行四边形的一个锐角的顶点做两条高线,如果这两条高线的夹角是135°,求这个平行四边形的锐角的度数.
45°
8.平行四边形ABCD中,AB= cm,BE⊥CD于E,且BE= cm,求平行四边形ABCD的面积.
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
结论:平行四边形的邻角互补.
A
B
C
D
思考:平行四边形中相邻的两内角有什么关系呢?
分析:∵BC//AD
∴∠A+∠B=180°, ∠D+∠C=180°
同理 ∠A+∠D=180° ,∠B+∠C=180°
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
2、判断题(对的在括号内填“∨”,错的填“×”)
(1)平行四边形两组对边分别平行. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和 3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=35°,那么∠B=55°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,那么∠B=145°. ( )
×
√
√
√
×
√
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
2、判断题(对的在括号内填“∨”,错的填“×”)
(1)平行四边形两组对边分别平行. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和 3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=35°,那么∠B=55°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,那么∠B=145°. ( )
×
√
√
√
×
√
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
A
B
D
C
E
F
例1:在平行四边形ABCD中,DE⊥AB ,BF⊥CD,垂足分别为E、F.求证:AE=CF
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(应用性质1)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
结论:平行四边形的邻角互补.
A
B
C
D
思考:平行四边形中相邻的两内角有什么关系呢?
分析:∵BC//AD
∴∠A+∠B=180°, ∠D+∠C=180°
同理 ∠A+∠D=180° ,∠B+∠C=180°
A
B
D
C
E
F
例1:在平行四边形ABCD中,DE⊥AB ,BF⊥CD,垂足分别为E、F.求证:AE=CF
DE=BF吗?
3cm
A
B
D
C
5cm
4cm
7.求如图所示的 ABCD的面积.
3cm
8.如图,在□ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
B
A
D
C
B
E
⑻
5
3
⌒
⌒
⌒
1
2
3
通过本节课的学习,你有什么收获?
1.定义:两组对边分别平行的四边形叫做平行四边形.
⑴对边平行
⑵对边相等
⑶对角相等
⑷邻角互补
2.平行四边形的性质:
1.平行四边形具有而一般四边形不具有的性质是( )
A.外角和等于360° B.不稳定性
C.对角相等 D.一组对边相等
2. 在 ABCD中,∠A=65°,则∠D=( )
A. 105° B. 115° C.125° D. 65°
3.平行四边形相邻两边之比为3:5,它的周长为48cm,则这个平行四边形较短边长为 .
当堂检测
C
B
9cm
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
7.如图,在?ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BM
B
D
C
E
F
A
M
证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BA
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
1.平行四边形具有而一般四边形不具有的性质是( )
A.外角和等于360° B.不稳定性
C.对角相等 D.一组对边相等
2. 在□ABCD中,∠A=65°,则∠D=( )
A. 105° B. 115° C.125° D. 65°
3.平行四边形相邻两边之比为3:5,它的周长为48cm,则这个平行四边形较短边长为 .
当堂检测
C
B
9cm
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
5 .在 □ABCD 中,已知∠A =32。,求其余三个角的度数.
A
B
C
D
∵四边形ABCD是平行四边形
解:
且 ∠A =32。 (已知)
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴ ∠A + ∠B =180。(两直线平行,
同旁内角互补)
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。
6.已知在□ABCD 中,AB=6cm,BC=4cm,求 □ABCD AB的周长.
A
B
C
D
连结AC,已知□ABCD 的周长等于20 cm,AC=7 cm,求△ABC的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴C ABCD=AB+CD+BC+AD=6+6+4+4=20(cm)
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
*
*
*
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
生活中处处有数学,需要我们有善于发现的眼睛.
下面的图片中,有你熟悉的哪些图形?
1、定义:
有两组对边分别平行的四边形叫做平行四边形.
2、记作: ABCD
5、几何语言:
4、两要素:
A
B
D
C
四边形ABCD是平行四边形
四边形
两组对边分别平行
AB∥CD
AD∥BC
3、读作:平行四边形ABCD
6.平行四边形中相对的边称为对边,
相对的角称为对角.
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
D
A
B
C
O
H
E
F
G
A
B
D
C
1、画一个平行四边形,观察它的边之间还有什么关系?
⑴平行四边形的对边平行.
∵四边形ABCD是平行四边形
∴AB ∥ CD,BC ∥ AD.
∵四边形ABCD是平行四边形
∴AB=CD,BC=AD.
⑵平行四边形的对边相等.
探究平行四边形的性质:
●
●
C
A
B
D
平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D.
O
A
B
C
D
2.平行四边形的角具有哪些性质?
1、平行四边形的对边平行且相等.
平行四边形的性质
A
B
C
D
猜想:
2、平行四边形的对角相等.
用符号语言表示:
ABCD
AD∥ BC AB∥ DC
AD=BC AB=DC
∠ A=∠ C ∠ B=∠ D
已知:□ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
A
B
C
D
1
2
3
4
⌒
⌒
⌒
∵四边形ABCD是平行四边形
D
C
A
B
性质1: 平行四边形的对边相等.
性质2: 平行四边形的对角相等.
通过证明,知道 □ABCD
的结论:
边:AB=CD, AD=BC;
角:∠DAB=∠BCD,∠ABC=∠CDA
★平行四边形的性质是证明线段相等和角相等的重要依据和方法.
结论:平行四边形的邻角互补.
A
B
C
D
思考:平行四边形中相邻的两内角有什么关系呢?
分析:∵BC//AD, ∴∠A+∠B=180°,
同理,∠A+∠D=180° ,∠B+∠C=180°
∠D+∠C=180°
1、如图:在□ABCD 中,根据已知你能得到哪些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小试牛刀:
⌒
⌒
⌒
⌒
2、判断题(对的在括号内填“∨”,错的填“×”)
(1)平行四边形两组对边分别平行. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=35°,
那么∠B=55°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠B=145°. ( )
×
√
√
√
×
√
A
D
B
C
40
3.在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ;AB= ;
∠A= , ∠C= , ∠D=
30
120°
120°
60°
4.在 ABCD 中,∠ADC=120°, ∠CAD=20°,则∠ABC= , ∠CAB=
120°
40°
5.在平行四边形ABCD中,AB=4cm,BC=6cm,则这个平行四边形的周长为 .
20cm
B
C
D
A
⑶
⑷
⑸
6.如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解: ∵四边形ABCD是平行四边形,
∴ AB=CD,AD=BC
又 AB+BC+CD+AD=36m.
∵ AB=8m,
∴ CD=8m,
∴ AD=BC=10m.
3cm
A
B
D
C
5cm
4cm
7.求如图所示的 四边形ABCD的面积.
3cm
8.如图,在□ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
B
A
D
C
B
E
⑻
5
3
⌒
⌒
⌒
1
2
3
A
B
D
C
E
9cm
5cm
9.如图所示,四边形ABCD是平行四边形,若BE平分∠ABC,则DE= .
4cm
2
3
5cm
5cm
4cm
1
10、如图,已知 ABCD 中,AD=3,BD⊥AD, 且BD=4, 你能求出平行四边形的周长吗?
A
D
C
B
4
3
16
5
5
3
11、学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
通过本节课的学习,你有什么收获?
1.定义:两组对边分别平行的四边形叫做平行四边形.
⑴对边平行
⑵对边相等
⑶对角相等
⑷邻角互补
2.平行四边形的性质:
作业
P90 1.2.
1.平行四边形具有而一般四边形不具有的性质是( )
A.外角和等于360° B.不稳定性
C.对角相等 D.一组对边相等
2. 在 ABCD中,∠A=65°,则∠D=( )
A. 105° B. 115° C.125° D. 65°
3.平行四边形相邻两边之比为3:5,它的周长为48cm,则这个平行四边形较短边长为 .
当堂检测
C
B
9cm
D
C
B
A
58°
28
32
58°
28
32
122°
5 :在 ABCD中,已知∠A =32。,求其余三个角的度数。
A
B
C
D
∵四边形ABCD是平行四边形
解:
且 ∠A =32。 (已知)
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴ ∠A + ∠B =180。(两直线平行,
同旁内角互补)
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。
6 :已知在 ABCD中,AB=6cm,BC=4cm,求 ABCD 的周长。
A
B
C
D
连结AC,已知 ABCD的周长等于20 cm,AC=7 cm,求△ABC的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴C ABCD=AB+CD+BC+AD=6+6+4+4=20(cm)
7.如图,在?ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BM
B
D
C
E
F
A
M
证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BA
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM
9.从平行四边形的一个锐角的顶点做两条高线,如果这两条高线的夹角是135°,求这个平行四边形的锐角的度数.
45°
8.平行四边形ABCD中,AB= cm,BE⊥CD于E,且BE= cm,求平行四边形ABCD的面积.
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
结论:平行四边形的邻角互补.
A
B
C
D
思考:平行四边形中相邻的两内角有什么关系呢?
分析:∵BC//AD
∴∠A+∠B=180°, ∠D+∠C=180°
同理 ∠A+∠D=180° ,∠B+∠C=180°
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
2、判断题(对的在括号内填“∨”,错的填“×”)
(1)平行四边形两组对边分别平行. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和 3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=35°,那么∠B=55°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,那么∠B=145°. ( )
×
√
√
√
×
√
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
2、判断题(对的在括号内填“∨”,错的填“×”)
(1)平行四边形两组对边分别平行. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和 3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=35°,那么∠B=55°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,那么∠B=145°. ( )
×
√
√
√
×
√
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
A
B
D
C
E
F
例1:在平行四边形ABCD中,DE⊥AB ,BF⊥CD,垂足分别为E、F.求证:AE=CF
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(应用性质1)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
结论:平行四边形的邻角互补.
A
B
C
D
思考:平行四边形中相邻的两内角有什么关系呢?
分析:∵BC//AD
∴∠A+∠B=180°, ∠D+∠C=180°
同理 ∠A+∠D=180° ,∠B+∠C=180°
A
B
D
C
E
F
例1:在平行四边形ABCD中,DE⊥AB ,BF⊥CD,垂足分别为E、F.求证:AE=CF
DE=BF吗?
3cm
A
B
D
C
5cm
4cm
7.求如图所示的 ABCD的面积.
3cm
8.如图,在□ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
B
A
D
C
B
E
⑻
5
3
⌒
⌒
⌒
1
2
3
通过本节课的学习,你有什么收获?
1.定义:两组对边分别平行的四边形叫做平行四边形.
⑴对边平行
⑵对边相等
⑶对角相等
⑷邻角互补
2.平行四边形的性质:
1.平行四边形具有而一般四边形不具有的性质是( )
A.外角和等于360° B.不稳定性
C.对角相等 D.一组对边相等
2. 在 ABCD中,∠A=65°,则∠D=( )
A. 105° B. 115° C.125° D. 65°
3.平行四边形相邻两边之比为3:5,它的周长为48cm,则这个平行四边形较短边长为 .
当堂检测
C
B
9cm
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
7.如图,在?ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BM
B
D
C
E
F
A
M
证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BA
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM
第十八章 四边形
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
1.平行四边形具有而一般四边形不具有的性质是( )
A.外角和等于360° B.不稳定性
C.对角相等 D.一组对边相等
2. 在□ABCD中,∠A=65°,则∠D=( )
A. 105° B. 115° C.125° D. 65°
3.平行四边形相邻两边之比为3:5,它的周长为48cm,则这个平行四边形较短边长为 .
当堂检测
C
B
9cm
4.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
5 .在 □ABCD 中,已知∠A =32。,求其余三个角的度数.
A
B
C
D
∵四边形ABCD是平行四边形
解:
且 ∠A =32。 (已知)
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴ ∠A + ∠B =180。(两直线平行,
同旁内角互补)
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。
6.已知在□ABCD 中,AB=6cm,BC=4cm,求 □ABCD AB的周长.
A
B
C
D
连结AC,已知□ABCD 的周长等于20 cm,AC=7 cm,求△ABC的周长。
A
B
C
D
解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm
∴C ABCD=AB+CD+BC+AD=6+6+4+4=20(cm)
