18.1.2平行四边形的判定课件(共16张PPT)
文档属性
| 名称 | 18.1.2平行四边形的判定课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 677.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 07:05:30 | ||
图片预览



文档简介
初中数学八年级下册
平行四边形的判定(二)
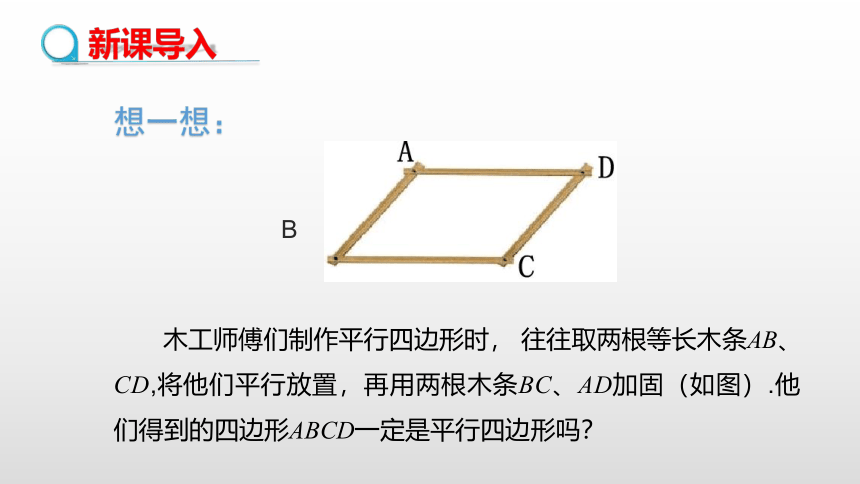
新课导入
想一想:
B
木工师傅们制作平行四边形时, 往往取两根等长木条AB、CD,将他们平行放置,再用两根木条BC、AD加固(如图).他们得到的四边形ABCD一定是平行四边形吗?
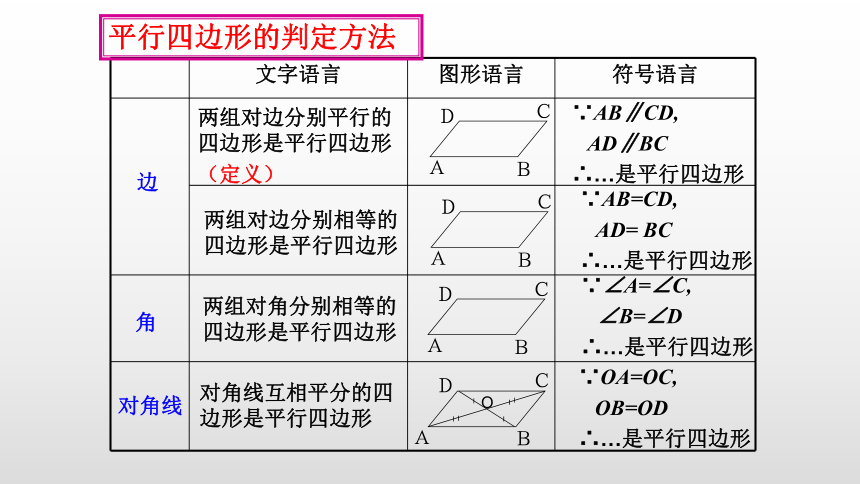
文字语言
图形语言
符号语言
A
B
C
D
A
B
C
D
O
A
B
C
D
A
B
C
D
两组对边分别平行的四边形是平行四边形
(定义)
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
∵OA=OC,
OB=OD
∴…是平行四边形
∵∠A=∠C,
∠B=∠D
∴…是平行四边形
∵AB=CD,
AD= BC
∴…是平行四边形
边
对角线
角
平行四边形的判定方法
B
D
A
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
∵AB=CD,AD= BC
∴四边形ABCD是平行四边形
∵AB∥CD, AB=CD
∴四边形ABCD是平行四边形
猜
想
洞察
学 习 目 标
掌握用一组对边平行且相等来判定平行四边形的方法.(重点)
会综合运用平行四边形的判定方法和性质来证明问题.(重点、难点)
1
2
知识讲解
A
B
C
D
1
2
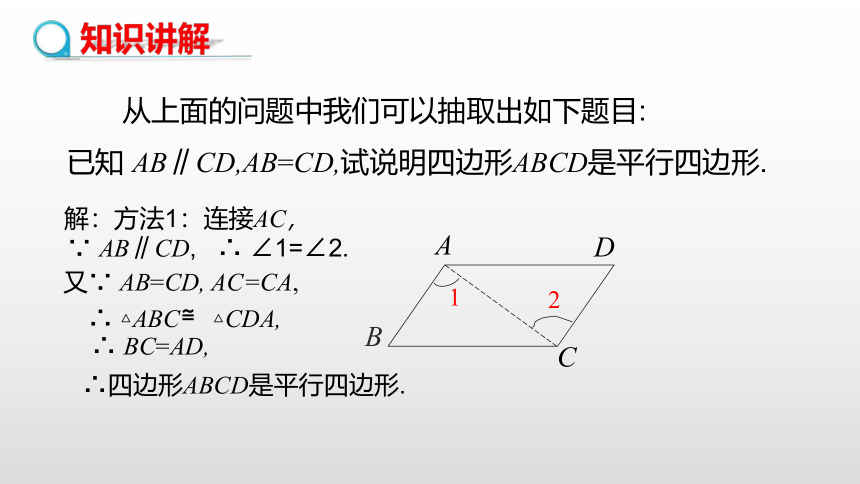
从上面的问题中我们可以抽取出如下题目:
已知 AB∥CD,AB=CD,试说明四边形ABCD是平行四边形.
解:方法1:连接AC,
∵ AB∥CD, ∴ ∠1=∠2.
又∵ AB=CD, AC=CA,
∴ △ABC≌△CDA,
∴ BC=AD,
∴四边形ABCD是平行四边形.
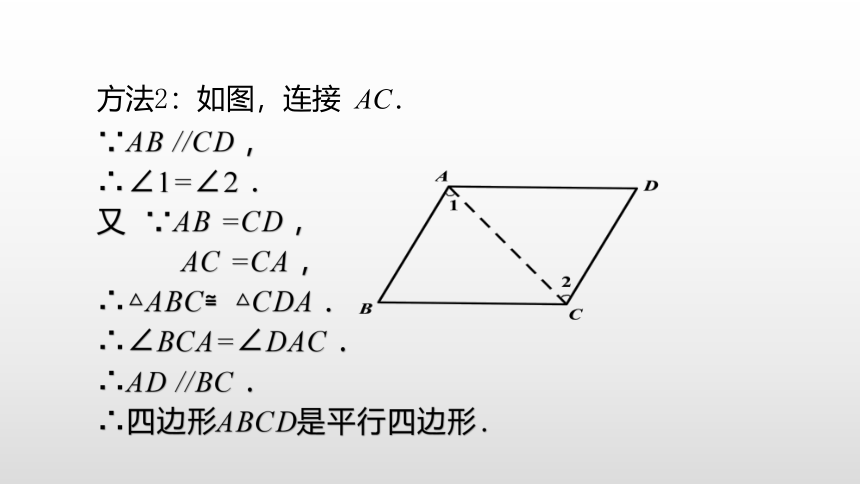
∵AB //CD ,
∴∠1=∠2 .
又 ∵AB =CD ,
AC =CA ,
∴△ABC≌△CDA .
∴∠BCA=∠DAC .
∴AD //BC .
∴四边形ABCD是平行四边形.
方法2:如图,连接 AC.
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB =CD, ∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
文字语言
图形语言
几何语言
判定
方法1
定义法
判定方法2
判定方法3
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形
两组对角分别相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
判定方法4
一组对边平行且相等的四边形是平行四边形
A
B
C
D
∵AB//CD, AB=CD,
∴四边形ABCD是
平行四边形
平行四边形的判定方法
证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
如果点E、F改为各是边AB、CD上的动点,且始终保持AE=CF时,以上结论是否还一定成立呢?
随堂训练
1.四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
提示:本题答案不唯一,如答案也可为AD∥BC.
3.如图,在 ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵ ∠AEF=∠CFE=90°,
∴ AE∥CF,
∴四边形AFCE是平行四边形.
已知:□ABCD中,对角线AC、BD相交于点
O,E、F、G、H分别为OA、OB、OC、OD的
中点.
求证:四边形EFGH是平行四边形.
拓展练习
请你用多种方法证明,并选出你认为最好的方法!
课堂小结
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
课堂小结
数学方法:
归纳、猜想、构图、方法最优化选择
数学思想::
转化
再见
平行四边形的判定(二)
新课导入
想一想:
B
木工师傅们制作平行四边形时, 往往取两根等长木条AB、CD,将他们平行放置,再用两根木条BC、AD加固(如图).他们得到的四边形ABCD一定是平行四边形吗?
文字语言
图形语言
符号语言
A
B
C
D
A
B
C
D
O
A
B
C
D
A
B
C
D
两组对边分别平行的四边形是平行四边形
(定义)
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
∵OA=OC,
OB=OD
∴…是平行四边形
∵∠A=∠C,
∠B=∠D
∴…是平行四边形
∵AB=CD,
AD= BC
∴…是平行四边形
边
对角线
角
平行四边形的判定方法
B
D
A
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
∵AB=CD,AD= BC
∴四边形ABCD是平行四边形
∵AB∥CD, AB=CD
∴四边形ABCD是平行四边形
猜
想
洞察
学 习 目 标
掌握用一组对边平行且相等来判定平行四边形的方法.(重点)
会综合运用平行四边形的判定方法和性质来证明问题.(重点、难点)
1
2
知识讲解
A
B
C
D
1
2
从上面的问题中我们可以抽取出如下题目:
已知 AB∥CD,AB=CD,试说明四边形ABCD是平行四边形.
解:方法1:连接AC,
∵ AB∥CD, ∴ ∠1=∠2.
又∵ AB=CD, AC=CA,
∴ △ABC≌△CDA,
∴ BC=AD,
∴四边形ABCD是平行四边形.
∵AB //CD ,
∴∠1=∠2 .
又 ∵AB =CD ,
AC =CA ,
∴△ABC≌△CDA .
∴∠BCA=∠DAC .
∴AD //BC .
∴四边形ABCD是平行四边形.
方法2:如图,连接 AC.
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB =CD, ∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
文字语言
图形语言
几何语言
判定
方法1
定义法
判定方法2
判定方法3
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形
两组对角分别相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
判定方法4
一组对边平行且相等的四边形是平行四边形
A
B
C
D
∵AB//CD, AB=CD,
∴四边形ABCD是
平行四边形
平行四边形的判定方法
证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
如果点E、F改为各是边AB、CD上的动点,且始终保持AE=CF时,以上结论是否还一定成立呢?
随堂训练
1.四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
提示:本题答案不唯一,如答案也可为AD∥BC.
3.如图,在 ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵ ∠AEF=∠CFE=90°,
∴ AE∥CF,
∴四边形AFCE是平行四边形.
已知:□ABCD中,对角线AC、BD相交于点
O,E、F、G、H分别为OA、OB、OC、OD的
中点.
求证:四边形EFGH是平行四边形.
拓展练习
请你用多种方法证明,并选出你认为最好的方法!
课堂小结
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
判定一个四边形是平行四边形的方法:
课堂小结
数学方法:
归纳、猜想、构图、方法最优化选择
数学思想::
转化
再见
