19.2.1正比例函数的图像(共18张PPT)
文档属性
| 名称 | 19.2.1正比例函数的图像(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:00:00 | ||
图片预览





文档简介
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
注意:
(1)常数与自变量的乘积
(2)自变量的指数为1
(3)自变量不能作为分母
判断下列函数是否是正比例函数,如果是请指出比例系数。
19.2.1正比例函数图像
第十九章 一次函数
作函数图象的一般步骤:
1、列表
2、描点
3、连线
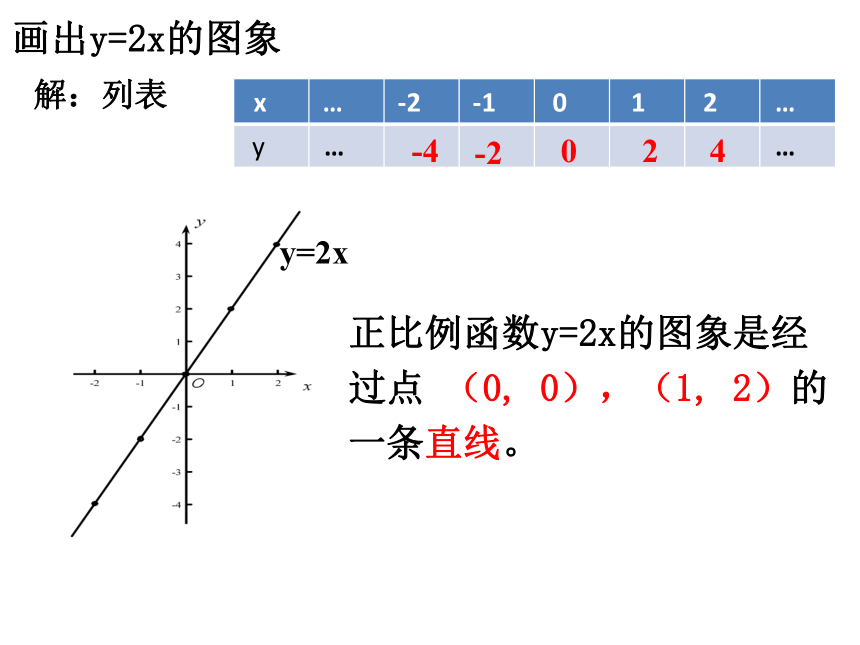
画出y=2x的图象
正比例函数y=2x的图象是经过点 (0, 0),(1, 2)的一条直线。
x
…
-2
-1
0
1
2
…
y
…
…
解:列表
-4
-2
0
2
4
y=2x
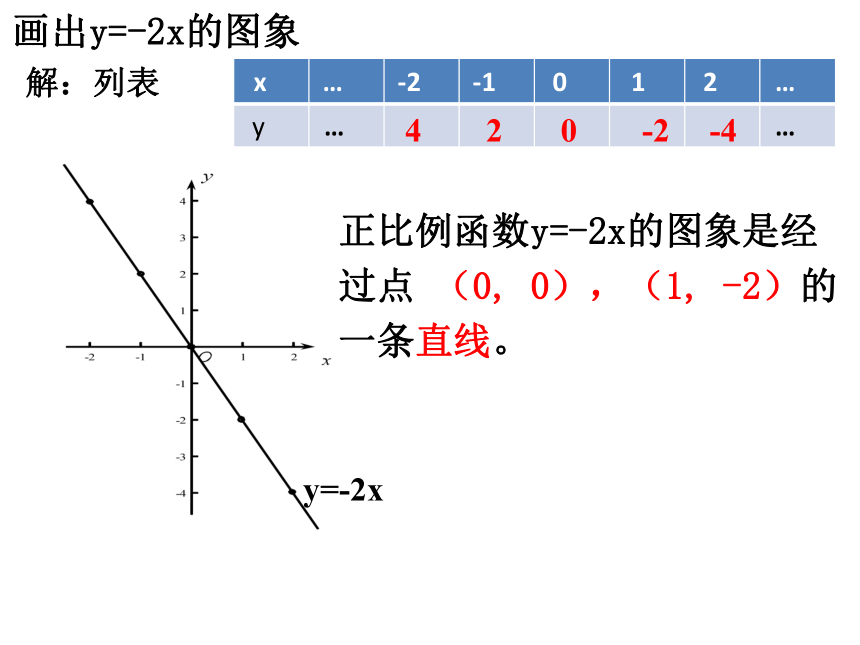
画出y=-2x的图象
正比例函数y=-2x的图象是经过点 (0, 0),(1, -2)的一条直线。
x
…
-2
-1
0
1
2
…
y
…
…
解:列表
4
2
0
-2
-4
y=-2x
一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx。
正比例函数的图象特征:
正比例函数图象的简单作法:
过(0,0)和(1,K )作直线
比较两个函数图象的相同点与不同点
函数y=2x的图象从左向右 ,经过第 象限,y随x的增大而 ;
函数y=-2x的图象从左向右 ,经过第 象限,y随x的增大而 。
上升
一、三
下降
二、四
k>0
k<0
增大
减小
两图象都是经过原点的直线
作出函数 和函数 的图像。
解:1、列表:
x
0
1
0
0
k>0
k<0
两图象都是经过原点的 ,
函数 的图象从左向右 ,经过第 象限,y随x的增大而 ;
函数 的图象从左向右 ,经过第 象限,y随x的增大而 。
直线
上升
一、三
下降
二、四
增大
减小
比较两个函数图象的相同点与不同点
在同一坐标系中作出函数y=x, y=3x, y=4x的图像(k>0)
解:列表
x
0
1
y=x
0
y=3x
0
y=4x
0
1
3
4
y=x
y=3x
y=4x
当k>0时,正比例函数图像经过一,三象限,图像从左向右上升,
随着x的增大y也增大。
在同一坐标系中作出函数y=-x, y=-3x, y=-4x的图像(k<0)
解:列表
x
0
1
y=-x
0
y=-3x
0
y=-4x
0
-1
-3
-4
y=-x
y=-3x
y=-4x
当k<0时,正比例函数图像经过二,四象限, 图像从左向右下降,
随着x的增大y反而减小。
作下列正比例函数的图象:
(1) ,
(2)y=3x , y=-3x
y=kx (k是常数,k≠0)的图象是一条经过原点的直线
y=kx
经过的象限
从左向右
Y随x的增大而
k>0
k<0
一,三
上升
增大
二,四
下降
减小
1、已知正比例函数的图像经过点(-2,-4);
(1)求这个正比例函数解析式;
(2)若这个函数的图形经过点A(a,2),求点A的坐标。
(3)如果自变量x的取值范围是0≤x≤5,求y的取值范围。
解:(1)设正比例函数解析式为y=kx
把点(-2,-4)代入得:
-4=-2k
解得:k=2
∴正比例函数解析式为y=2x
(2)把点A(a,2)代入y=2x得:
2=2a
解得a=1
∴点A(1.2)
(3)把x=0代入y=2x得:y=0
把x=5代入y=2x得:y=10
∴0≤y≤10
待定系数法
1、已知y与x+3成正比例,且当x=2时,y=-5;
(1)求这个函数解析式;
(2)若这个函数的图形经过点A(a,2),求点A的坐标。
已知y-1与x成正比例,且当x=2时,y=-5;
已知y-1与x+3成正比例,且当x=2时,y=-5;
1、已知甲、乙两人在一次赛跑中,路程s(m)与时间t(s)之间得关系如图所示,分别求出甲、乙两人得路程s与时间t的函数解析式,并写出自变量的取值范围。
A
B
O
s/m
100
12
12.5
t/s
1、已知正比例函数的图像经过点(-3,6);
(1)求这个正比例函数解析式;
(2)若这个函数的图形经过点A(a,2),求点A的坐标。
(3)如果自变量x的取值范围是0≤x≤5,求y的取值范围。
2、已知y与x-1成正比例,且当x=2时,y=-5;
(1)求这个函数解析式;
(2)若这个函数的图形经过点A(2,a),求点A的坐标。
注意:
(1)常数与自变量的乘积
(2)自变量的指数为1
(3)自变量不能作为分母
判断下列函数是否是正比例函数,如果是请指出比例系数。
19.2.1正比例函数图像
第十九章 一次函数
作函数图象的一般步骤:
1、列表
2、描点
3、连线
画出y=2x的图象
正比例函数y=2x的图象是经过点 (0, 0),(1, 2)的一条直线。
x
…
-2
-1
0
1
2
…
y
…
…
解:列表
-4
-2
0
2
4
y=2x
画出y=-2x的图象
正比例函数y=-2x的图象是经过点 (0, 0),(1, -2)的一条直线。
x
…
-2
-1
0
1
2
…
y
…
…
解:列表
4
2
0
-2
-4
y=-2x
一般地,正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx。
正比例函数的图象特征:
正比例函数图象的简单作法:
过(0,0)和(1,K )作直线
比较两个函数图象的相同点与不同点
函数y=2x的图象从左向右 ,经过第 象限,y随x的增大而 ;
函数y=-2x的图象从左向右 ,经过第 象限,y随x的增大而 。
上升
一、三
下降
二、四
k>0
k<0
增大
减小
两图象都是经过原点的直线
作出函数 和函数 的图像。
解:1、列表:
x
0
1
0
0
k>0
k<0
两图象都是经过原点的 ,
函数 的图象从左向右 ,经过第 象限,y随x的增大而 ;
函数 的图象从左向右 ,经过第 象限,y随x的增大而 。
直线
上升
一、三
下降
二、四
增大
减小
比较两个函数图象的相同点与不同点
在同一坐标系中作出函数y=x, y=3x, y=4x的图像(k>0)
解:列表
x
0
1
y=x
0
y=3x
0
y=4x
0
1
3
4
y=x
y=3x
y=4x
当k>0时,正比例函数图像经过一,三象限,图像从左向右上升,
随着x的增大y也增大。
在同一坐标系中作出函数y=-x, y=-3x, y=-4x的图像(k<0)
解:列表
x
0
1
y=-x
0
y=-3x
0
y=-4x
0
-1
-3
-4
y=-x
y=-3x
y=-4x
当k<0时,正比例函数图像经过二,四象限, 图像从左向右下降,
随着x的增大y反而减小。
作下列正比例函数的图象:
(1) ,
(2)y=3x , y=-3x
y=kx (k是常数,k≠0)的图象是一条经过原点的直线
y=kx
经过的象限
从左向右
Y随x的增大而
k>0
k<0
一,三
上升
增大
二,四
下降
减小
1、已知正比例函数的图像经过点(-2,-4);
(1)求这个正比例函数解析式;
(2)若这个函数的图形经过点A(a,2),求点A的坐标。
(3)如果自变量x的取值范围是0≤x≤5,求y的取值范围。
解:(1)设正比例函数解析式为y=kx
把点(-2,-4)代入得:
-4=-2k
解得:k=2
∴正比例函数解析式为y=2x
(2)把点A(a,2)代入y=2x得:
2=2a
解得a=1
∴点A(1.2)
(3)把x=0代入y=2x得:y=0
把x=5代入y=2x得:y=10
∴0≤y≤10
待定系数法
1、已知y与x+3成正比例,且当x=2时,y=-5;
(1)求这个函数解析式;
(2)若这个函数的图形经过点A(a,2),求点A的坐标。
已知y-1与x成正比例,且当x=2时,y=-5;
已知y-1与x+3成正比例,且当x=2时,y=-5;
1、已知甲、乙两人在一次赛跑中,路程s(m)与时间t(s)之间得关系如图所示,分别求出甲、乙两人得路程s与时间t的函数解析式,并写出自变量的取值范围。
A
B
O
s/m
100
12
12.5
t/s
1、已知正比例函数的图像经过点(-3,6);
(1)求这个正比例函数解析式;
(2)若这个函数的图形经过点A(a,2),求点A的坐标。
(3)如果自变量x的取值范围是0≤x≤5,求y的取值范围。
2、已知y与x-1成正比例,且当x=2时,y=-5;
(1)求这个函数解析式;
(2)若这个函数的图形经过点A(2,a),求点A的坐标。
