18.1.2 第2课时 平行四边形的判定(2) 课件 (共15张PPT)
文档属性
| 名称 | 18.1.2 第2课时 平行四边形的判定(2) 课件 (共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 385.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:00:00 | ||
图片预览





文档简介
导入新课
18.1.2 平行四边形判定
第2课时 平行四边形的判定(2)
第十八章 平行四边形
讲授新课
当堂练习
课堂小结
学习目标
掌握用一组对边平行且相等来判定平行四边形的方法.
学习重点:平行四边形各种判定方法及应用,根据不同条件能正
确地选择判定方法.
学习难点:平行四边形的判定定理与性质定理的综合应用.
复习引入
边
1.一组对边分别平行的四边形是平行四边形(定义)
2.两组对边分别相等的四边形是平行四边形
角
两组对角分别相等的四边形是平行四边形
对角线
两条对角线互相平分的四边形是平行四边形
回顾与思考
回忆平行四边形的判定定理:
平形四边形的判定
讲授新课
平行四边形的判定定理4
将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?链接AD、BC,四边形ABCD是什么样的图形?
A
D
C
B
猜测:一组对边平行且相等的四边形是平行四边形
证一证
已知:四边形ABCD中 AB∥CD, AB=CD
求证: 四边形ABCD是平行四边形.
判定定理4:
一组对边平行且相等的四边形是平行四边形.
A
D
C
B
证明:连接BD.
∵AB∥CD,∴C
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .
又AB= CD,
∴四边形ABCD是平行四边形.
1
2
知识要点
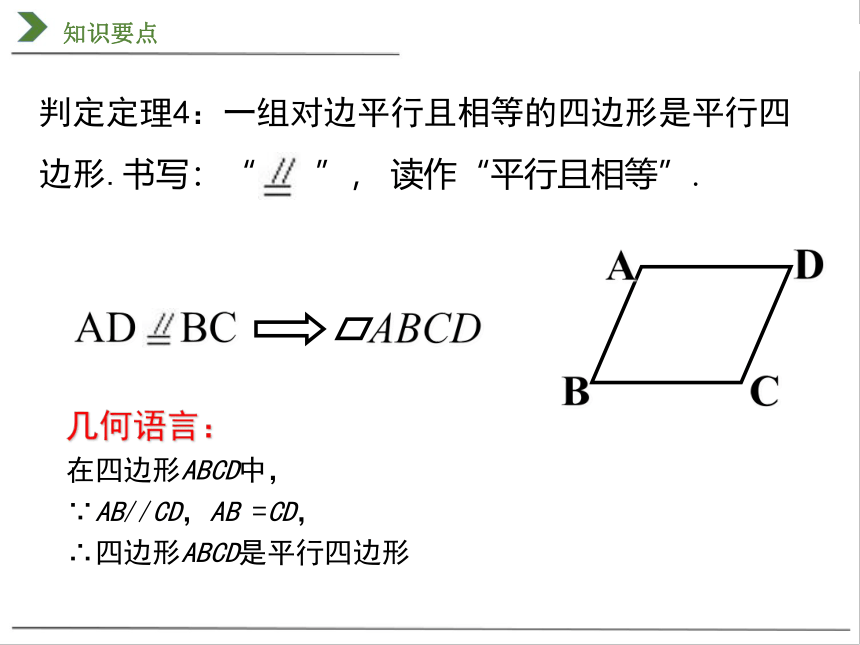
判定定理4:一组对边平行且相等的四边形是平行四边形.书写:“ ”, 读作“平行且相等”.
A
B
C
D
ABCD
AD BC
几何语言:
在四边形ABCD中,
∵AB//CD,AB =CD, ∴四边形ABCD是平行四边形
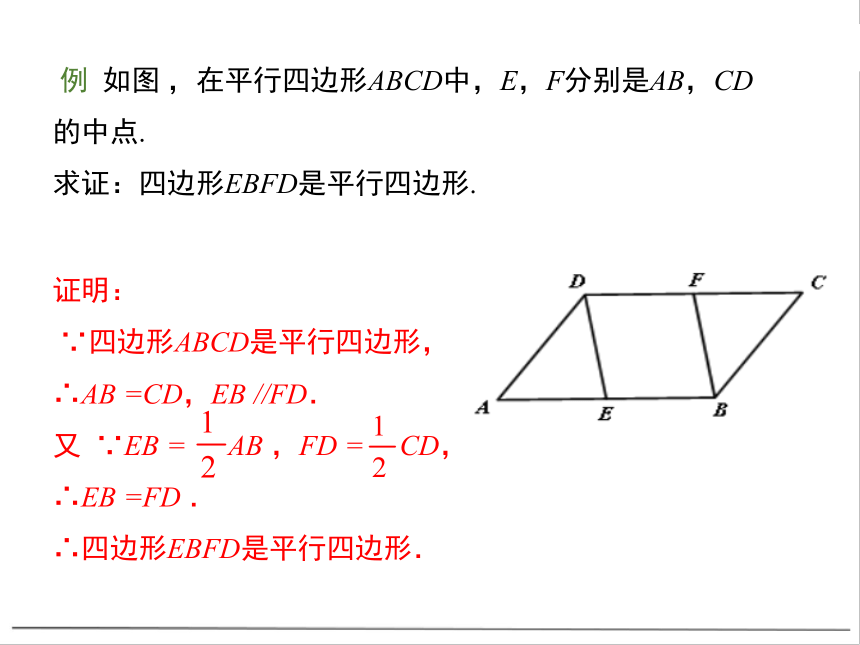
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
学以致用
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?
答:根据一组对边平行且相等的四边形是平行四边形可知,由枕木和铁轨构成的四边形是平行四边形,而平行四边形的对边平行,所以两条铁轨平行。
练一练
1.如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,四边形AEFD是平行四边形吗?为什么?
解:四边形AEFD是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
又∵E、F分别是边AB、CD的中点,
∴AE=DF.
又∵AE∥DF,
∴四边形AEFD是平行四边形.
练一练
2.已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点。
求证:BE=DF.
F
E
C
B
A
D
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED BF.
∥
﹦
∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
当堂练习
1.填空题: 如图,在四边形ABCD中,
①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。
②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。
③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
④如果AC、BD相交于点O,AC=8cm,BD=10cm,且AO___cm,DO=____cm,那么四边形ABCD是平行四边形。
8
4
60
120
60
6
4
5
A
B
C
D
A
B
C
D
O
2.四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形.
//
=
//
=
//
=
平行四边形AEFD和平行四边形EBCF有一条公共边EF,我们称它们是共边的两个平行四边形。根据平行四边形的性质非常容易得到AD BC.
提示
//
=
3.已知:如图,AD∥BC,且AB=CD=5,AC=4,BC=3;
求证:AB∥CD.
C
D
A
B
提示:可利用勾股定理及其逆定理解题
证明:∵在△ABC中,AB=5,AC=4,BC=3
∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°
∵ AD∥BC
∴∠DAC=∠ACB=90°
∵CD=5, AC=4,∴AD=3
∴AD∥BC 且AD=BC
∴四边形ABCD是平行四边形
∴ AB∥CD.
课堂小结
两组对边分别平行的四边形是平行四边形
平形四边形的判定
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
课后作业
18.1.2 平行四边形判定
第2课时 平行四边形的判定(2)
第十八章 平行四边形
讲授新课
当堂练习
课堂小结
学习目标
掌握用一组对边平行且相等来判定平行四边形的方法.
学习重点:平行四边形各种判定方法及应用,根据不同条件能正
确地选择判定方法.
学习难点:平行四边形的判定定理与性质定理的综合应用.
复习引入
边
1.一组对边分别平行的四边形是平行四边形(定义)
2.两组对边分别相等的四边形是平行四边形
角
两组对角分别相等的四边形是平行四边形
对角线
两条对角线互相平分的四边形是平行四边形
回顾与思考
回忆平行四边形的判定定理:
平形四边形的判定
讲授新课
平行四边形的判定定理4
将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?链接AD、BC,四边形ABCD是什么样的图形?
A
D
C
B
猜测:一组对边平行且相等的四边形是平行四边形
证一证
已知:四边形ABCD中 AB∥CD, AB=CD
求证: 四边形ABCD是平行四边形.
判定定理4:
一组对边平行且相等的四边形是平行四边形.
A
D
C
B
证明:连接BD.
∵AB∥CD,∴C
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .
又AB= CD,
∴四边形ABCD是平行四边形.
1
2
知识要点
判定定理4:一组对边平行且相等的四边形是平行四边形.书写:“ ”, 读作“平行且相等”.
A
B
C
D
ABCD
AD BC
几何语言:
在四边形ABCD中,
∵AB//CD,AB =CD, ∴四边形ABCD是平行四边形
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
学以致用
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?
答:根据一组对边平行且相等的四边形是平行四边形可知,由枕木和铁轨构成的四边形是平行四边形,而平行四边形的对边平行,所以两条铁轨平行。
练一练
1.如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,四边形AEFD是平行四边形吗?为什么?
解:四边形AEFD是平行四边形.理由如下:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
又∵E、F分别是边AB、CD的中点,
∴AE=DF.
又∵AE∥DF,
∴四边形AEFD是平行四边形.
练一练
2.已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点。
求证:BE=DF.
F
E
C
B
A
D
证明:
∵四边形ABCD是平行四边形,
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED BF.
∥
﹦
∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
当堂练习
1.填空题: 如图,在四边形ABCD中,
①如果AD=8cm,AB=4cm,且BC=____cm,CD=____cm,那么四边形ABCD是平行四边形。
②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。
③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
④如果AC、BD相交于点O,AC=8cm,BD=10cm,且AO___cm,DO=____cm,那么四边形ABCD是平行四边形。
8
4
60
120
60
6
4
5
A
B
C
D
A
B
C
D
O
2.四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形.
//
=
//
=
//
=
平行四边形AEFD和平行四边形EBCF有一条公共边EF,我们称它们是共边的两个平行四边形。根据平行四边形的性质非常容易得到AD BC.
提示
//
=
3.已知:如图,AD∥BC,且AB=CD=5,AC=4,BC=3;
求证:AB∥CD.
C
D
A
B
提示:可利用勾股定理及其逆定理解题
证明:∵在△ABC中,AB=5,AC=4,BC=3
∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°
∵ AD∥BC
∴∠DAC=∠ACB=90°
∵CD=5, AC=4,∴AD=3
∴AD∥BC 且AD=BC
∴四边形ABCD是平行四边形
∴ AB∥CD.
课堂小结
两组对边分别平行的四边形是平行四边形
平形四边形的判定
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
边
角
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
对角线
课后作业
