第19章一次函数的应用(一)课件(共15张PPT)
文档属性
| 名称 | 第19章一次函数的应用(一)课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 998.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:00:00 | ||
图片预览






文档简介
一次函数的应用(一)
教学目标:
1、熟练掌握求一次函数的解析式
的方法。
2、能构建一次函数模型,并用一次
函数关系式解决一些简单问题。
复习
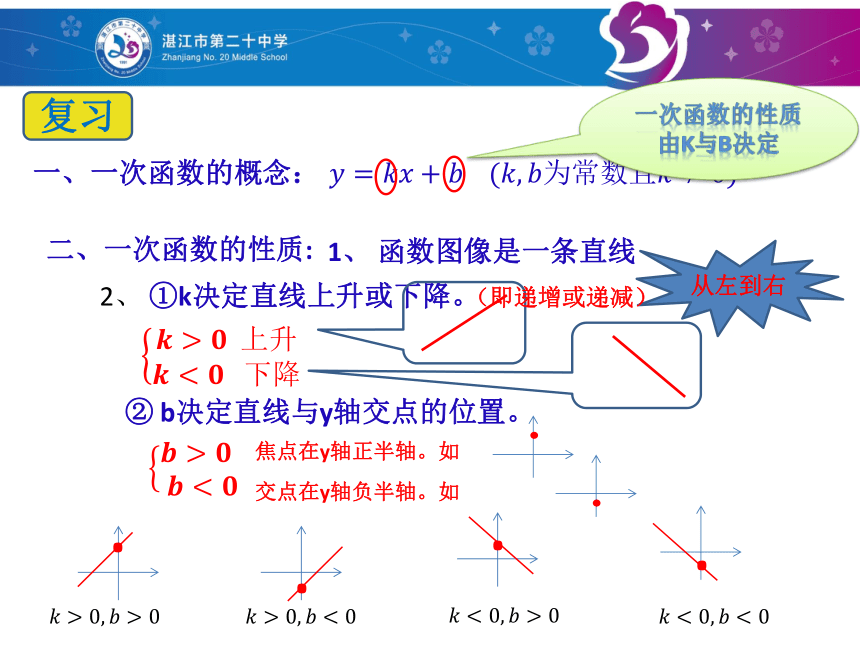
一、一次函数的概念:
二、一次函数的性质:
1、 函数图像是一条直线
????=????????+????????(????,????为常数且????≠0)
?
一次函数的性质由k与b决定
2、 ①k决定直线上升或下降。
????>??????上升?????
② b决定直线与y轴交点的位置。
????>???????????
焦点在y轴正半轴。如
交点在y轴负半轴。如
????>0,????>0
?
????>0,????<0
?
????<0,????>0
?
????<0,????<0
?
.
.
.
.
从左到右
(即递增或递减)
三、用待定系数法求一次函数解析式的一般步骤:
(1)设:根据已知条件设一次函数解析式????=????????+????
?
(4)回代:将求出的待定系数代回所求的一次函
数关系式中得出所求函数的解析式.
(2)代:将x、y的两对值或图象上的两个点的坐标代
入上述一次函数关系式中得到以待定系数为
未知 数二元一次的方程组;
(3)解:解二元一次方程得出未知系数的值;
新课学习
例1:已知弹簧的的长度????厘米在一定的限度内与所挂的重物质量????千克
?
是 一次函数的关系。且已知弹簧最大限重为10千克。现测得挂4千克
质量重物时候弹簧的长度14厘米,挂8千克质量的重物时弹簧的长度为16厘米。
(1)求这个一次函数的解析式,并写出自变量x的取值范围。
(2)求弹簧不挂重物时长度是多少厘米。
(3)当弹簧被拉长3厘米时,求所挂的重物的质量。
分析
①首先理解题目中y与x所表示的意义
②把题目的实际问题转化为数学语言
理解。
x=4,y=14
X=8,y=16
例1:已知弹簧的的长度????厘米在一定的限度内与所挂的重物质量????千克
?
是 一次函数的关系。且已知弹簧最大限重为10千克。现测得挂4千克
质量重物时候弹簧的长度14厘米,挂8千克质量的重物时弹簧的长度为16厘米。
(1)求这个一次函数的解析式,并写出自变量x的取值范围。
(2)求弹簧的原来长度是多少厘米。
(3)当弹簧被拉长3厘米时,求所挂的重物的质量。
解(1)设所求的一次函数解析式为y=kx+b,由已知的:
∴?4????+????=148????+????=16
?
????=12????=12
?
∴所求的一次函数的解析式为y=12x+12
?
(0≤????≤10)
?
x=4,y=14
X=8,y=16
新课学习
例1:已知弹簧的的长度????厘米在一定的限度内与所挂的重物质量????千克
?
是 一次函数的关系。且已知弹簧最大限重为10千克。现测得挂4千克
质量重物时候弹簧的长度14厘米,挂8千克质量的重物时弹簧的长度为16厘米。
(1)求这个一次函数的解析式,并写出自变量x的取值范围。
(2)求弹簧的原来长度是多少厘米。
(3)当弹簧被拉长3厘米时,求所挂的重物的质量。
弹黄原来的长度即是所挂重物质量x=0时y的值
(2) ∵ y=12x+12
?
∴ 当x=0,y=12
?
∴
?
弹黄原来的长度为12厘米。
?
(3)
∵ y=12x+12
?
∴ y=15时,即
?
12x+12=15
?
∴
?
x=6
∴
?
弹簧被拉长3厘米时,所挂的重物质量为6千克。
例2
放入3个小球后水面的高度升高6cm
2
水面的高度y随放入小球的数量x的变化而变化。
X=0,y=30
X=3,y=36
方法一:待定系数法
解:设一次函数的关系式为y=kx+b,
由已知得x=0时,y=30
x=3时,y=36
∴????=303????+????=36
?
解之的:
????=30????=????
?
∴
?
所求的一次函数关系式为y=2x+30
方法二:
每放入一个小球,水面高度y升高2cm
原来高度
后来高度y=原来高度+增加高度
y=
30
+2x
注满时即y=49时
当y=49时
即:30+2x=49
∴x=9.5
?
∴放入????????个小球时才有水溢出。
?
例3:某公司销售员的工资与每个月的销售量是一次函数关系。小李看见一张工资表如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售量(件)
……
8
10
工资(元)
……
4800
5800
你能帮小李解决如下问题吗?
(1)月最低工资(没有销售)标准是 元
(2)小李这个月销售量是15件,他的工资过万元了吗?
解:由已知可设工资y与销量X的 函数关系为:y=kx+b
把x=8,y=4800;x=10,y=5800代入得:
????????+????=????????????????????????????+????=????????????????
?
????=????????????????=????????????
?
∴y=500x+800
?
(1)当x=0时,y=800
(2)当x=15时,y=8300<10000
800
练习:
1、点燃一支新的蜡烛,燃烧后,剩下的蜡烛的高度h(厘米)
与燃烧时间t(小时)的函数图像如图所示:
(1)蜡烛的长度是 厘米,能燃烧 小时。
(2)蜡烛每小时燃烧 厘米。
(3)h与t 的函数关系式是
(4)燃烧 小时,蜡烛还剩下一半。
(5)燃烧4小时,蜡烛长度 厘米;燃烧6小时,蜡烛长度 厘米。
4
2.5
4
5
20
0
y=-4x+20 (0≤x≤5)
?
(0,20)
(5,0)
2.某电影院第一排有座位50个,后面一排座位数都比前面一排的座位数多2个。
(1)第10排的座位数是 个
(2)若第x排的是座位数为y个,则y与x的函数关系式为
50+10×????=70 正确吗?
?
×
50+2×(10-1)=68
68
y=
50+
2×(x-1)
y=2x+48
3.某省由于持续高温和连日无雨,水库蓄水量普遍下降,
如图所示是某水库蓄水量V(万立方米)与干旱时间t(天)之
间的关系图.请你根据此图填空:
(1)水库原蓄水量是________万立方米,干旱持续
10天,蓄水量为_______万立方米;
(2)若水库的蓄水量小于400万立方米时,将发出严重
干旱预报,则持续干旱_______天后,将发出严重
干旱预报.按此规律,持续干旱_______天时,
水库的水将干涸.
设:v=kx+b,把(10,800)(30,400)代入
30
800
1000
先求v与t的函数关系式
可求:v=-20x+1000,
V=0时,-20x+1000=0
t=50
50
小结:
1、弄清楚题目那两个变量x,y分别所表示的意义。
2、套入x,y的量把题目的实际问题转化为数学语言理解。
教学目标:
1、熟练掌握求一次函数的解析式
的方法。
2、能构建一次函数模型,并用一次
函数关系式解决一些简单问题。
复习
一、一次函数的概念:
二、一次函数的性质:
1、 函数图像是一条直线
????=????????+????????(????,????为常数且????≠0)
?
一次函数的性质由k与b决定
2、 ①k决定直线上升或下降。
????>??????上升?????
② b决定直线与y轴交点的位置。
????>???????????
焦点在y轴正半轴。如
交点在y轴负半轴。如
????>0,????>0
?
????>0,????<0
?
????<0,????>0
?
????<0,????<0
?
.
.
.
.
从左到右
(即递增或递减)
三、用待定系数法求一次函数解析式的一般步骤:
(1)设:根据已知条件设一次函数解析式????=????????+????
?
(4)回代:将求出的待定系数代回所求的一次函
数关系式中得出所求函数的解析式.
(2)代:将x、y的两对值或图象上的两个点的坐标代
入上述一次函数关系式中得到以待定系数为
未知 数二元一次的方程组;
(3)解:解二元一次方程得出未知系数的值;
新课学习
例1:已知弹簧的的长度????厘米在一定的限度内与所挂的重物质量????千克
?
是 一次函数的关系。且已知弹簧最大限重为10千克。现测得挂4千克
质量重物时候弹簧的长度14厘米,挂8千克质量的重物时弹簧的长度为16厘米。
(1)求这个一次函数的解析式,并写出自变量x的取值范围。
(2)求弹簧不挂重物时长度是多少厘米。
(3)当弹簧被拉长3厘米时,求所挂的重物的质量。
分析
①首先理解题目中y与x所表示的意义
②把题目的实际问题转化为数学语言
理解。
x=4,y=14
X=8,y=16
例1:已知弹簧的的长度????厘米在一定的限度内与所挂的重物质量????千克
?
是 一次函数的关系。且已知弹簧最大限重为10千克。现测得挂4千克
质量重物时候弹簧的长度14厘米,挂8千克质量的重物时弹簧的长度为16厘米。
(1)求这个一次函数的解析式,并写出自变量x的取值范围。
(2)求弹簧的原来长度是多少厘米。
(3)当弹簧被拉长3厘米时,求所挂的重物的质量。
解(1)设所求的一次函数解析式为y=kx+b,由已知的:
∴?4????+????=148????+????=16
?
????=12????=12
?
∴所求的一次函数的解析式为y=12x+12
?
(0≤????≤10)
?
x=4,y=14
X=8,y=16
新课学习
例1:已知弹簧的的长度????厘米在一定的限度内与所挂的重物质量????千克
?
是 一次函数的关系。且已知弹簧最大限重为10千克。现测得挂4千克
质量重物时候弹簧的长度14厘米,挂8千克质量的重物时弹簧的长度为16厘米。
(1)求这个一次函数的解析式,并写出自变量x的取值范围。
(2)求弹簧的原来长度是多少厘米。
(3)当弹簧被拉长3厘米时,求所挂的重物的质量。
弹黄原来的长度即是所挂重物质量x=0时y的值
(2) ∵ y=12x+12
?
∴ 当x=0,y=12
?
∴
?
弹黄原来的长度为12厘米。
?
(3)
∵ y=12x+12
?
∴ y=15时,即
?
12x+12=15
?
∴
?
x=6
∴
?
弹簧被拉长3厘米时,所挂的重物质量为6千克。
例2
放入3个小球后水面的高度升高6cm
2
水面的高度y随放入小球的数量x的变化而变化。
X=0,y=30
X=3,y=36
方法一:待定系数法
解:设一次函数的关系式为y=kx+b,
由已知得x=0时,y=30
x=3时,y=36
∴????=303????+????=36
?
解之的:
????=30????=????
?
∴
?
所求的一次函数关系式为y=2x+30
方法二:
每放入一个小球,水面高度y升高2cm
原来高度
后来高度y=原来高度+增加高度
y=
30
+2x
注满时即y=49时
当y=49时
即:30+2x=49
∴x=9.5
?
∴放入????????个小球时才有水溢出。
?
例3:某公司销售员的工资与每个月的销售量是一次函数关系。小李看见一张工资表如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售量(件)
……
8
10
工资(元)
……
4800
5800
你能帮小李解决如下问题吗?
(1)月最低工资(没有销售)标准是 元
(2)小李这个月销售量是15件,他的工资过万元了吗?
解:由已知可设工资y与销量X的 函数关系为:y=kx+b
把x=8,y=4800;x=10,y=5800代入得:
????????+????=????????????????????????????+????=????????????????
?
????=????????????????=????????????
?
∴y=500x+800
?
(1)当x=0时,y=800
(2)当x=15时,y=8300<10000
800
练习:
1、点燃一支新的蜡烛,燃烧后,剩下的蜡烛的高度h(厘米)
与燃烧时间t(小时)的函数图像如图所示:
(1)蜡烛的长度是 厘米,能燃烧 小时。
(2)蜡烛每小时燃烧 厘米。
(3)h与t 的函数关系式是
(4)燃烧 小时,蜡烛还剩下一半。
(5)燃烧4小时,蜡烛长度 厘米;燃烧6小时,蜡烛长度 厘米。
4
2.5
4
5
20
0
y=-4x+20 (0≤x≤5)
?
(0,20)
(5,0)
2.某电影院第一排有座位50个,后面一排座位数都比前面一排的座位数多2个。
(1)第10排的座位数是 个
(2)若第x排的是座位数为y个,则y与x的函数关系式为
50+10×????=70 正确吗?
?
×
50+2×(10-1)=68
68
y=
50+
2×(x-1)
y=2x+48
3.某省由于持续高温和连日无雨,水库蓄水量普遍下降,
如图所示是某水库蓄水量V(万立方米)与干旱时间t(天)之
间的关系图.请你根据此图填空:
(1)水库原蓄水量是________万立方米,干旱持续
10天,蓄水量为_______万立方米;
(2)若水库的蓄水量小于400万立方米时,将发出严重
干旱预报,则持续干旱_______天后,将发出严重
干旱预报.按此规律,持续干旱_______天时,
水库的水将干涸.
设:v=kx+b,把(10,800)(30,400)代入
30
800
1000
先求v与t的函数关系式
可求:v=-20x+1000,
V=0时,-20x+1000=0
t=50
50
小结:
1、弄清楚题目那两个变量x,y分别所表示的意义。
2、套入x,y的量把题目的实际问题转化为数学语言理解。
