19.1.1 变量与函数 课件(共23张ppt)
文档属性
| 名称 | 19.1.1 变量与函数 课件(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 588.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:00:00 | ||
图片预览








文档简介
19.1.1变量与函数
教 学 目 标
1.认识函数,理解函数、常量、变量、自变量的意义。
2.弄清楚函数的三中表示方法。
3.学列函数解析式,会写自变量的取值范围。
4.运用函数定义及表示方法解决实际问题。
变量与函数
大千世界处在不停的运动变化之中,如何 来研究这些运动变化并寻找规律呢?
数学上常用函数来刻画各种运动变化.
在日常学习和生活中,我们常要研究一些数量关系:
小明到商店买练习簿,每本单价2元,
购买的总数x(本)与总金额y(元)的关系式,
可以表示为
其中y随x的变化而变化
y=2x
这个式子中的y与x成比例吗?是什么比例?
在这中间,哪些量是不确定的、会发生变化?
哪些又是确定不变的呢?
创设情境:
在某一变化过程中,可以取不同数值
的量,叫做变量。
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量。
1、定义:
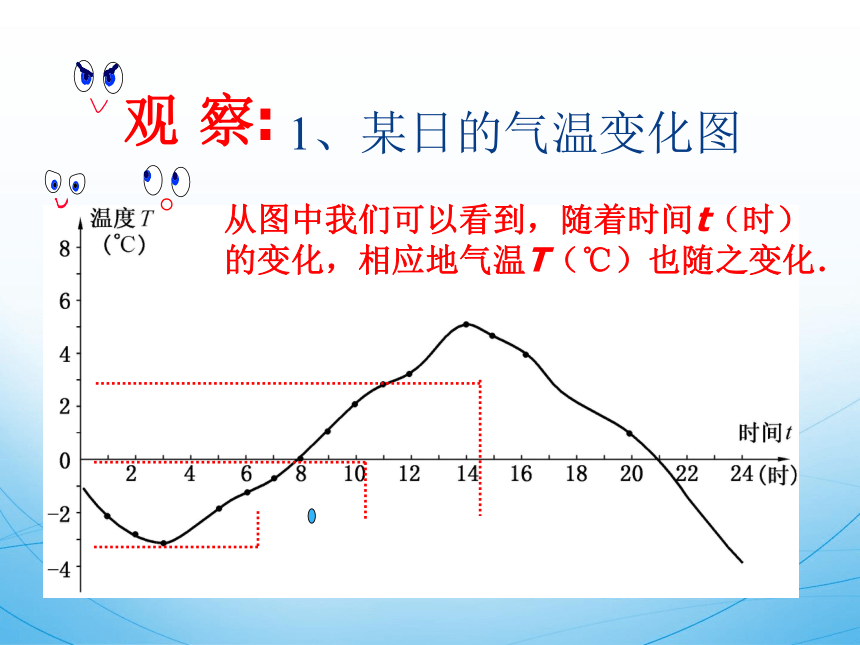
1、某日的气温变化图
从图中我们可以看到,随着时间t(时)
的变化,相应地气温T(℃)也随之变化.
观 察:
2、 2002年7月中国工商银行为
“整存整取”的存款方式规定的利率
观察上表,说说随着存期x的增长,
相应的利率y是如何变化的.
观 察:
你还能举出一些像这样一个量随着另一个量的变化而变化的实例吗?能指出其中的常量和变量吗?
畅所欲言
一般地,在一个变化过程中有两个变量x与y,如果对于x每 一个值,y都有唯一的值与它对应,那么就说x是自变量,y是因变量,此时也称 y是x的函数。
1、定义:
试一试:看谁的眼光准!
经典例题1:判断下列变量关系是不是函数?
判断是不是函数,我们可以看它的数学式子中的变量之间是否满足函数的定义
注意:函数与自变量之间是一种对应关系,并且要求对于x的每一个值、y都有唯一的值与之相对应。
(1) xy=2;
(3) x+y=5;
(5) y=x2-4x+5
(2) x2+y2=10;
(4) |y|=x;
(6) y= |x|
指出下列变化关系中,哪些y是x的函数,哪些不是?说出你的理由。
是
否
是
是
否
是
该你显身手了!
表示函数关系的方法通常有三种:
?
(1) 解析式法,如 。?
(2) 列表法,如 。
(3) 图象法,如 。
2、表示函数关系的方法:
y=2x
观察2中的利率表
观察1中的气温曲线
(用数学式子表示函数与自变量之间关系的方法叫解析式法)
经典例题2,求自变量取值范围:
(1)y=x
例1:
一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中油量y(L)随行驶里程x(km)的增加而减少,平均耗油量为0.1L/km
问题1:写出表示y与x的函数关系的式子
问题2:指出自变量x的取值范围。
问题3:汽车行驶200km时,油箱中还有多少汽油?
注意:自变量的取值范围从两个方面来判断
1、还要考虑函数关系式不能无意义
2、实际问题要以实际情况来定
(1)y=2x+3
写出自变量的取值范围
请同学们想一想函数自变量的取值范围有什么规律?
(1)有分母,分母不能为零
(4)是实际问题,要使实际问题有意义
(3)零次幂,底数不能为零
(2)开偶数次方,被开方数是非负数
方法归纳:
?(1)圆的周长C与半径r的关系式;
(2)火车以60千米/时的速度行驶,它 驶过的路程
s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.
写出下列各问题中的关系式,并指出常量、变量
经典例题3、如何书写函数关系式呢?
1、y 比 x的 少2
2、y 是 x的 倒数的4倍
根据所给的 条件,写出y与x的函数关系式:
3、矩形的周长是18 cm ,它的长是y,
宽是x cm ;
实战练练吧!
本节课我们学习主要内容是什么?
你有什么收获?
课堂小结:
课堂检测:
1、在y=3x+1中,如果x 是自变量, 是x的函数
2、下列说法中,不正确的是( )
A、函数不是数,而是 一种关系
B、多边形的内角和是边数的函数
C、一天中时间是温度的函数
D、一天中温度是时间的函数
3、正方形的边长为5 cm,当边长减少x cm时,周长为y cm,求y与x的函数关系式,并写出自变量x的取值范围。
共同探讨
4、已知等腰三角形ABC的底边AB的长为4,腰AC的长X在变化着,三角形ABC的周长为L.
求 L关于X的函数解析式.
(2)写出自变量的取值范围。
某汽车的油箱内装有30 公升的油,行驶时每百公里耗油2.5公升,设行使的里程为X(百公里),求油箱中所剩下的油 y (公升)与x之间的函数关系式?
课后提升:
当x=10时,y=?
当x=12.1时,y=?
当x=12时,y=?
教 学 目 标
1.认识函数,理解函数、常量、变量、自变量的意义。
2.弄清楚函数的三中表示方法。
3.学列函数解析式,会写自变量的取值范围。
4.运用函数定义及表示方法解决实际问题。
变量与函数
大千世界处在不停的运动变化之中,如何 来研究这些运动变化并寻找规律呢?
数学上常用函数来刻画各种运动变化.
在日常学习和生活中,我们常要研究一些数量关系:
小明到商店买练习簿,每本单价2元,
购买的总数x(本)与总金额y(元)的关系式,
可以表示为
其中y随x的变化而变化
y=2x
这个式子中的y与x成比例吗?是什么比例?
在这中间,哪些量是不确定的、会发生变化?
哪些又是确定不变的呢?
创设情境:
在某一变化过程中,可以取不同数值
的量,叫做变量。
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量。
1、定义:
1、某日的气温变化图
从图中我们可以看到,随着时间t(时)
的变化,相应地气温T(℃)也随之变化.
观 察:
2、 2002年7月中国工商银行为
“整存整取”的存款方式规定的利率
观察上表,说说随着存期x的增长,
相应的利率y是如何变化的.
观 察:
你还能举出一些像这样一个量随着另一个量的变化而变化的实例吗?能指出其中的常量和变量吗?
畅所欲言
一般地,在一个变化过程中有两个变量x与y,如果对于x每 一个值,y都有唯一的值与它对应,那么就说x是自变量,y是因变量,此时也称 y是x的函数。
1、定义:
试一试:看谁的眼光准!
经典例题1:判断下列变量关系是不是函数?
判断是不是函数,我们可以看它的数学式子中的变量之间是否满足函数的定义
注意:函数与自变量之间是一种对应关系,并且要求对于x的每一个值、y都有唯一的值与之相对应。
(1) xy=2;
(3) x+y=5;
(5) y=x2-4x+5
(2) x2+y2=10;
(4) |y|=x;
(6) y= |x|
指出下列变化关系中,哪些y是x的函数,哪些不是?说出你的理由。
是
否
是
是
否
是
该你显身手了!
表示函数关系的方法通常有三种:
?
(1) 解析式法,如 。?
(2) 列表法,如 。
(3) 图象法,如 。
2、表示函数关系的方法:
y=2x
观察2中的利率表
观察1中的气温曲线
(用数学式子表示函数与自变量之间关系的方法叫解析式法)
经典例题2,求自变量取值范围:
(1)y=x
例1:
一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中油量y(L)随行驶里程x(km)的增加而减少,平均耗油量为0.1L/km
问题1:写出表示y与x的函数关系的式子
问题2:指出自变量x的取值范围。
问题3:汽车行驶200km时,油箱中还有多少汽油?
注意:自变量的取值范围从两个方面来判断
1、还要考虑函数关系式不能无意义
2、实际问题要以实际情况来定
(1)y=2x+3
写出自变量的取值范围
请同学们想一想函数自变量的取值范围有什么规律?
(1)有分母,分母不能为零
(4)是实际问题,要使实际问题有意义
(3)零次幂,底数不能为零
(2)开偶数次方,被开方数是非负数
方法归纳:
?(1)圆的周长C与半径r的关系式;
(2)火车以60千米/时的速度行驶,它 驶过的路程
s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.
写出下列各问题中的关系式,并指出常量、变量
经典例题3、如何书写函数关系式呢?
1、y 比 x的 少2
2、y 是 x的 倒数的4倍
根据所给的 条件,写出y与x的函数关系式:
3、矩形的周长是18 cm ,它的长是y,
宽是x cm ;
实战练练吧!
本节课我们学习主要内容是什么?
你有什么收获?
课堂小结:
课堂检测:
1、在y=3x+1中,如果x 是自变量, 是x的函数
2、下列说法中,不正确的是( )
A、函数不是数,而是 一种关系
B、多边形的内角和是边数的函数
C、一天中时间是温度的函数
D、一天中温度是时间的函数
3、正方形的边长为5 cm,当边长减少x cm时,周长为y cm,求y与x的函数关系式,并写出自变量x的取值范围。
共同探讨
4、已知等腰三角形ABC的底边AB的长为4,腰AC的长X在变化着,三角形ABC的周长为L.
求 L关于X的函数解析式.
(2)写出自变量的取值范围。
某汽车的油箱内装有30 公升的油,行驶时每百公里耗油2.5公升,设行使的里程为X(百公里),求油箱中所剩下的油 y (公升)与x之间的函数关系式?
课后提升:
当x=10时,y=?
当x=12.1时,y=?
当x=12时,y=?
