17.1勾股定理的应用 课件(共15张PPT)
文档属性
| 名称 | 17.1勾股定理的应用 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 632.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:00:00 | ||
图片预览





文档简介
勾股定理的应用
在学习的过程中注意理论与实际问题的联系;
能利用勾股定理和勾股定理逆定理解决实际问题;
通过学习提高同学们的空间想象能力.
A
B
一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
C
D
了解下面题目,
重点了解怎样利用课本
知识解决实际问题.
我怎么走
会最近呢?
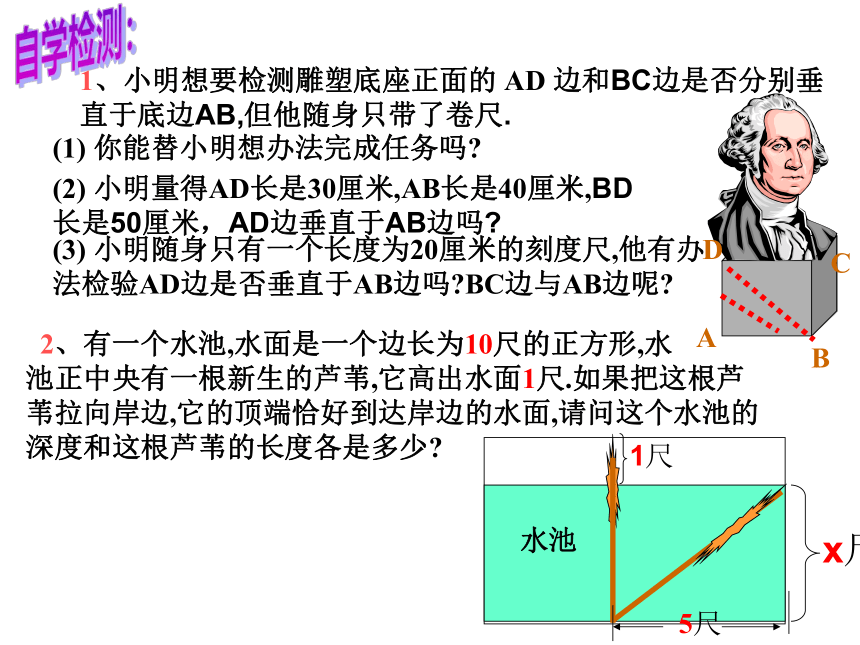
1、小明想要检测雕塑底座正面的 AD 边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
(1) 你能替小明想办法完成任务吗?
(2) 小明量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?
(3) 小明随身只有一个长度为20厘米的刻度尺,他有办
法检验AD边是否垂直于AB边吗?BC边与AB边呢?
A
B
C
D
2、有一个水池,水面是一个边长为10尺的正方形,水 池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
水池
1尺
5尺
x尺
(2)李叔叔量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?为什么?
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺,
(1)你能替他想办法完成任务吗?
∴AD和AB垂直
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺,
(1)你能替他想办法完成任务吗?
(2)李叔叔量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?为什么?
(3)小明随身只有一个长度为20厘米的刻度尺,他能有办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
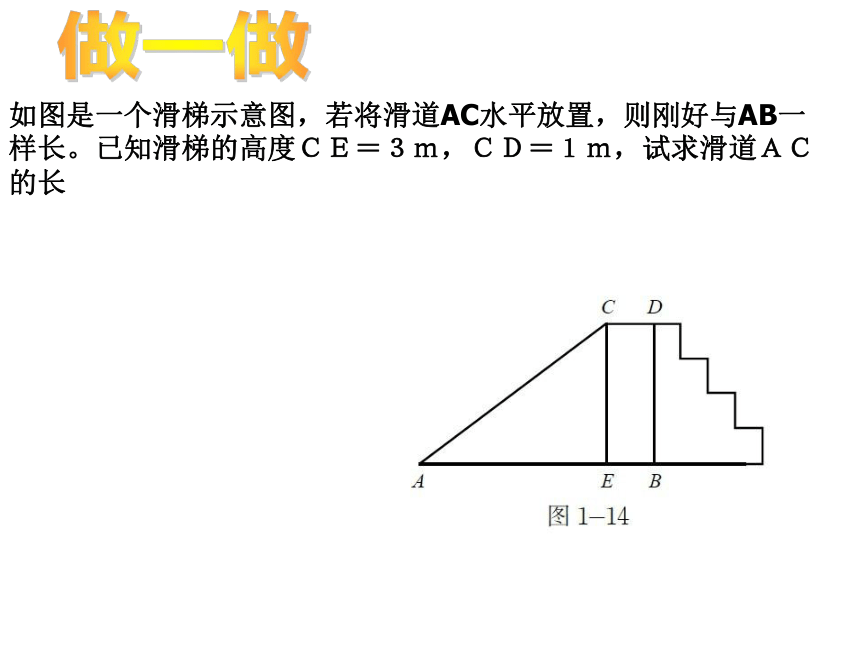
如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长。已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长
有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
最短是多少米?
小试牛刀
甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走。上午10:00,甲、乙两人相距多远?
检测训练
1.有一只蚂蚁从一个正方体的顶点A
沿表面爬到顶点C,如果底面是一
个边长为4厘米的正方形,高为6厘
米,则蚂蚁所爬的最短路径是多少
厘米?
A
C
2.在一棵树的10米高处B有两只猴子,
其中一只猴子爬下树走到离树20米的
池塘A,另一只猴子爬到树顶D后直接
跃向池塘的A处,如果两只猴子所经过
距离相等,试问这棵树有多高?
.
D
B
C
A
3 如图所示,有一个圆柱,它的高是12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行到B点,求其爬行的最短路程是多少?
2、注意:运用勾股定理解决实际问题时,
①、没有图的要按题意画好图并标上字母;
②、有时必须设好未知数,并根据勾股定理列出相应的方程式才能做出答案。
归纳总结
1、数学思想:
数学问题
转化
实际问题
作业:
课本习题 1、3.
再见
在学习的过程中注意理论与实际问题的联系;
能利用勾股定理和勾股定理逆定理解决实际问题;
通过学习提高同学们的空间想象能力.
A
B
一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
C
D
了解下面题目,
重点了解怎样利用课本
知识解决实际问题.
我怎么走
会最近呢?
1、小明想要检测雕塑底座正面的 AD 边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
(1) 你能替小明想办法完成任务吗?
(2) 小明量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?
(3) 小明随身只有一个长度为20厘米的刻度尺,他有办
法检验AD边是否垂直于AB边吗?BC边与AB边呢?
A
B
C
D
2、有一个水池,水面是一个边长为10尺的正方形,水 池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
水池
1尺
5尺
x尺
(2)李叔叔量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?为什么?
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺,
(1)你能替他想办法完成任务吗?
∴AD和AB垂直
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺,
(1)你能替他想办法完成任务吗?
(2)李叔叔量得AD长是30厘米,AB长是40厘米,BD长是50厘米,AD边垂直于AB边吗?为什么?
(3)小明随身只有一个长度为20厘米的刻度尺,他能有办法检验AD边是否垂直于AB边吗?BC边与AB边呢?
如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长。已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长
有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
最短是多少米?
小试牛刀
甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走。上午10:00,甲、乙两人相距多远?
检测训练
1.有一只蚂蚁从一个正方体的顶点A
沿表面爬到顶点C,如果底面是一
个边长为4厘米的正方形,高为6厘
米,则蚂蚁所爬的最短路径是多少
厘米?
A
C
2.在一棵树的10米高处B有两只猴子,
其中一只猴子爬下树走到离树20米的
池塘A,另一只猴子爬到树顶D后直接
跃向池塘的A处,如果两只猴子所经过
距离相等,试问这棵树有多高?
.
D
B
C
A
3 如图所示,有一个圆柱,它的高是12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行到B点,求其爬行的最短路程是多少?
2、注意:运用勾股定理解决实际问题时,
①、没有图的要按题意画好图并标上字母;
②、有时必须设好未知数,并根据勾股定理列出相应的方程式才能做出答案。
归纳总结
1、数学思想:
数学问题
转化
实际问题
作业:
课本习题 1、3.
再见
