18.1.2平行四边形的判定 课件(共15张PPT)
文档属性
| 名称 | 18.1.2平行四边形的判定 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 850.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 09:16:22 | ||
图片预览


文档简介
第十八章
四边形
18.1平行四边形的判定(1)
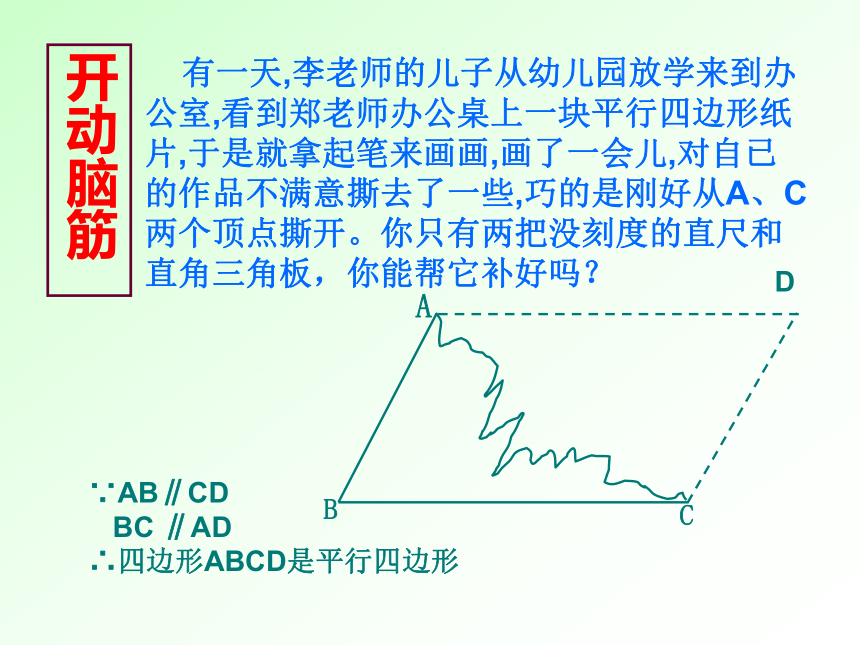
开动脑筋
有一天,李老师的儿子从幼儿园放学来到办公室,看到郑老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。你只有两把没刻度的直尺和直角三角板,你能帮它补好吗?
A
B
C
D
∵AB∥CD
BC
∥AD
∴四边形ABCD是平行四边形
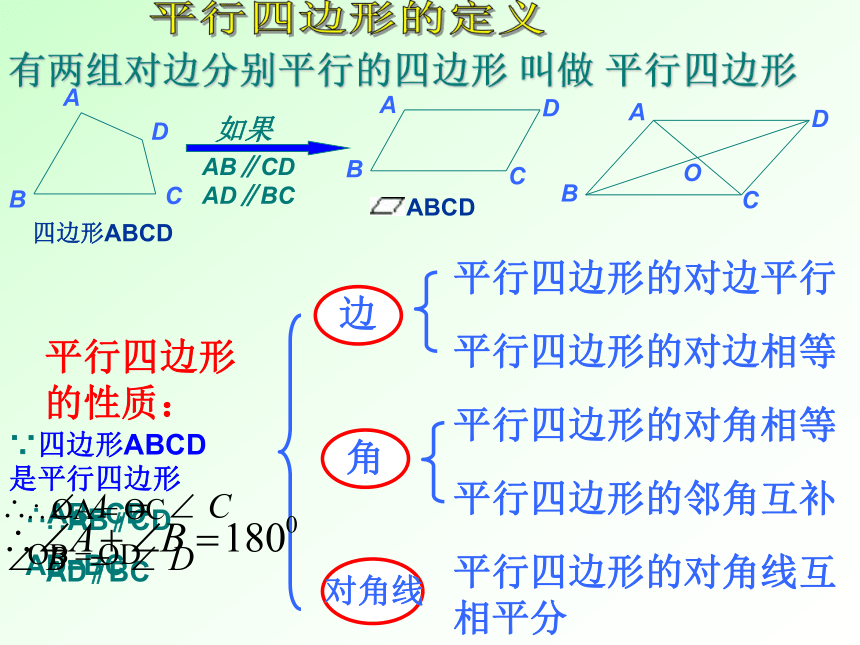
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD
是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
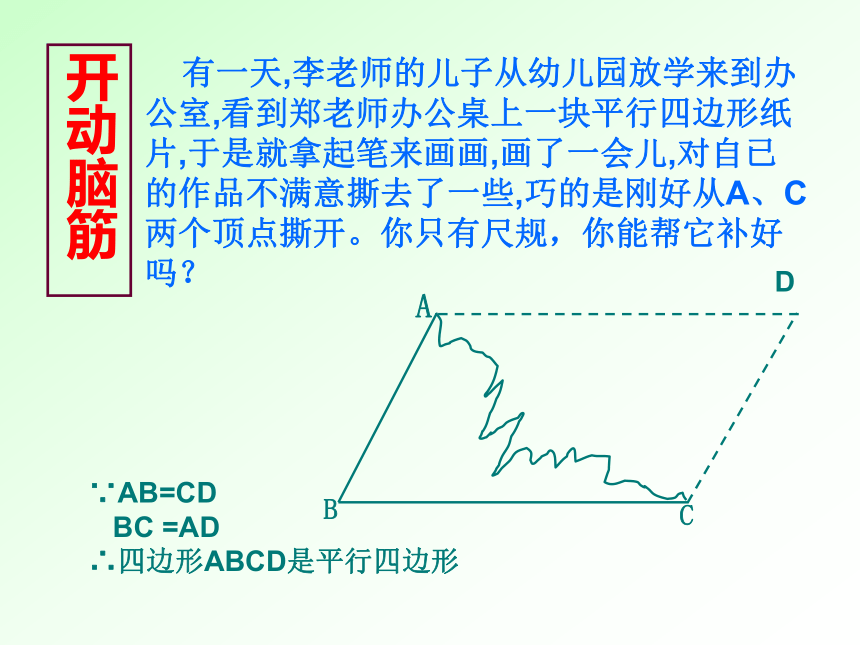
开动脑筋
有一天,李老师的儿子从幼儿园放学来到办公室,看到郑老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。你只有尺规,你能帮它补好吗?
A
B
C
D
∵AB=CD
BC
=AD
∴四边形ABCD是平行四边形
B
C
A
D
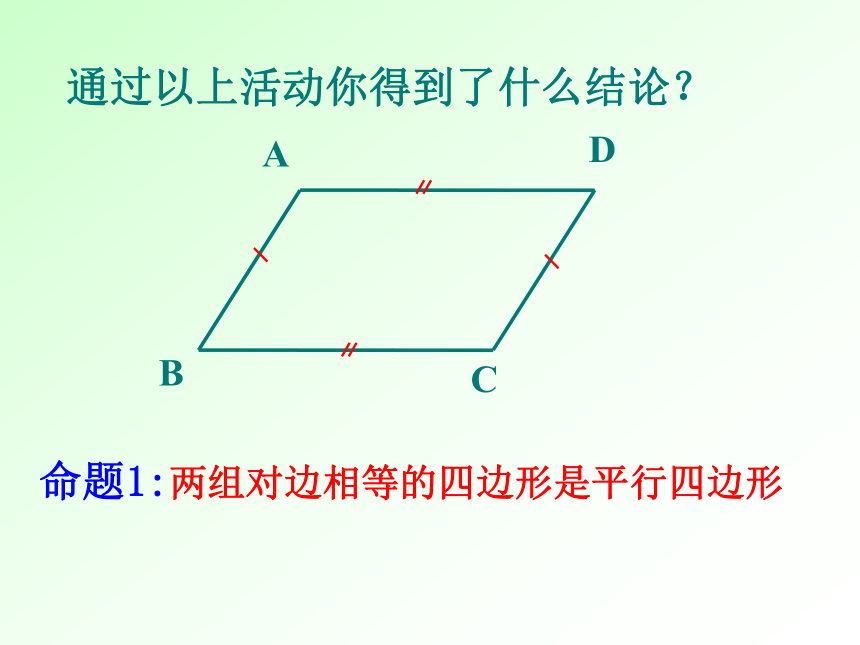
通过以上活动你得到了什么结论?
命题1:两组对边相等的四边形是平行四边形
B
D
A
C
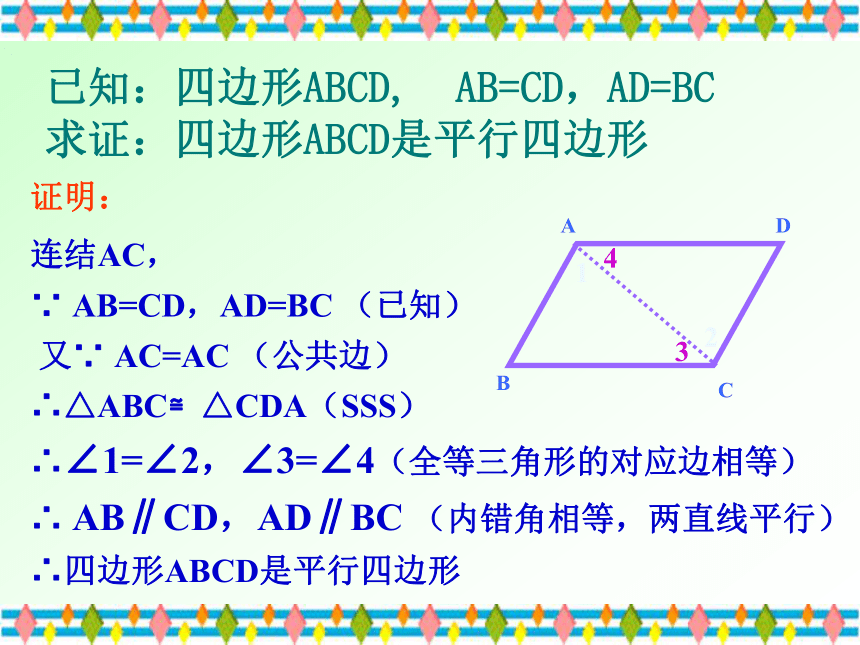
已知:四边形ABCD,
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
2
1
3
4
连结AC,
∵
AB=CD,AD=BC
(已知)
又∵
AC=AC
(公共边)
∴△ABC≌△CDA(SSS)
证明:
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴
AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两
组对边分别相等的四边形是平行四边形。)
如图,AB
=DC=EF,
AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB
∥
DC∥
EF
AD
∥
BC
DE
∥
CF
学行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
B
D
A
C
∠A+
∠B=180
°
AD∥BC
小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形
ABCD
∠A+
∠D=180
°
AB∥CD
∠A+
∠B
+∠C+
∠D
=360
°
B
D
A
C
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+
∠B+
∠C+
∠D
=360
°
∴
2∠A+
2∠B=360
°
证明:
即∠A+
∠B=180
°
∴
AD∥BC
(同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形。
A
B
C
D
∵
∠A=∠C,
∠B=∠D
(已知)
∴四边形ABCD是平行四边形(两
组对角分别相等的四边形是平行四边形。)
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
定理1
两组对边分别相等的四边形是平行四边形
∵AB=CD,
AD=
BC
∴…是平行四边形
定理2
两组对角分别相等的四边形是平行四边形
∵∠A=∠C,
∠B=∠D
∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
再见
四边形
18.1平行四边形的判定(1)
开动脑筋
有一天,李老师的儿子从幼儿园放学来到办公室,看到郑老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。你只有两把没刻度的直尺和直角三角板,你能帮它补好吗?
A
B
C
D
∵AB∥CD
BC
∥AD
∴四边形ABCD是平行四边形
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD
是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
开动脑筋
有一天,李老师的儿子从幼儿园放学来到办公室,看到郑老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。你只有尺规,你能帮它补好吗?
A
B
C
D
∵AB=CD
BC
=AD
∴四边形ABCD是平行四边形
B
C
A
D
通过以上活动你得到了什么结论?
命题1:两组对边相等的四边形是平行四边形
B
D
A
C
已知:四边形ABCD,
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
2
1
3
4
连结AC,
∵
AB=CD,AD=BC
(已知)
又∵
AC=AC
(公共边)
∴△ABC≌△CDA(SSS)
证明:
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴
AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两
组对边分别相等的四边形是平行四边形。)
如图,AB
=DC=EF,
AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB
∥
DC∥
EF
AD
∥
BC
DE
∥
CF
学行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
B
D
A
C
∠A+
∠B=180
°
AD∥BC
小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形
ABCD
∠A+
∠D=180
°
AB∥CD
∠A+
∠B
+∠C+
∠D
=360
°
B
D
A
C
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+
∠B+
∠C+
∠D
=360
°
∴
2∠A+
2∠B=360
°
证明:
即∠A+
∠B=180
°
∴
AD∥BC
(同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形。
A
B
C
D
∵
∠A=∠C,
∠B=∠D
(已知)
∴四边形ABCD是平行四边形(两
组对角分别相等的四边形是平行四边形。)
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
定理1
两组对边分别相等的四边形是平行四边形
∵AB=CD,
AD=
BC
∴…是平行四边形
定理2
两组对角分别相等的四边形是平行四边形
∵∠A=∠C,
∠B=∠D
∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
再见
