29.2 由三视图到表面展开图(第3课时) 课件(共17张PPT)
文档属性
| 名称 | 29.2 由三视图到表面展开图(第3课时) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 616.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:00:00 | ||
图片预览


文档简介
第二十九章 投影与视图
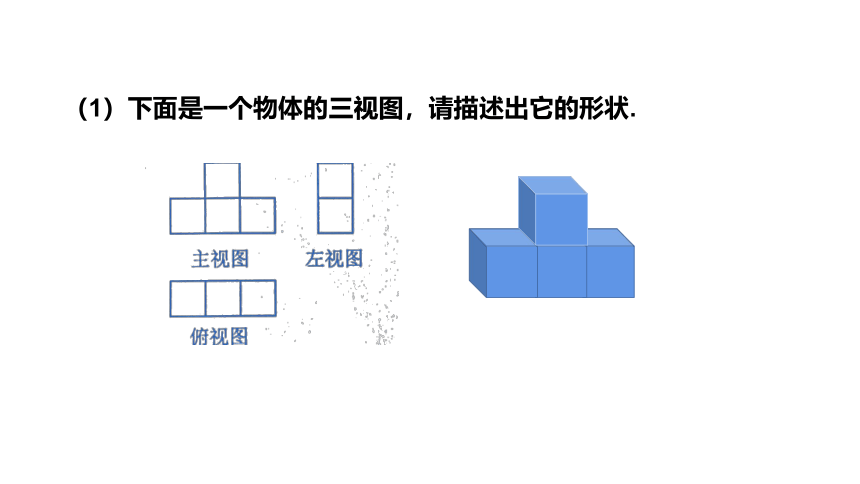
(1)下面是一个物体的三视图,请描述出它的形状.
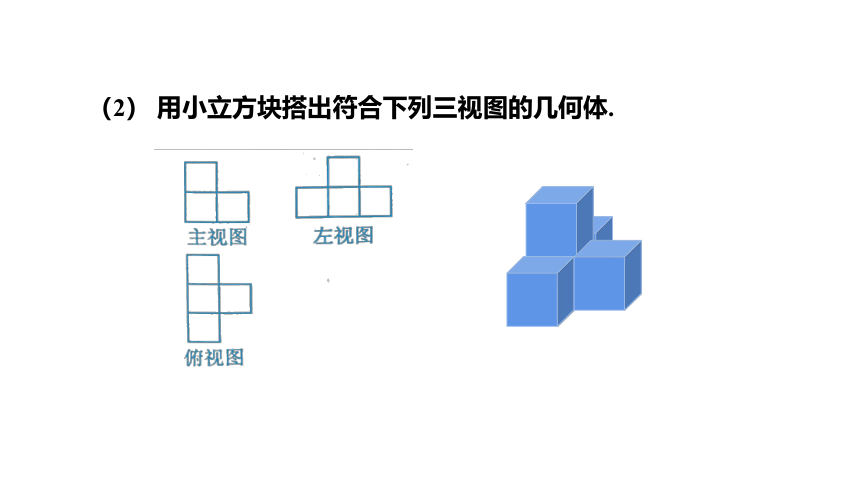
(2) 用小立方块搭出符合下列三视图的几何体.
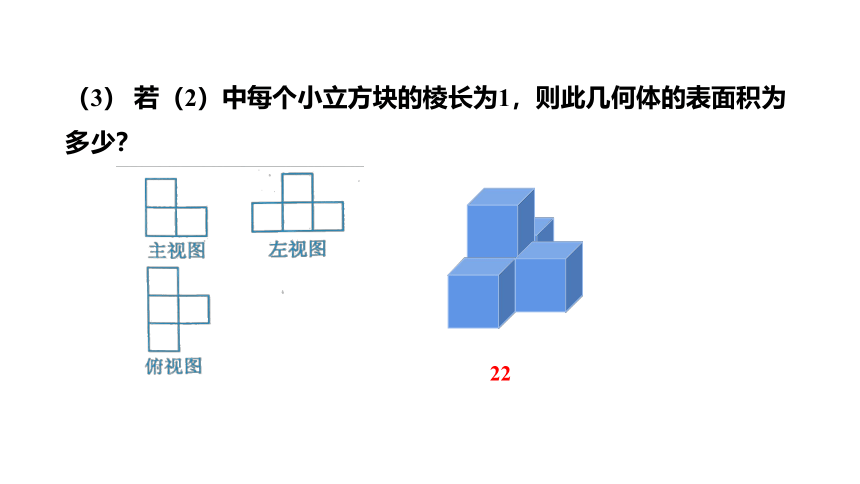
(3) 若(2)中每个小立方块的棱长为1,则此几何体的表面积为多少?
22
探究体验
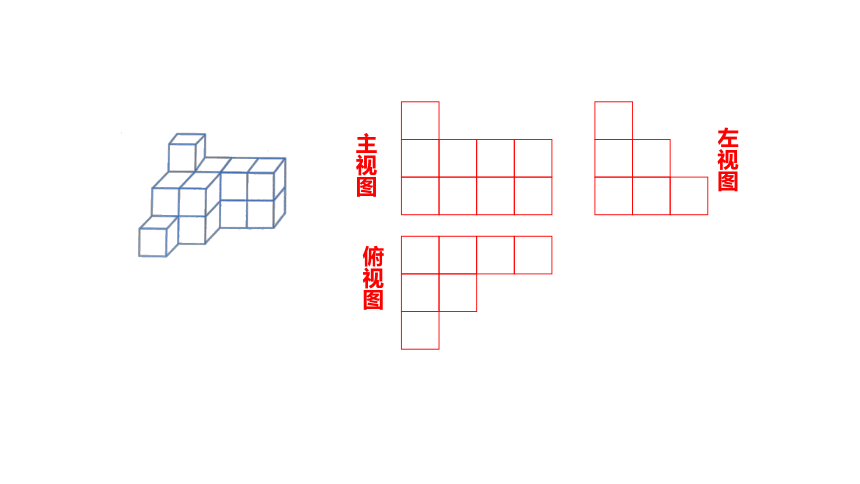
(1)下图中的几何体有多少个小立方块?请画出它的三视图.
主视图
左视图
俯视图
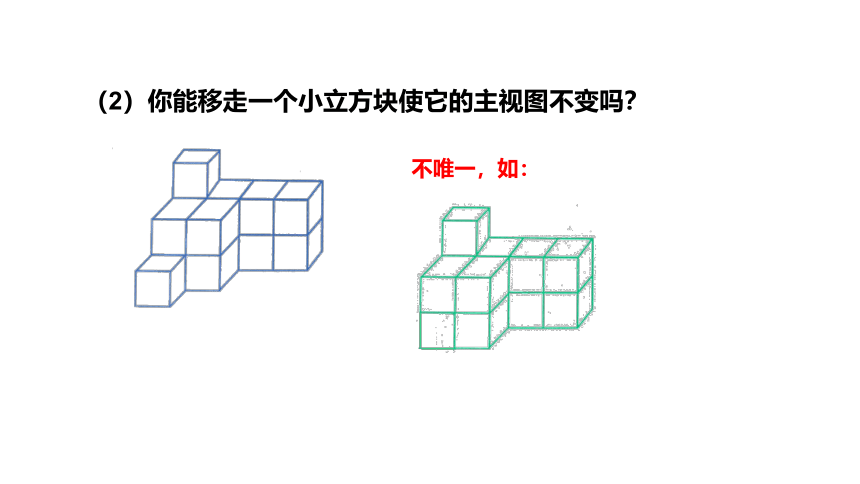
(2)你能移走一个小立方块使它的主视图不变吗?
不唯一,如:
(3)你能移走一个小立方块使它的三视图不变吗?
如图:
应用
例1 某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如图),请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).
解:由三视图可知,密封罐的形状是正六棱柱(如下图中左图).
密封罐的高为50 mm,底面正六边形的对角线为100 mm,边长为50 mm,下图中右图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为:
例2 根据下面的三视图请说出建筑物模型是什么样子的,共有几层?一共需要多少个小正方体?
解:该建筑物模型的形状如下图所示:
有3层,共需要9个小正方体.
巩固练习
1.根据下列几何体的三视图,画出它们的展开图.
解:该几何体是三棱柱,展开图如下:
解:该几何体是圆柱,展开图如下:
2.某工厂加工一批无底帐篷,设计者给出了帐篷的三视图.请你按照三视图确定每顶帐篷的表面积(图中尺寸单位:cm)
240
200
300
解:该几何体是由下面是圆柱、上面是圆锥组成的几何体,表面积为:
(1)下面是一个物体的三视图,请描述出它的形状.
(2) 用小立方块搭出符合下列三视图的几何体.
(3) 若(2)中每个小立方块的棱长为1,则此几何体的表面积为多少?
22
探究体验
(1)下图中的几何体有多少个小立方块?请画出它的三视图.
主视图
左视图
俯视图
(2)你能移走一个小立方块使它的主视图不变吗?
不唯一,如:
(3)你能移走一个小立方块使它的三视图不变吗?
如图:
应用
例1 某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如图),请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm).
解:由三视图可知,密封罐的形状是正六棱柱(如下图中左图).
密封罐的高为50 mm,底面正六边形的对角线为100 mm,边长为50 mm,下图中右图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为:
例2 根据下面的三视图请说出建筑物模型是什么样子的,共有几层?一共需要多少个小正方体?
解:该建筑物模型的形状如下图所示:
有3层,共需要9个小正方体.
巩固练习
1.根据下列几何体的三视图,画出它们的展开图.
解:该几何体是三棱柱,展开图如下:
解:该几何体是圆柱,展开图如下:
2.某工厂加工一批无底帐篷,设计者给出了帐篷的三视图.请你按照三视图确定每顶帐篷的表面积(图中尺寸单位:cm)
240
200
300
解:该几何体是由下面是圆柱、上面是圆锥组成的几何体,表面积为:
