28.2.1: 解直角三角形 课件(共14张PPT)
文档属性
| 名称 | 28.2.1: 解直角三角形 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 703.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 08:39:24 | ||
图片预览






文档简介
28.2 解直角三角形及其应用
28.2.1 解直角三角形
1.使学生理解直角三角形中六个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
2.渗透数形结合的数学思想,培养学生良好的学习习惯.
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____.
(2)锐角之间的关系:∠A+∠B=_____.
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
利用计算器可得 .
根据以上条件可以求出塔身中心线与垂直中
心线的夹角.你愿意试着计算一下吗?
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过点B向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
A
B
C
将上述问题推广到一般情形,就是:已知直角
三角形的斜边和一条直角边,求它的锐角的度数.
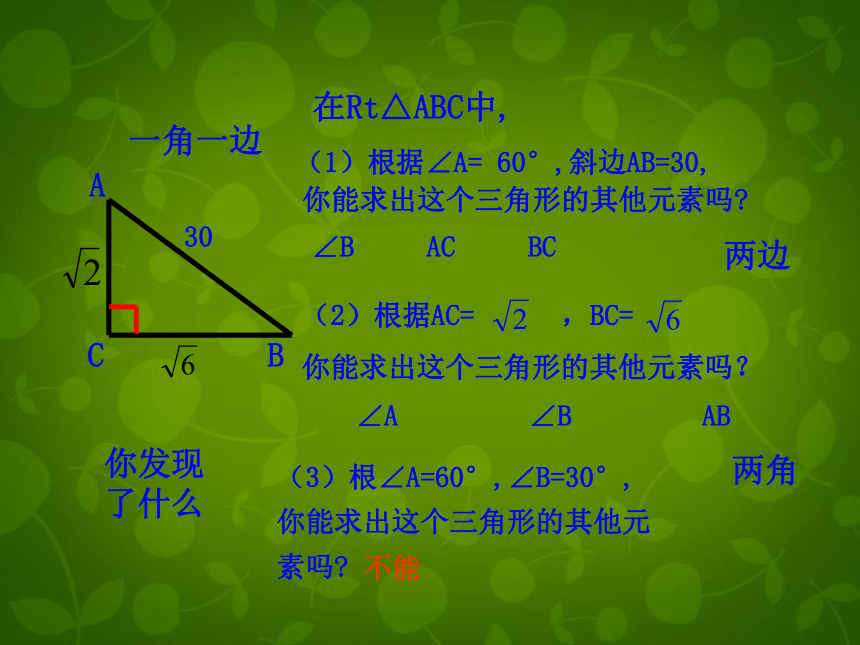
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
你能求出这个三角形的其他元素吗?
30
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由除直角外的已知元素求其余未知元素的过程,叫做解直角三角形.
定义:
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
【例1】如图,在Rt△ABC中,∠C=90°,
解这个直角三角形.
A
B
C
【例题】
【例2】如图,在Rt△ABC中, ∠C=90°,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位)
A
B
C
a
b=
c
20
35°
你还有其他方法求出c吗?
(江西·中考)如图,从点C测得树的顶角为33?,BC=20米,则树高AB= 米(用计算器计算,结果精确到0.1米).
【答案】13.0
AB=BC·tanC=20×tan33°≈13.0(米).
【跟踪训练】
1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
A
B
C
m
2.(东营·中考)如图,小明为了测
量其所在位置A点到河对岸B点之间
的距离,沿着与AB垂直的方向走了m
米,到达点C,测得∠ACB=α,那么
AB等于( )
A. m·sinα米 B. m·tanα米
C. m·cosα米 D. 米
B
3. (滨州·中考)边长为6cm的等边三角形中,其一边上高的长度为________cm.
【解析】一边上的高=6×sin60°=
【答案】
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.
忍耐之草是苦的,但最终会结出甘甜而柔软的果实.
——辛姆洛克
28.2 解直角三角形及其应用
28.2.1 解直角三角形
1.使学生理解直角三角形中六个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
2.渗透数形结合的数学思想,培养学生良好的学习习惯.
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____.
(2)锐角之间的关系:∠A+∠B=_____.
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
利用计算器可得 .
根据以上条件可以求出塔身中心线与垂直中
心线的夹角.你愿意试着计算一下吗?
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过点B向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
A
B
C
将上述问题推广到一般情形,就是:已知直角
三角形的斜边和一条直角边,求它的锐角的度数.
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
你能求出这个三角形的其他元素吗?
30
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由除直角外的已知元素求其余未知元素的过程,叫做解直角三角形.
定义:
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
【例1】如图,在Rt△ABC中,∠C=90°,
解这个直角三角形.
A
B
C
【例题】
【例2】如图,在Rt△ABC中, ∠C=90°,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位)
A
B
C
a
b=
c
20
35°
你还有其他方法求出c吗?
(江西·中考)如图,从点C测得树的顶角为33?,BC=20米,则树高AB= 米(用计算器计算,结果精确到0.1米).
【答案】13.0
AB=BC·tanC=20×tan33°≈13.0(米).
【跟踪训练】
1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
A
B
C
m
2.(东营·中考)如图,小明为了测
量其所在位置A点到河对岸B点之间
的距离,沿着与AB垂直的方向走了m
米,到达点C,测得∠ACB=α,那么
AB等于( )
A. m·sinα米 B. m·tanα米
C. m·cosα米 D. 米
B
3. (滨州·中考)边长为6cm的等边三角形中,其一边上高的长度为________cm.
【解析】一边上的高=6×sin60°=
【答案】
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.
忍耐之草是苦的,但最终会结出甘甜而柔软的果实.
——辛姆洛克
28.2 解直角三角形及其应用
28.2.1 解直角三角形
1.使学生理解直角三角形中六个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
2.渗透数形结合的数学思想,培养学生良好的学习习惯.
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____.
(2)锐角之间的关系:∠A+∠B=_____.
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
利用计算器可得 .
根据以上条件可以求出塔身中心线与垂直中
心线的夹角.你愿意试着计算一下吗?
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过点B向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
A
B
C
将上述问题推广到一般情形,就是:已知直角
三角形的斜边和一条直角边,求它的锐角的度数.
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
你能求出这个三角形的其他元素吗?
30
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由除直角外的已知元素求其余未知元素的过程,叫做解直角三角形.
定义:
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
【例1】如图,在Rt△ABC中,∠C=90°,
解这个直角三角形.
A
B
C
【例题】
【例2】如图,在Rt△ABC中, ∠C=90°,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位)
A
B
C
a
b=
c
20
35°
你还有其他方法求出c吗?
(江西·中考)如图,从点C测得树的顶角为33?,BC=20米,则树高AB= 米(用计算器计算,结果精确到0.1米).
【答案】13.0
AB=BC·tanC=20×tan33°≈13.0(米).
【跟踪训练】
1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
A
B
C
m
2.(东营·中考)如图,小明为了测
量其所在位置A点到河对岸B点之间
的距离,沿着与AB垂直的方向走了m
米,到达点C,测得∠ACB=α,那么
AB等于( )
A. m·sinα米 B. m·tanα米
C. m·cosα米 D. 米
B
3. (滨州·中考)边长为6cm的等边三角形中,其一边上高的长度为________cm.
【解析】一边上的高=6×sin60°=
【答案】
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.
忍耐之草是苦的,但最终会结出甘甜而柔软的果实.
——辛姆洛克
28.2.1 解直角三角形
1.使学生理解直角三角形中六个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
2.渗透数形结合的数学思想,培养学生良好的学习习惯.
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____.
(2)锐角之间的关系:∠A+∠B=_____.
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
利用计算器可得 .
根据以上条件可以求出塔身中心线与垂直中
心线的夹角.你愿意试着计算一下吗?
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过点B向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
A
B
C
将上述问题推广到一般情形,就是:已知直角
三角形的斜边和一条直角边,求它的锐角的度数.
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
你能求出这个三角形的其他元素吗?
30
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由除直角外的已知元素求其余未知元素的过程,叫做解直角三角形.
定义:
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
【例1】如图,在Rt△ABC中,∠C=90°,
解这个直角三角形.
A
B
C
【例题】
【例2】如图,在Rt△ABC中, ∠C=90°,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位)
A
B
C
a
b=
c
20
35°
你还有其他方法求出c吗?
(江西·中考)如图,从点C测得树的顶角为33?,BC=20米,则树高AB= 米(用计算器计算,结果精确到0.1米).
【答案】13.0
AB=BC·tanC=20×tan33°≈13.0(米).
【跟踪训练】
1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
A
B
C
m
2.(东营·中考)如图,小明为了测
量其所在位置A点到河对岸B点之间
的距离,沿着与AB垂直的方向走了m
米,到达点C,测得∠ACB=α,那么
AB等于( )
A. m·sinα米 B. m·tanα米
C. m·cosα米 D. 米
B
3. (滨州·中考)边长为6cm的等边三角形中,其一边上高的长度为________cm.
【解析】一边上的高=6×sin60°=
【答案】
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.
忍耐之草是苦的,但最终会结出甘甜而柔软的果实.
——辛姆洛克
28.2 解直角三角形及其应用
28.2.1 解直角三角形
1.使学生理解直角三角形中六个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
2.渗透数形结合的数学思想,培养学生良好的学习习惯.
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____.
(2)锐角之间的关系:∠A+∠B=_____.
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
利用计算器可得 .
根据以上条件可以求出塔身中心线与垂直中
心线的夹角.你愿意试着计算一下吗?
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过点B向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
A
B
C
将上述问题推广到一般情形,就是:已知直角
三角形的斜边和一条直角边,求它的锐角的度数.
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
你能求出这个三角形的其他元素吗?
30
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由除直角外的已知元素求其余未知元素的过程,叫做解直角三角形.
定义:
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
【例1】如图,在Rt△ABC中,∠C=90°,
解这个直角三角形.
A
B
C
【例题】
【例2】如图,在Rt△ABC中, ∠C=90°,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位)
A
B
C
a
b=
c
20
35°
你还有其他方法求出c吗?
(江西·中考)如图,从点C测得树的顶角为33?,BC=20米,则树高AB= 米(用计算器计算,结果精确到0.1米).
【答案】13.0
AB=BC·tanC=20×tan33°≈13.0(米).
【跟踪训练】
1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
A
B
C
m
2.(东营·中考)如图,小明为了测
量其所在位置A点到河对岸B点之间
的距离,沿着与AB垂直的方向走了m
米,到达点C,测得∠ACB=α,那么
AB等于( )
A. m·sinα米 B. m·tanα米
C. m·cosα米 D. 米
B
3. (滨州·中考)边长为6cm的等边三角形中,其一边上高的长度为________cm.
【解析】一边上的高=6×sin60°=
【答案】
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.
忍耐之草是苦的,但最终会结出甘甜而柔软的果实.
——辛姆洛克
28.2 解直角三角形及其应用
28.2.1 解直角三角形
1.使学生理解直角三角形中六个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
2.渗透数形结合的数学思想,培养学生良好的学习习惯.
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____.
(2)锐角之间的关系:∠A+∠B=_____.
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
利用计算器可得 .
根据以上条件可以求出塔身中心线与垂直中
心线的夹角.你愿意试着计算一下吗?
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过点B向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
A
B
C
将上述问题推广到一般情形,就是:已知直角
三角形的斜边和一条直角边,求它的锐角的度数.
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
你能求出这个三角形的其他元素吗?
30
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由除直角外的已知元素求其余未知元素的过程,叫做解直角三角形.
定义:
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
(勾股定理)
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
【例1】如图,在Rt△ABC中,∠C=90°,
解这个直角三角形.
A
B
C
【例题】
【例2】如图,在Rt△ABC中, ∠C=90°,∠B=35°,b=20,解这个直角三角形(结果保留小数点后一位)
A
B
C
a
b=
c
20
35°
你还有其他方法求出c吗?
(江西·中考)如图,从点C测得树的顶角为33?,BC=20米,则树高AB= 米(用计算器计算,结果精确到0.1米).
【答案】13.0
AB=BC·tanC=20×tan33°≈13.0(米).
【跟踪训练】
1.在下列直角三角形中不能求解的是( )
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
A
B
C
m
2.(东营·中考)如图,小明为了测
量其所在位置A点到河对岸B点之间
的距离,沿着与AB垂直的方向走了m
米,到达点C,测得∠ACB=α,那么
AB等于( )
A. m·sinα米 B. m·tanα米
C. m·cosα米 D. 米
B
3. (滨州·中考)边长为6cm的等边三角形中,其一边上高的长度为________cm.
【解析】一边上的高=6×sin60°=
【答案】
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用.
忍耐之草是苦的,但最终会结出甘甜而柔软的果实.
——辛姆洛克
