9.2.2 一元一次不等式的解法(第二课时) 课件 (共26张PPT)
文档属性
| 名称 | 9.2.2 一元一次不等式的解法(第二课时) 课件 (共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 08:45:36 | ||
图片预览








文档简介
泮水中学七年级数学课件
9.2.2 一元一次不等式
(第2课时)
门票70元,团体优惠
欢迎
光临
海龙屯
我们一起去旅游吧!
两名老师全额付款,其余的五五折(按报价的55%)
所有的人六折收费
(按报价的60%)
甲经理
乙经理
选择哪个提议更实惠?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题1 你是如何理解题意的呢?
问题探究
问题探究
问题2 如果购物款为x元,你能分别表示出在两家商场花费的钱数吗?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题探究
问题3 你能清楚直观地表示上述问题吗?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
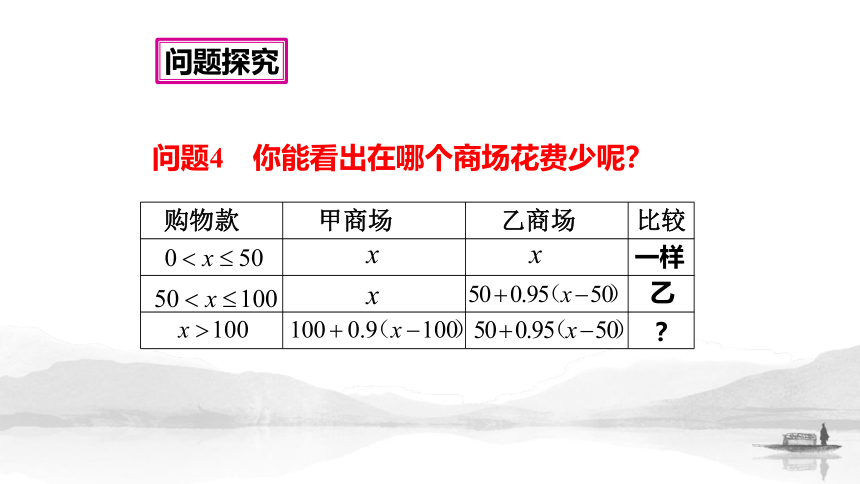
问题4 你能看出在哪个商场花费少呢?
购物款
甲商场
乙商场
比较
一样
乙
?
问题探究
问题5 如果累计购物超过100元,在哪家商场花费少呢?
分析:三种情况进行讨论
(1)什么情况下,到甲商场购物花费少?
(2) 什么情况下,到乙商场购物花费少?
(3)什么情况下,两商场花费一样?
问题探究
(1)若在甲超市花费少,则
.
得 .
问题探究
(2)若在乙超市花费少,则
.
得 .
问题探究
(3)若在两超市花费一样,则
.
得 .
问题探究
问题6 你能综合上面分析给出一个合理化的消费方案吗?
答:购物不超过50元和刚好是150元时,
在两家商场购物没有区别;超过50元而不到150元时在乙商场购物花费少;超过150元后,在甲商场购物花费少.
问题探究
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
问题1 你是如何理解题意的呢?
问题探究
问题2 此实际问题中的不等关系是什么?
问题探究
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
不等关系是:
问题探究
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
问题3 设x表示明年增加的空气质量良好
的天数,则明年空气质量是良好的天数是
多少?
问题探究
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
设x表示明年增加的空气质量良好的
天数,则明年空气质量是良好的天数
是:
问题探究
问题探究
问题4 你能列出不等式并解出来吗?
解:设明年比去年空气质量良好的天数增加了x天.
问题5 你能给出一个合理化的答案吗?
答:明年要比去年空气质量良好的天数
至少增加37,才能使这一年空气质量良
好的天数超过全年天数的70%.
问题探究
巩固练习
1.某工程队计划在10天内修路6 km.施工前2天修完1.2 km后,计划发生变化, 准备提前2天完成修路任务,以后几天 内平均每天至少要修路多少?
解:设以后几天平均每天至少要修路x米.
巩固练习
答:以后几天平均每天至少要修路 0.8米.
2.某次知识竞赛共有20道题,每一道题 答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题?
巩固练习
解:设至少要答对 道题.
巩固练习
答:至少要答对13道题.
门票70元,团体优惠
两名老师全额付款,其余的五五折(按报价的55%)
甲经理
乙经理
所有的人六折收费
(按报价的60%)
解: 设学生有x人,选甲经理的建议,则费用为: 70×2+70×55 %x = 140+38.5x;选乙经理的建议,则费用为:(2+x)×70 ×60%=84+42x
1)当甲乙经理的建议的费用一样多
140+38.5x =84+42x时,x=16,即当学生人数是16时,选择甲乙经理的建议的费用一样多;
3)当乙经理的建议更实惠
140+38.5x >84+42x时,
x < 16,即学生人数小于16时,
选择乙经理的建议更实惠;
2)当甲经理的建议更实惠
140+38.5x <84+42x时,
x>16,即当学生人数大于16时
选择甲经理的建议更实惠;
1.利用不等式来解决实际问题的步骤是什么?
实际问题
设未知数,列不等式
数学问题
(一元一次不等式)
解
不
等
式
数学问题的解
(一元一次不等式的解集)
实际问题的解答
检验
数学建模
总结归纳
2.一元一次不等式的实际问题中最关键是哪一步?
3.不等式的实际问题与方程的实际问题有什么相同和不同之处?
总结归纳
感谢您的聆听
9.2.2 一元一次不等式
(第2课时)
门票70元,团体优惠
欢迎
光临
海龙屯
我们一起去旅游吧!
两名老师全额付款,其余的五五折(按报价的55%)
所有的人六折收费
(按报价的60%)
甲经理
乙经理
选择哪个提议更实惠?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题1 你是如何理解题意的呢?
问题探究
问题探究
问题2 如果购物款为x元,你能分别表示出在两家商场花费的钱数吗?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题探究
问题3 你能清楚直观地表示上述问题吗?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题4 你能看出在哪个商场花费少呢?
购物款
甲商场
乙商场
比较
一样
乙
?
问题探究
问题5 如果累计购物超过100元,在哪家商场花费少呢?
分析:三种情况进行讨论
(1)什么情况下,到甲商场购物花费少?
(2) 什么情况下,到乙商场购物花费少?
(3)什么情况下,两商场花费一样?
问题探究
(1)若在甲超市花费少,则
.
得 .
问题探究
(2)若在乙超市花费少,则
.
得 .
问题探究
(3)若在两超市花费一样,则
.
得 .
问题探究
问题6 你能综合上面分析给出一个合理化的消费方案吗?
答:购物不超过50元和刚好是150元时,
在两家商场购物没有区别;超过50元而不到150元时在乙商场购物花费少;超过150元后,在甲商场购物花费少.
问题探究
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
问题1 你是如何理解题意的呢?
问题探究
问题2 此实际问题中的不等关系是什么?
问题探究
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
不等关系是:
问题探究
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
问题3 设x表示明年增加的空气质量良好
的天数,则明年空气质量是良好的天数是
多少?
问题探究
例1 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
设x表示明年增加的空气质量良好的
天数,则明年空气质量是良好的天数
是:
问题探究
问题探究
问题4 你能列出不等式并解出来吗?
解:设明年比去年空气质量良好的天数增加了x天.
问题5 你能给出一个合理化的答案吗?
答:明年要比去年空气质量良好的天数
至少增加37,才能使这一年空气质量良
好的天数超过全年天数的70%.
问题探究
巩固练习
1.某工程队计划在10天内修路6 km.施工前2天修完1.2 km后,计划发生变化, 准备提前2天完成修路任务,以后几天 内平均每天至少要修路多少?
解:设以后几天平均每天至少要修路x米.
巩固练习
答:以后几天平均每天至少要修路 0.8米.
2.某次知识竞赛共有20道题,每一道题 答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题?
巩固练习
解:设至少要答对 道题.
巩固练习
答:至少要答对13道题.
门票70元,团体优惠
两名老师全额付款,其余的五五折(按报价的55%)
甲经理
乙经理
所有的人六折收费
(按报价的60%)
解: 设学生有x人,选甲经理的建议,则费用为: 70×2+70×55 %x = 140+38.5x;选乙经理的建议,则费用为:(2+x)×70 ×60%=84+42x
1)当甲乙经理的建议的费用一样多
140+38.5x =84+42x时,x=16,即当学生人数是16时,选择甲乙经理的建议的费用一样多;
3)当乙经理的建议更实惠
140+38.5x >84+42x时,
x < 16,即学生人数小于16时,
选择乙经理的建议更实惠;
2)当甲经理的建议更实惠
140+38.5x <84+42x时,
x>16,即当学生人数大于16时
选择甲经理的建议更实惠;
1.利用不等式来解决实际问题的步骤是什么?
实际问题
设未知数,列不等式
数学问题
(一元一次不等式)
解
不
等
式
数学问题的解
(一元一次不等式的解集)
实际问题的解答
检验
数学建模
总结归纳
2.一元一次不等式的实际问题中最关键是哪一步?
3.不等式的实际问题与方程的实际问题有什么相同和不同之处?
总结归纳
感谢您的聆听
