人教版七年级下册数学 第九章不等式与不等式组 复习课课件【22张PPT】
文档属性
| 名称 | 人教版七年级下册数学 第九章不等式与不等式组 复习课课件【22张PPT】 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:06:25 | ||
图片预览







文档简介
第九章 不等式与不等式组
复习课
学习导航
学习目标
知识结构
知识梳理
典型例题
当堂检测
课堂总结
一、学习目标
1.进一步理解不等式的概念及其基本性质;
2.掌握一元一次不等式和一元一次不等式组的概念与解法;(重点)
3.能运用一元一次不等式(组)解决相关的数学问题和简单的
实际问题.
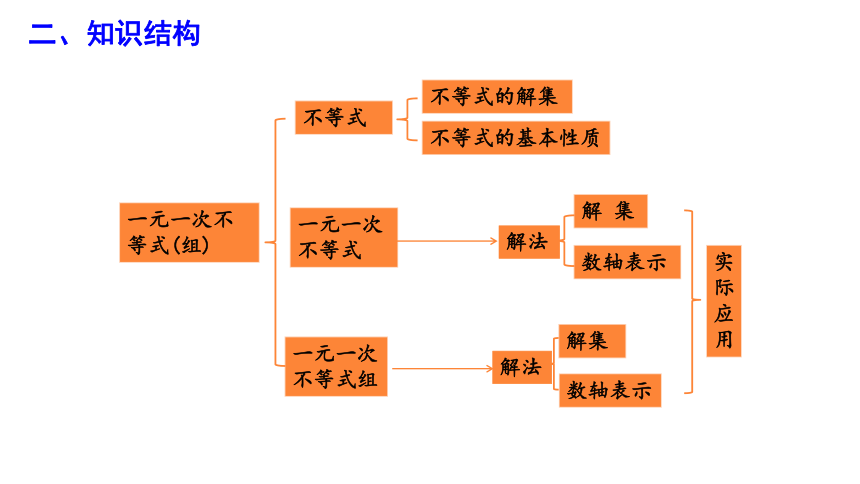
二、知识结构
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
三、知识梳理
(一)不等式的概念及性质
不等号有:>、≥、<、≤或≠.
用不等式号表示不等关系的式子叫做不等式.
性质1:如果a>b,那么a+c>b+c,且 a-c>b-c.
性质2:如果a>b,c>0,那么ac > bc , > .
性质3:如果a>b,c<0,那么ac < bc , < .
三、知识梳理
(二)一元一次不等式(组)的相关概念
1. 含有一个未知数,含未知数的项的次数是1、且不等号两边都是整式的不等式叫作一元一次不等式.
2. 使不等式成立的未知数的值叫做不等式的解;
3. 不等式的解集:这些解的全体称为这个不等式的解集;
4. 解不等式:求不等式解集的过程叫解不等式.
三、知识梳理
6. 这几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集.?
5. 几个含有同一个未知数的一元一次不等式组成的不等式组叫做一元一次不等式组.
三、知识梳理
(三)解一元一次不等式(组)
注意:在利用不等式的基本性质3时,一定要改变不等号的方向.
解一元一次不等式的一般步骤:
⑤将未知数系数化为1.
④合并同类项;
③移项;
②去括号;
①去分母;
解一元一次不等式组的一般步骤:
③ 找出各不等式解集的公共部分.
② 在同一数轴上表示每个不等式的解集;
① 分别解每一个不等式;
三、知识梳理
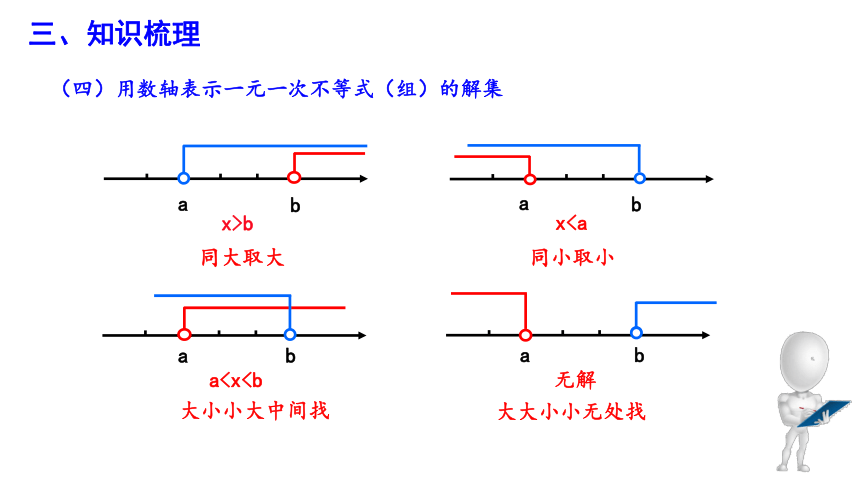
(四)用数轴表示一元一次不等式(组)的解集
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
a
b
a
b
a
b
a
b
三、知识梳理
(五)利用一元一次不等式(组)解决实际问题
1.根据题意,适当设出未知数;
2.找出题中能概括数量间关系的不等关系;
3.用未知数表示不等关系中的数量;
4.列出不等式(组)并求出其解集;
5.检验并根据实际问题的要求写出符合题意的解或解集,并写出答案.
四、典型例题
D
解析:根据不等式的基本性质3,不等式的两边同时乘(或除以)同一个负数,
不等号的方向改变,故D选项错误,应为-4a<-4b.
例1.若a>b,则下列结论错误的是( )
A.a-5>b-8 B.5+a>b+5
C. D.-4a>-4b
【当堂检测】
1. 已知a A.3a<3b B.-3a<-3b
C.a-3B
四、典型例题
例2. 解不等式 ,并把它的解集表示在数轴上.
解:
去分母,得 2(4+x)-6<3x.
去括号,得 8+2x-6<3x.
移项、合并同类项,得 -x<-2.
x的系数化为1,得 x>2.
这个不等式的解集在数轴上表示如下:
2
1
0
3
4
四、典型例题
归纳总结:先求出不等式的解集,然后根据“大于向右画,小于向左画,
含等号用实心圆点,不含等号用空心圆圈”的原则在数轴上表示解集.
解一元一次不等式的几点注意:
(3)系数化为1时,若系数为负数,要改变不等号的方向.
(2)移项要变号;
(1)去分母时不要漏乘常数项;
四、典型例题
例3.解不等式组 ,利用数轴确定不等式组的解集.
解:
解不等式5x+1>3(x+1),得x>1,
解不等式x-3≤7-x,得x≤5,
所以不等式组的解集为1<x≤5.
两个不等式的解集表示在数轴上如下:
0
4
1
2
3
5
【当堂检测】
2. 解不等式 ,并把它的解集表示在数轴上.
y≤
0
解:
去分母,得 2(y+1)-3(2y-5)≥12.
去括号,得 2y+2-6y+15≥12.
移项、合并同类项,得 -4y≥-5.
x的系数化为1,得
这个不等式的解集在数轴上表示如下:
【当堂检测】
3. x取哪些整数值时,不等式x-1≥2与3x-7<8同时成立?
解:联立可得
①
②
由①得:x≥3 ;
由②得:x<5;
在数轴表示:
不等式组的解集是3≤x<5.
所以x可取的整数值是3、4.
0
4
1
2
3
5
四、典型例题
例4.某小区计划购进甲、乙两种树苗,已知甲、乙两种树苗每株分别为8元、
6元.若购买甲、乙两种树苗共360株,并且甲树苗的数量不少于乙树苗的一半,请你设计一种费用最少的购买方案.
解:设购买甲树苗的数量为x株,依题意,得
解得x≥120.
因为甲树苗比乙树苗每株多2元,
所以要节省费用,则要尽量少买甲树苗.
又因为x最小为120,
所以购买甲树苗120株,乙树苗240株,此时费用最省.
四、典型例题
归纳总结:解不等式的应用问题的步骤包括审、设、列、解、找、答这几个
环节,而在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),
然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问
题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.
【当堂检测】
4.小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时追上或超过小明,速度至少应是多少?
解:
设小亮的速度为x千米/时,
解得x≥16.
列不等式,得
答:小亮的速度至少为16千米/时.
40分= 小时
【当堂检测】
5.一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分
4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5因为x是整数,所以x=6,7,8.
答:小朋友有6人,玩具有22件;有7人,玩具有25件;有8人,玩具有28件.
五、课堂总结
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
复习课
学习导航
学习目标
知识结构
知识梳理
典型例题
当堂检测
课堂总结
一、学习目标
1.进一步理解不等式的概念及其基本性质;
2.掌握一元一次不等式和一元一次不等式组的概念与解法;(重点)
3.能运用一元一次不等式(组)解决相关的数学问题和简单的
实际问题.
二、知识结构
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
三、知识梳理
(一)不等式的概念及性质
不等号有:>、≥、<、≤或≠.
用不等式号表示不等关系的式子叫做不等式.
性质1:如果a>b,那么a+c>b+c,且 a-c>b-c.
性质2:如果a>b,c>0,那么ac > bc , > .
性质3:如果a>b,c<0,那么ac < bc , < .
三、知识梳理
(二)一元一次不等式(组)的相关概念
1. 含有一个未知数,含未知数的项的次数是1、且不等号两边都是整式的不等式叫作一元一次不等式.
2. 使不等式成立的未知数的值叫做不等式的解;
3. 不等式的解集:这些解的全体称为这个不等式的解集;
4. 解不等式:求不等式解集的过程叫解不等式.
三、知识梳理
6. 这几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集.?
5. 几个含有同一个未知数的一元一次不等式组成的不等式组叫做一元一次不等式组.
三、知识梳理
(三)解一元一次不等式(组)
注意:在利用不等式的基本性质3时,一定要改变不等号的方向.
解一元一次不等式的一般步骤:
⑤将未知数系数化为1.
④合并同类项;
③移项;
②去括号;
①去分母;
解一元一次不等式组的一般步骤:
③ 找出各不等式解集的公共部分.
② 在同一数轴上表示每个不等式的解集;
① 分别解每一个不等式;
三、知识梳理
(四)用数轴表示一元一次不等式(组)的解集
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa
a
b
a
b
a
b
a
b
三、知识梳理
(五)利用一元一次不等式(组)解决实际问题
1.根据题意,适当设出未知数;
2.找出题中能概括数量间关系的不等关系;
3.用未知数表示不等关系中的数量;
4.列出不等式(组)并求出其解集;
5.检验并根据实际问题的要求写出符合题意的解或解集,并写出答案.
四、典型例题
D
解析:根据不等式的基本性质3,不等式的两边同时乘(或除以)同一个负数,
不等号的方向改变,故D选项错误,应为-4a<-4b.
例1.若a>b,则下列结论错误的是( )
A.a-5>b-8 B.5+a>b+5
C. D.-4a>-4b
【当堂检测】
1. 已知a
C.a-3
四、典型例题
例2. 解不等式 ,并把它的解集表示在数轴上.
解:
去分母,得 2(4+x)-6<3x.
去括号,得 8+2x-6<3x.
移项、合并同类项,得 -x<-2.
x的系数化为1,得 x>2.
这个不等式的解集在数轴上表示如下:
2
1
0
3
4
四、典型例题
归纳总结:先求出不等式的解集,然后根据“大于向右画,小于向左画,
含等号用实心圆点,不含等号用空心圆圈”的原则在数轴上表示解集.
解一元一次不等式的几点注意:
(3)系数化为1时,若系数为负数,要改变不等号的方向.
(2)移项要变号;
(1)去分母时不要漏乘常数项;
四、典型例题
例3.解不等式组 ,利用数轴确定不等式组的解集.
解:
解不等式5x+1>3(x+1),得x>1,
解不等式x-3≤7-x,得x≤5,
所以不等式组的解集为1<x≤5.
两个不等式的解集表示在数轴上如下:
0
4
1
2
3
5
【当堂检测】
2. 解不等式 ,并把它的解集表示在数轴上.
y≤
0
解:
去分母,得 2(y+1)-3(2y-5)≥12.
去括号,得 2y+2-6y+15≥12.
移项、合并同类项,得 -4y≥-5.
x的系数化为1,得
这个不等式的解集在数轴上表示如下:
【当堂检测】
3. x取哪些整数值时,不等式x-1≥2与3x-7<8同时成立?
解:联立可得
①
②
由①得:x≥3 ;
由②得:x<5;
在数轴表示:
不等式组的解集是3≤x<5.
所以x可取的整数值是3、4.
0
4
1
2
3
5
四、典型例题
例4.某小区计划购进甲、乙两种树苗,已知甲、乙两种树苗每株分别为8元、
6元.若购买甲、乙两种树苗共360株,并且甲树苗的数量不少于乙树苗的一半,请你设计一种费用最少的购买方案.
解:设购买甲树苗的数量为x株,依题意,得
解得x≥120.
因为甲树苗比乙树苗每株多2元,
所以要节省费用,则要尽量少买甲树苗.
又因为x最小为120,
所以购买甲树苗120株,乙树苗240株,此时费用最省.
四、典型例题
归纳总结:解不等式的应用问题的步骤包括审、设、列、解、找、答这几个
环节,而在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),
然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问
题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.
【当堂检测】
4.小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时追上或超过小明,速度至少应是多少?
解:
设小亮的速度为x千米/时,
解得x≥16.
列不等式,得
答:小亮的速度至少为16千米/时.
40分= 小时
【当堂检测】
5.一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分
4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5
答:小朋友有6人,玩具有22件;有7人,玩具有25件;有8人,玩具有28件.
五、课堂总结
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
