人教版七年级下数学课件9.3 一元一次不等式组(27张PPT)
文档属性
| 名称 | 人教版七年级下数学课件9.3 一元一次不等式组(27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 932.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:10:35 | ||
图片预览







文档简介
问题 用每分可抽30 t 水的抽水机来抽污水管道里寄存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?
1
一元一次不等式组的概念及解集
设用x min将污水抽完,则x同时满足不等式
30x>1200,
30x<1500.
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组,记作
30x>1200,
30x<1500.
30x>1200 和30x<1500
像 这样,关于同一未知数的两个
一元一次不等式合在一起,就组成一个一元一次不等式组.
30x>1200,
30x<1500.
判断下列不等式组是否为一元一次不等式组:
×
×
√
√
思考 怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳 我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
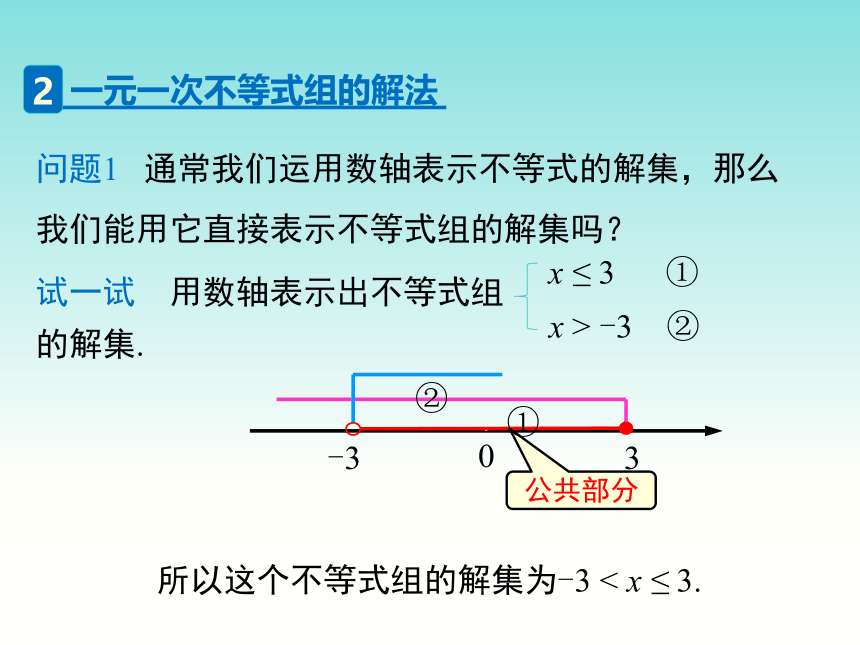
问题1 通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试 用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
2
一元一次不等式组的解法
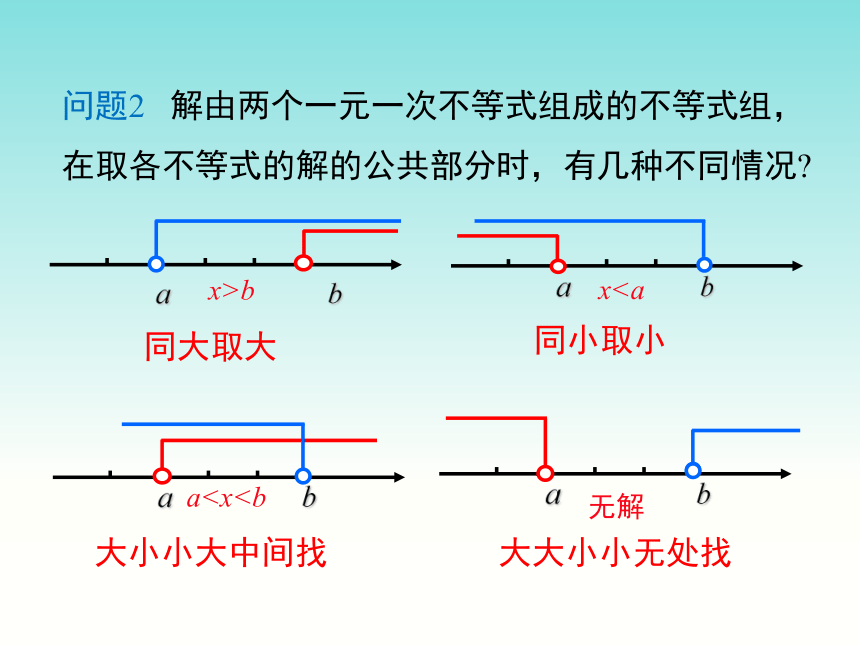
问题2 解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
填表:
不等式组
不等式组的解集
x﹥-3
-5﹤x≤-3
x<-3
无解
试一试 解上面问题中的不等式组
解:解不等式①,得
解不等式②,得
x>40.
x<50.
30x>1200,
30x<1500.
①
②
0
40
50
把不等式①和②的解集在数轴上表示出来.
从上图容易看出,x的取值范围是40<x <50.
这就是说,将污水抽完所用时间多余40 min而少于50 min.
解不等式②,得
x <-3.
解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
例1
解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,
如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例2
解不等式组:
解: 解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.所以,这个不等式组无解.
0
-2
3
例3
已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3+2b= -1
解得 a=1 , b= - 2
所以(a+1)(b-1)=2×(-3)=-6
例4
3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
3
一元一次不等式组的应用
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
例5
1.选择下列不等式组的正确解集.
①
x ≥ -1
x≥ 2
x≥ 2
x ≥ -1
-1≤ x≤ 2
无解
A
C
D
B
②
x< -1
x< 2
x< 2
x< -1
-1< x< 2
无解
B
D
C
A
A
无解
③
x ≥ -1
x ≥ -1
x< 2
x< 2
-1≤ x< 2
B
D
A
C
C
无解
x< -1
x< -1
④
x≥ 2
x≥ 2
-1< x≥ 2
C
B
A
D
D
B
解不等式②,得
x <6.
2. 解不等式组:
解: 解不等式①,得
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
3
0
6
因此,原不等式组的解集为
解不等式②,得
x >4.
3. 解不等式组:
解: 解不等式①,得
x >2.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
2
0
4
由图可知,不等式①、②的解集的公共部分就是x >4,所以这个不等式组的解集是x >4.
4. x取哪些整数值时,不等式
2-x≥0
与
都成立?
解:由题意可得不等式组
解不等式①,得x≤2,
解不等式②,得x>-3.
故此不等式组的解集为-3<x≤2,x可取的整数
值为-2,-1,0,1,2.
①
②
5.把一篮苹果分给几个学生,若每人分4个,则剩余
3个;若每人分6个,则最后一个学生最多分2个,
求学生人数和苹果分别是多少?
解:设学生有x个,则苹果有(4x+3)个,根据题意,得
(4x+3)-6(x-1)>0,
(4x+3)-6(x-1)≤2.
解不等式组,得3.5≤x<4.5
根据题意,x的值应是整数,所以x=4,则4x+3=19.
答:学生有4人,苹果有19个.
6.某校今年冬季烧煤取暖时间为4个月.如果每月比计划
多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比
计划少烧5吨煤,那么取暖用煤总量不足68吨.若设该校
计划每月烧煤 x t,求x的取值范围.
4(x+5)>100, ①
4(x-5)<68. ②
解不等式②,得
x <22.
解不等式①,得
x >20.
因此,原不等式组的解集为 20<x <22.
解:根据题意,得
解:①×2+②得:5x=10m-5,得:x=2m-1.
①-②×2得:5y=5m+40,得:y=m+8.
又∵x,y的值都是正数,且x∴
解得∴m的取值范围为 <m<9.
2m-1>0
m+8>0
2m-17.已知方程组 的解x,y的值都
是正数,且x2x+y=5m+6 ①
x-2y=-17 ②
一元一次不等式组
一元一次不等式组的概念
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
↓
一元一次不等式组的解集在数轴上的表示
一元一次不等式组的解集
解一元一次不等式组
→
↓
1
一元一次不等式组的概念及解集
设用x min将污水抽完,则x同时满足不等式
30x>1200,
30x<1500.
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组,记作
30x>1200,
30x<1500.
30x>1200 和30x<1500
像 这样,关于同一未知数的两个
一元一次不等式合在一起,就组成一个一元一次不等式组.
30x>1200,
30x<1500.
判断下列不等式组是否为一元一次不等式组:
×
×
√
√
思考 怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳 我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
问题1 通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试 用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
2
一元一次不等式组的解法
问题2 解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa
填表:
不等式组
不等式组的解集
x﹥-3
-5﹤x≤-3
x<-3
无解
试一试 解上面问题中的不等式组
解:解不等式①,得
解不等式②,得
x>40.
x<50.
30x>1200,
30x<1500.
①
②
0
40
50
把不等式①和②的解集在数轴上表示出来.
从上图容易看出,x的取值范围是40<x <50.
这就是说,将污水抽完所用时间多余40 min而少于50 min.
解不等式②,得
x <-3.
解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
例1
解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,
如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例2
解不等式组:
解: 解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.所以,这个不等式组无解.
0
-2
3
例3
已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3+2b= -1
解得 a=1 , b= - 2
所以(a+1)(b-1)=2×(-3)=-6
例4
3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
3
一元一次不等式组的应用
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
例5
1.选择下列不等式组的正确解集.
①
x ≥ -1
x≥ 2
x≥ 2
x ≥ -1
-1≤ x≤ 2
无解
A
C
D
B
②
x< -1
x< 2
x< 2
x< -1
-1< x< 2
无解
B
D
C
A
A
无解
③
x ≥ -1
x ≥ -1
x< 2
x< 2
-1≤ x< 2
B
D
A
C
C
无解
x< -1
x< -1
④
x≥ 2
x≥ 2
-1< x≥ 2
C
B
A
D
D
B
解不等式②,得
x <6.
2. 解不等式组:
解: 解不等式①,得
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
3
0
6
因此,原不等式组的解集为
解不等式②,得
x >4.
3. 解不等式组:
解: 解不等式①,得
x >2.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
2
0
4
由图可知,不等式①、②的解集的公共部分就是x >4,所以这个不等式组的解集是x >4.
4. x取哪些整数值时,不等式
2-x≥0
与
都成立?
解:由题意可得不等式组
解不等式①,得x≤2,
解不等式②,得x>-3.
故此不等式组的解集为-3<x≤2,x可取的整数
值为-2,-1,0,1,2.
①
②
5.把一篮苹果分给几个学生,若每人分4个,则剩余
3个;若每人分6个,则最后一个学生最多分2个,
求学生人数和苹果分别是多少?
解:设学生有x个,则苹果有(4x+3)个,根据题意,得
(4x+3)-6(x-1)>0,
(4x+3)-6(x-1)≤2.
解不等式组,得3.5≤x<4.5
根据题意,x的值应是整数,所以x=4,则4x+3=19.
答:学生有4人,苹果有19个.
6.某校今年冬季烧煤取暖时间为4个月.如果每月比计划
多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比
计划少烧5吨煤,那么取暖用煤总量不足68吨.若设该校
计划每月烧煤 x t,求x的取值范围.
4(x+5)>100, ①
4(x-5)<68. ②
解不等式②,得
x <22.
解不等式①,得
x >20.
因此,原不等式组的解集为 20<x <22.
解:根据题意,得
解:①×2+②得:5x=10m-5,得:x=2m-1.
①-②×2得:5y=5m+40,得:y=m+8.
又∵x,y的值都是正数,且x
解得
2m-1>0
m+8>0
2m-1
是正数,且x
x-2y=-17 ②
一元一次不等式组
一元一次不等式组的概念
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
↓
一元一次不等式组的解集在数轴上的表示
一元一次不等式组的解集
解一元一次不等式组
→
↓
