人教版数学七年级下册 9.2-一元一次不等式课件(共25张ppt)
文档属性
| 名称 | 人教版数学七年级下册 9.2-一元一次不等式课件(共25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 226.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 23:59:00 | ||
图片预览






文档简介
9.2 一元一次不等式
知识回顾
1.不等式的性质是什么?
性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c>b±c
性质2 :不等式两边乘(或除以)同一个正数,不等号的方向不变.
性质3 :不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a>b,c>0,那么ac>bc (或 )
如果a>b,c<0,那么ac<bc (或 )
知识回顾
下列一元一次方程:
x-7=26, 3x=2x+1, x=50 , -4x=3.
它们有哪些共同特征?
① 未知数个数:1个
② 未知数次数:1次
含有一个未知数,并且未知数的次数是1的方程,叫做一元一次方程.
2.什么是一元一次方程?
探究1
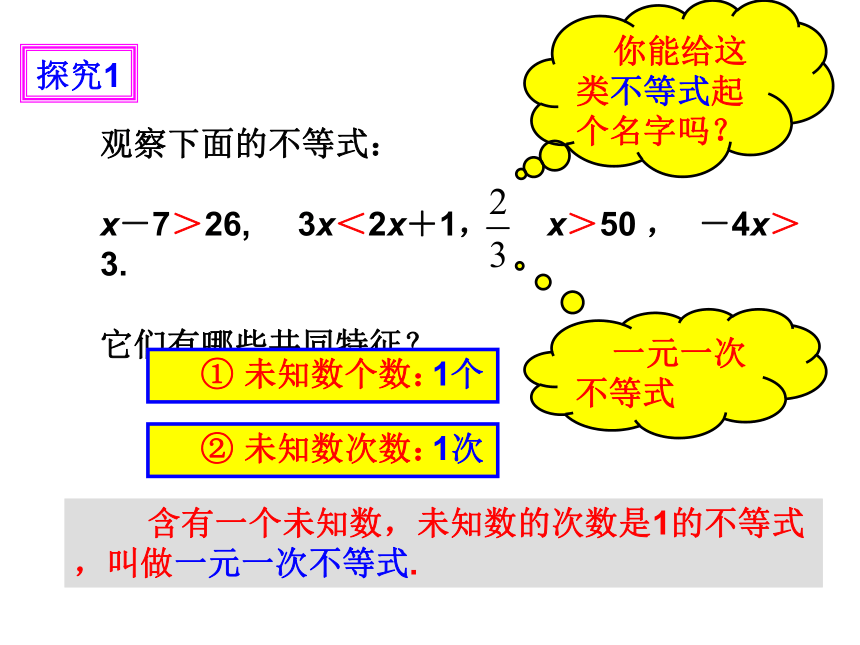
观察下面的不等式:
x-7>26, 3x<2x+1, x>50 , -4x>3.
它们有哪些共同特征?
① 未知数个数:
② 未知数次数:
含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
1个
1次
你能给这类不等式起个名字吗?
一元一次不等式
练习1
下列不等式中,哪些是一元一次不等式?
③-2x<5;
①3+5>7;
②x-y≤2;
④
⑦2x-3>1;
⑥3m-2<n+7;
⑤x2+3<2;
⑧3-2a≥5.
不是
不是
是
不是
不是
不是
是
是
探究2
x-7+7>26+7
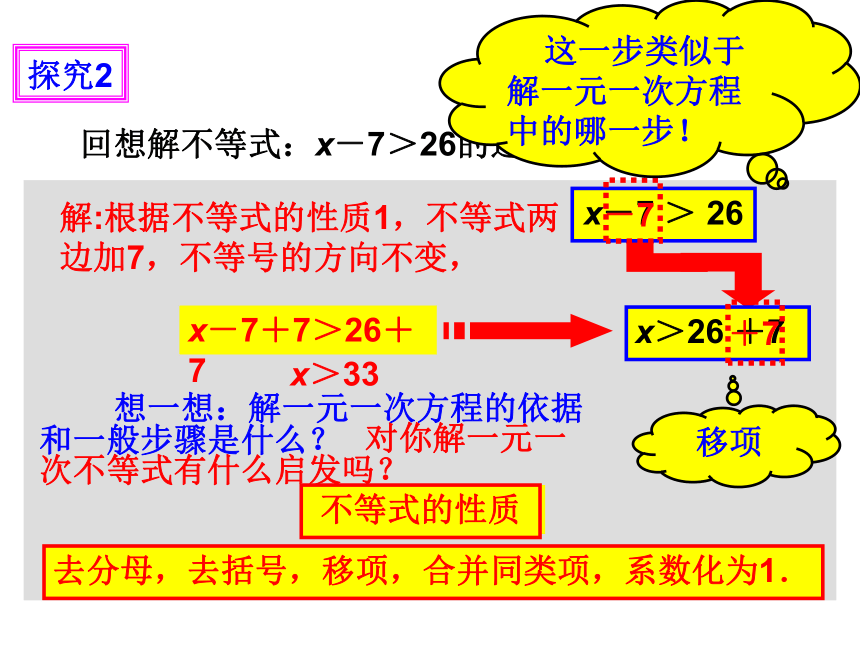
回想解不等式:x-7>26的过程:
解:根据不等式的性质1,不等式两边加7,不等号的方向不变,
x>33
x>26 +7
x-7 > 26
x-7+7>26+7
-7
+7
这一步类似于解一元一次方程中的哪一步!
移项
想一想:解一元一次方程的依据和一般步骤是什么?
等式的性质
去分母,去括号,移项,合并同类项,系数化为1.
不等式的性质
对你解一元一次不等式有什么启发吗?
去分母,去括号,移项,合并同类项,系数化为1.
例1
解下列不等式,并在数轴上表示解集:
系数化为1,得
(1)2(1+x)<3
(2)
解:(1)去括号,得 2+2x<3
移项,得 2x<3-2
合并同类项,得 2x<1
这个不等式的解集在数轴上表示为:
例1
解下列不等式,并在数轴上表示解集:
(1)2(1+x)<3
(2)
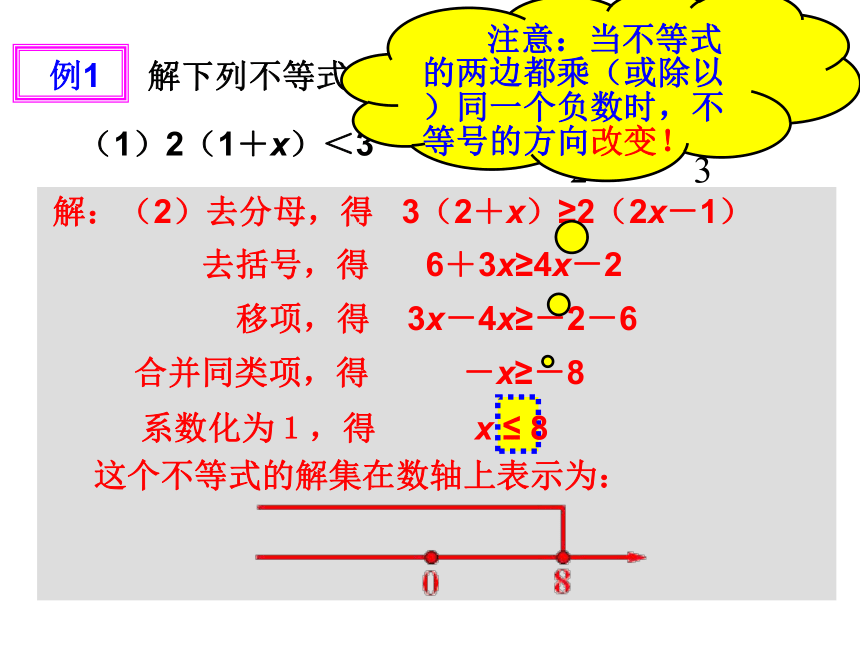
解:(2)去分母,得 3(2+x)≥2(2x-1)
移项,得 3x-4x≥-2-6
合并同类项,得 -x≥-8
这个不等式的解集在数轴上表示为:
去括号,得 6+3x≥4x-2
系数化为1,得 x ≤ 8
注意:当不等式的两边都乘(或除以)同一个负数时,不等号的方向改变!
归纳
说一说:解一元一次方程与一元一次不等式的相同与不同之处?
相同之处
基本步相同:去分母,去括号,移项,合并同类项,系数化为1.
基本思想相同:都是运用化归思想,将一元一次方程或一元一次不等式变形为最简形式.
不同之处
解法依据不同:解一元一次不等式的依据是不等式的性质,解一元一次方程的依据是等式的性质.
最简形式不同:一元一次不等式的最简形式是 x <a或x>a ,一元一次方程的最简形式是x=a.
练习2
解一元一次不等式 ,并把它的解集在数轴上表示出来.
解:去分母,得 2×x≤3×10+5×(x-10)
移项,得 2x-5x≤30-50
合并同类项,得 -3x≤-20
这个不等式的解集在数轴上表示为:
去括号,得 2x≤30+5x-50
系数化为1,得 x≥
应用提高
1.去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60﹪,如果明年(365天)这样的比值要超过70﹪,那么明年空气质量良好的天数要比去年至少增加多少?
题中未知量是谁?
明年比去年空气质量良好的天数增加的天数.
题中包含哪些不等关系是什么?
明年空气质量良好的天数
明年天数
>70%
应用提高
1.去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60﹪,如果明年(365天)这样的比值要超过70﹪,那么明年空气质量良好的天数要比去年至少增加多少?
解:设明年比去年空气质量良好的天数增加了x天.由题可列不等式:
答:明年要比去年空气质量良好的天数至少增加37,才能使这一年空气质量良好的天数超过全年天数的70%.
去分母,得
移项,合并同类项,得
由x应为正整数,得 x≥37
应用提高
2.甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:甲商场优惠方案的起点为购物款达______元后;乙商场优惠方案的起点为购物款达_____元后.分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元;
100
50
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
如果购物款为x元,你能分别表示出在两家商场花费的钱数吗?
购物款
甲商场
乙商场
比较
乙
一样
哪家花费少呢?
有三种情况!
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
①若到甲商场购物花费少,则
50+0.95(x-50)>100+0.9(x-100) .
解得 x>150 .
这就是说,累计购物超过150元时,到甲商场购物花费少.
当累计购物超过100元时,(即x>100时)
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
②若到乙商场购物花费少,则
50+0.95(x-50)<100+0.9(x-100) .
解得 x<150 .
这就是说,累计购物超过100元而不到150元时,到乙商场购物花费少.
当累计购物超过100元时,(即x>100时)
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
③若50+0.95(x-50)=100+0.9(x-100) .
解得 x=150 .
这就是说,累计购物为150元时,到甲、乙两商场购物花费一样.
当累计购物超过100元时,(即x>100时)
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
你能综合上面分析给出一个合理化的消费方案吗?
答:累计购物不超过50元和刚好是150元时,在甲、乙两家商场购物花费一样;
累计购物超过50元而不到150元时,到乙商场购物花费少;
累计购物超过150元时,到甲商场购物花费少.
归纳
数学问题
(一元一次不等式)
实际问题
设未知数
列不等式
解不等式
数学问题的解
(一元一次不等式的解集)
实际问题的答案
检验
利用不等式解决实际问题的基本思路:
数学建模
今天我们学习了哪些知识?
1.怎样解一元一次不等式?解一元一次不等式和解一元一次方程有哪些相同和不同之处?
2.利用不等式来解决实际问题的步骤是什么?
3.一元一次不等式的实际问题中最关键是哪一步?
体验收获
达标测评
1.解下列不等式,并在数轴上表示解集:
(1)5x+2>3(x-1)
解:(1)去括号得 5x+2>3x-3
移项得 5x-3x>-3-2
合并同类项得 2x>-5
系数化为1 得 x>-2.5
这个不等式的解集在数轴上表示为:
达标测评
1.解下列不等式,并在数轴上表示解集:
(1)5x+2>3(x-1)
解:(2)去分母得 x-2≤14- 3x
移项得 x+3x≤14+2
合并同类项得 4x≤16
系数化为1 得 x ≤4
这个不等式的解集在数轴上表示为:
达标测评
2.某工程队计划在10天内修路6 km.施工前2天修完1.2 km后,计划发生变化, 准备提前2天完成修路任务,以后几天内平均每天至少要修路多少?
解:设以后几天内平均每天至少要修路x千米.则
6x≥6-1.2
解得 x≥0.8
答:以后几天平均每天至少要修路 0.8千米.
达标测评
3.某公司要招甲、乙两种工作人员30人,甲种工作人员月薪600元,乙种工作人员月薪1000元.现要求每月总工资不能超过2.2万元,问至多可招乙种工作人员多少名?
解:设至多可招乙种工作人员x名,则甲种工作人员为(30-x)名,根据题意得:
600(30-x)+1000x≤22000
解得 x≤10
答:至多可招乙种工作人员10名.
知识回顾
1.不等式的性质是什么?
性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c>b±c
性质2 :不等式两边乘(或除以)同一个正数,不等号的方向不变.
性质3 :不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a>b,c>0,那么ac>bc (或 )
如果a>b,c<0,那么ac<bc (或 )
知识回顾
下列一元一次方程:
x-7=26, 3x=2x+1, x=50 , -4x=3.
它们有哪些共同特征?
① 未知数个数:1个
② 未知数次数:1次
含有一个未知数,并且未知数的次数是1的方程,叫做一元一次方程.
2.什么是一元一次方程?
探究1
观察下面的不等式:
x-7>26, 3x<2x+1, x>50 , -4x>3.
它们有哪些共同特征?
① 未知数个数:
② 未知数次数:
含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
1个
1次
你能给这类不等式起个名字吗?
一元一次不等式
练习1
下列不等式中,哪些是一元一次不等式?
③-2x<5;
①3+5>7;
②x-y≤2;
④
⑦2x-3>1;
⑥3m-2<n+7;
⑤x2+3<2;
⑧3-2a≥5.
不是
不是
是
不是
不是
不是
是
是
探究2
x-7+7>26+7
回想解不等式:x-7>26的过程:
解:根据不等式的性质1,不等式两边加7,不等号的方向不变,
x>33
x>26 +7
x-7 > 26
x-7+7>26+7
-7
+7
这一步类似于解一元一次方程中的哪一步!
移项
想一想:解一元一次方程的依据和一般步骤是什么?
等式的性质
去分母,去括号,移项,合并同类项,系数化为1.
不等式的性质
对你解一元一次不等式有什么启发吗?
去分母,去括号,移项,合并同类项,系数化为1.
例1
解下列不等式,并在数轴上表示解集:
系数化为1,得
(1)2(1+x)<3
(2)
解:(1)去括号,得 2+2x<3
移项,得 2x<3-2
合并同类项,得 2x<1
这个不等式的解集在数轴上表示为:
例1
解下列不等式,并在数轴上表示解集:
(1)2(1+x)<3
(2)
解:(2)去分母,得 3(2+x)≥2(2x-1)
移项,得 3x-4x≥-2-6
合并同类项,得 -x≥-8
这个不等式的解集在数轴上表示为:
去括号,得 6+3x≥4x-2
系数化为1,得 x ≤ 8
注意:当不等式的两边都乘(或除以)同一个负数时,不等号的方向改变!
归纳
说一说:解一元一次方程与一元一次不等式的相同与不同之处?
相同之处
基本步相同:去分母,去括号,移项,合并同类项,系数化为1.
基本思想相同:都是运用化归思想,将一元一次方程或一元一次不等式变形为最简形式.
不同之处
解法依据不同:解一元一次不等式的依据是不等式的性质,解一元一次方程的依据是等式的性质.
最简形式不同:一元一次不等式的最简形式是 x <a或x>a ,一元一次方程的最简形式是x=a.
练习2
解一元一次不等式 ,并把它的解集在数轴上表示出来.
解:去分母,得 2×x≤3×10+5×(x-10)
移项,得 2x-5x≤30-50
合并同类项,得 -3x≤-20
这个不等式的解集在数轴上表示为:
去括号,得 2x≤30+5x-50
系数化为1,得 x≥
应用提高
1.去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60﹪,如果明年(365天)这样的比值要超过70﹪,那么明年空气质量良好的天数要比去年至少增加多少?
题中未知量是谁?
明年比去年空气质量良好的天数增加的天数.
题中包含哪些不等关系是什么?
明年空气质量良好的天数
明年天数
>70%
应用提高
1.去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60﹪,如果明年(365天)这样的比值要超过70﹪,那么明年空气质量良好的天数要比去年至少增加多少?
解:设明年比去年空气质量良好的天数增加了x天.由题可列不等式:
答:明年要比去年空气质量良好的天数至少增加37,才能使这一年空气质量良好的天数超过全年天数的70%.
去分母,得
移项,合并同类项,得
由x应为正整数,得 x≥37
应用提高
2.甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:甲商场优惠方案的起点为购物款达______元后;乙商场优惠方案的起点为购物款达_____元后.分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元;
100
50
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
如果购物款为x元,你能分别表示出在两家商场花费的钱数吗?
购物款
甲商场
乙商场
比较
乙
一样
哪家花费少呢?
有三种情况!
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
①若到甲商场购物花费少,则
50+0.95(x-50)>100+0.9(x-100) .
解得 x>150 .
这就是说,累计购物超过150元时,到甲商场购物花费少.
当累计购物超过100元时,(即x>100时)
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
②若到乙商场购物花费少,则
50+0.95(x-50)<100+0.9(x-100) .
解得 x<150 .
这就是说,累计购物超过100元而不到150元时,到乙商场购物花费少.
当累计购物超过100元时,(即x>100时)
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
③若50+0.95(x-50)=100+0.9(x-100) .
解得 x=150 .
这就是说,累计购物为150元时,到甲、乙两商场购物花费一样.
当累计购物超过100元时,(即x>100时)
应用提高
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
你能综合上面分析给出一个合理化的消费方案吗?
答:累计购物不超过50元和刚好是150元时,在甲、乙两家商场购物花费一样;
累计购物超过50元而不到150元时,到乙商场购物花费少;
累计购物超过150元时,到甲商场购物花费少.
归纳
数学问题
(一元一次不等式)
实际问题
设未知数
列不等式
解不等式
数学问题的解
(一元一次不等式的解集)
实际问题的答案
检验
利用不等式解决实际问题的基本思路:
数学建模
今天我们学习了哪些知识?
1.怎样解一元一次不等式?解一元一次不等式和解一元一次方程有哪些相同和不同之处?
2.利用不等式来解决实际问题的步骤是什么?
3.一元一次不等式的实际问题中最关键是哪一步?
体验收获
达标测评
1.解下列不等式,并在数轴上表示解集:
(1)5x+2>3(x-1)
解:(1)去括号得 5x+2>3x-3
移项得 5x-3x>-3-2
合并同类项得 2x>-5
系数化为1 得 x>-2.5
这个不等式的解集在数轴上表示为:
达标测评
1.解下列不等式,并在数轴上表示解集:
(1)5x+2>3(x-1)
解:(2)去分母得 x-2≤14- 3x
移项得 x+3x≤14+2
合并同类项得 4x≤16
系数化为1 得 x ≤4
这个不等式的解集在数轴上表示为:
达标测评
2.某工程队计划在10天内修路6 km.施工前2天修完1.2 km后,计划发生变化, 准备提前2天完成修路任务,以后几天内平均每天至少要修路多少?
解:设以后几天内平均每天至少要修路x千米.则
6x≥6-1.2
解得 x≥0.8
答:以后几天平均每天至少要修路 0.8千米.
达标测评
3.某公司要招甲、乙两种工作人员30人,甲种工作人员月薪600元,乙种工作人员月薪1000元.现要求每月总工资不能超过2.2万元,问至多可招乙种工作人员多少名?
解:设至多可招乙种工作人员x名,则甲种工作人员为(30-x)名,根据题意得:
600(30-x)+1000x≤22000
解得 x≤10
答:至多可招乙种工作人员10名.
