人教版数学七年级下册 第九章 一元一次不等式 培优课件(共30张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第九章 一元一次不等式 培优课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 22:08:21 | ||
图片预览











文档简介
第九章 一元一次不等式
本章例题精讲
C. D.
A. B.
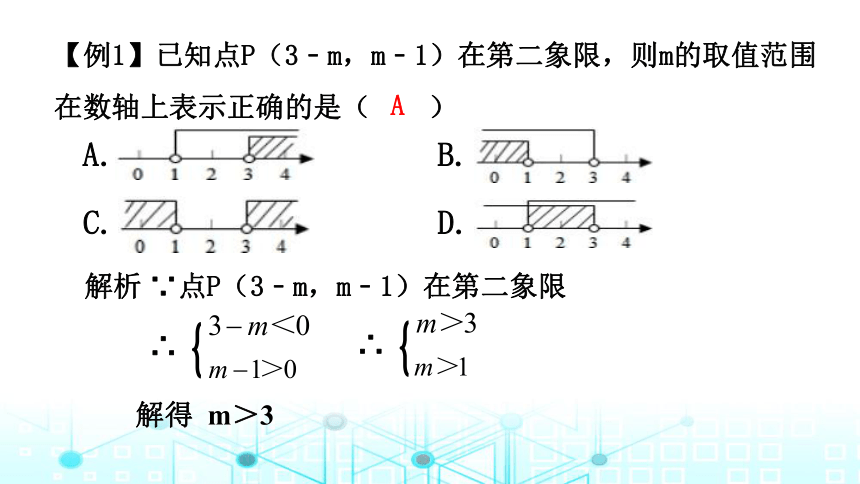
【例1】已知点P(3﹣m,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )
解得 m>3
解析 ∵点P(3﹣m,m﹣1)在第二象限
∴
A
∴
【练1】点 在第三象限,则x的取值范围是________.
∴
解得 m<-3
∴
解析 ∵点 在第三象限
m<-3
【变式1】平面坐标系中,点 关于x轴对称点在第四象限,的范围表示为( )
解得 0<a<2
∴
∴
解析 ∵ 关于x轴对称点在第四象限
∴ 在第一象限
A
A
【例2】关于x的不等式组 的解集为x>3,则a的取值范围是( )。
A、a≥-3 B、a≤-3 C、a>-3 D、a<-3
∴ -a≤3
解析:解原不等式组得解集为
∵不等式组 的解集为x>3
解得a≥3
【练2】如果一元一次不等式组 的解集为x>5,那么a的取值范围是 ( )
A. a>5 B. a≥5 C. a≤5 D. a<5
C
∴ a≤5
解析 ∵不等式组 的解集为x>5
【例3】已知关于x不等式组 无解,则a的取值范围是___
a≥3
∴ a≥3
解析:解原不等式组得解集为
∵不等式组 无解
【练3】如果不等式组 无解,那么不等式组 的解集是( )
A.2-b≤x≤2-a B.b-2≤x≤a-2
C.2-a≤x≤2-b D.无解
C
∴ 解集为2-a≤x≤2-b
∵ 不等式组 无解
∴ a≥b
解析 解不等式组 得解集为
∴ -a≤-b
∴ 2-a≤2-b
【例4】关于x的不等式组 只有4个整数解,则a的取值范围是( )
A.5≤a≤6 B.5≤a<6 C.5<a≤6 D.5<a<6
∴ 3< a-2≤4
解析:解原不等式组得解集为
∵不等式组 只有4个整数解(画数轴)
解得 5< a≤6
C
【练4】若关于x的不等式组 的整数解只有3个,则a的取值范围是( )
A. 3<a≤4 B. 2<a≤3 C. 2≤a<3 D. 3≤a<4
∴ 3< a+1≤4
解析:解原不等式组得解集为
解得 2< a≤3
B
∵不等式组 只有3个整数解(画数轴)
【变式4】已知关于x的不等式组 仅有三个整数解,则a的取值范围是( )
A. ≤a<1 B. ≤a≤1 C. <a≤1 D.a<1
∴ -2≤2a-3<-1
解析:解原不等式组得解集为
A
∵不等式组 只有3个整数解(画数轴)
解得 ≤a<1
A.10 B.7 C.6 D.0
【例5】不等式组 的所有非负整数解的和是( )
∴它们的和为:(-2)+(-1)+0+1+2+3+4=7
解析:解原不等式组得解集为 -2.5<x≤4
满足解集的负整数有-2,-1,0,1,2,3,4
B
【练5】写出一个解集为x>1的一元一次不等式________.
x-1>0
本章知识点归总
【例6】已知不等式组 有解,则a的取值范围为 ( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
解析:解不等式组得a≤x<2
∵不等式组 有解
∴ a<2
∴ m≥1.5
【练6】若不等式组 有解,则m的取值范围是__________。
m ≥1.5
解析:解不等式组得 1.5≤x≤m
∵不等式组 有解
【例7】如果不等式组 的解是x>3,那么m的取值范围是________.
m≤3
∴ m≤3
解析:解原不等式组得解集为
∵不等式组 的解是x>3
【练7】若关于x的一元一次不等式组 的解集是x≤a,那么a的取值范围是________.
a<5
∴ a<5
解析:解原不等式组得解集为
∵不等式组 的解是x≤a
【例8】若︱x+1︱= x+1,︱3x+2︱=-3x-2,则x的取值范围是_______
解: 由题意,得
∴ 这个不等式组的解集是
解得
A. B. C. D.
【练8】有数颗等重的糖果和数个大、小砝码,其中大砝码皆为5克、小砝码皆为1克,如图是将糖果与砝码放在等臂天平上的两种情形.判断下列哪一种情形是正确的( )
解析:由题意可得不等式组
解得 5<x<
则 10<2x<
15<3x<16
20<4x<
D符合题意
D
【例9】运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是 ( )
A.x≥11 B.11≤x<23 C.11解: 由题意,得第一次:2x+1≤95
解得
x≤47
第二次:2(2x+1)+1≤95
解得
x≤23
第三次:2[2(2x+1)+1]+1>95
解得
x>11
综上:11<x≤23
C
【练9】对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“结果是否大于88?”为一次操作.如果操作只进行两次就停止,则x的取值范围是________.
解: 由题意,得第一次:2x-10≤88
解得
x≤49
第二次:2(2x-10)-10>88
解得
x>29.5
综上:29.5<x≤49
29.5<x≤49
【例10】现规定一种运算:a※b=ab+a﹣b,其中a、b为常数,若2※3+m※1=6,则不等式 <m的解集是( )
A.x<﹣2 B.x<﹣1 C.x<0 D.x>2
解得 x<0
解析:∵ 2※3+m※1=6
∴ 2×3+2-3+m×1+m-1=6
∴ m=1
∴ <1
C
【练10】定义一种法则“#”如下:a#b= 例如:1#2=2.若(-2m-5) #3=3,则m的取值范围是__________.
解析: 由题意,得-2m-5≤3
解得
m≥-4
m≥-4
【例11】某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表.已知购进60双甲种运动鞋与50双乙种运动鞋共用10000元
运动鞋价格
甲
乙
进价(元/双)
m
m﹣20
售价(元/双)
240
160
(1)求m的值;
解析:由题意 60m+50(m-20)=10000
解得 m=100
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)超过21000元,且不超过22000元,问该专卖店有几种进货方案?
∴ 共有100-84+1=17种方案
解:设购进甲运动鞋x双,则购进乙运动鞋(200-x)双
由题意得
∵ x是正整数
解得 <x≤100
【练11】商场某柜台销售每台进价分别为160元、120元的A.B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A.B两种型号的电风扇的销售单价;
解:设A电风扇x元,B电风扇y元
由题意得
解得
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
解:设A种型电风扇采购m台,则B种型电风扇采购(50-m)台
由题意得
解得
160m+120(50-m)≤7500
m≤
∴ A种型号的电风扇最多能采购37台
由题意得
解得
(200-160)m+(150-120)(50-m)>1850
m>35
①当m=36时,50-m=14
又
m≤
∴
35<m≤
∵m为整数
∵m=36或37
②当m=37时,50-m=13
【例12】对于非负实数x“四舍五入”到个位的值记为,即:当n为非负整数时,若n- ≤x=n.如:<0>=<0.46>=0,<0.64>=<1.49>=1,<3.5>=<4.28>=4试解决下列问题:
(1)填空:①<π>= (π为圆周率)
②如果<2x-1>=3,那么实数x的取值范围_________
(2)试举例说明:当x= ,y= ,=+不恒成立;
(3)求满足= x的所有非负实数x的值.
解析 (1)填空: ①<π>=<3.14159626……>=3
② ∵<2x-1>=3
∴ 3- ≤2x-1<3+
解得 ≤x<
(2)如x=0.8,y=0.6时
=<0.8+0.6>=1
而+=<0.8>+<0.6>=2
此时≠+
(3)∵x≥0, x为整数
∴< k>=k
解得 0 ≤ k≤2
设 x=k,k为整数
则x= k
∴k - ≤ k<k+ ,k≥0
∴ k=0,1,2
∴ x=0, ,
【练12】我们用a表示不大于a的最大整数,例如:2.5=2,3=3,-2.5=-3;用〈a〉表示大于a的最小整数,例如: 〈2.5〉=3,〈4〉=5,〈-1.5〉=-1.据此解决下列问题:
(1)-4.5= , 〈3.5〉= ;
(2)若x=2,则x的取值范围是 ;若〈y〉=-1,则y的取值范围是 ;
(3)已知x,y满足方程组, ,求x,y的取值范围.
-5
4
2≤x<3
-2≤y<-1
解:(3)由
解得
∴x,y的取值范围分别为-1≤x<0,2≤y<3.
本章例题精讲
C. D.
A. B.
【例1】已知点P(3﹣m,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )
解得 m>3
解析 ∵点P(3﹣m,m﹣1)在第二象限
∴
A
∴
【练1】点 在第三象限,则x的取值范围是________.
∴
解得 m<-3
∴
解析 ∵点 在第三象限
m<-3
【变式1】平面坐标系中,点 关于x轴对称点在第四象限,的范围表示为( )
解得 0<a<2
∴
∴
解析 ∵ 关于x轴对称点在第四象限
∴ 在第一象限
A
A
【例2】关于x的不等式组 的解集为x>3,则a的取值范围是( )。
A、a≥-3 B、a≤-3 C、a>-3 D、a<-3
∴ -a≤3
解析:解原不等式组得解集为
∵不等式组 的解集为x>3
解得a≥3
【练2】如果一元一次不等式组 的解集为x>5,那么a的取值范围是 ( )
A. a>5 B. a≥5 C. a≤5 D. a<5
C
∴ a≤5
解析 ∵不等式组 的解集为x>5
【例3】已知关于x不等式组 无解,则a的取值范围是___
a≥3
∴ a≥3
解析:解原不等式组得解集为
∵不等式组 无解
【练3】如果不等式组 无解,那么不等式组 的解集是( )
A.2-b≤x≤2-a B.b-2≤x≤a-2
C.2-a≤x≤2-b D.无解
C
∴ 解集为2-a≤x≤2-b
∵ 不等式组 无解
∴ a≥b
解析 解不等式组 得解集为
∴ -a≤-b
∴ 2-a≤2-b
【例4】关于x的不等式组 只有4个整数解,则a的取值范围是( )
A.5≤a≤6 B.5≤a<6 C.5<a≤6 D.5<a<6
∴ 3< a-2≤4
解析:解原不等式组得解集为
∵不等式组 只有4个整数解(画数轴)
解得 5< a≤6
C
【练4】若关于x的不等式组 的整数解只有3个,则a的取值范围是( )
A. 3<a≤4 B. 2<a≤3 C. 2≤a<3 D. 3≤a<4
∴ 3< a+1≤4
解析:解原不等式组得解集为
解得 2< a≤3
B
∵不等式组 只有3个整数解(画数轴)
【变式4】已知关于x的不等式组 仅有三个整数解,则a的取值范围是( )
A. ≤a<1 B. ≤a≤1 C. <a≤1 D.a<1
∴ -2≤2a-3<-1
解析:解原不等式组得解集为
A
∵不等式组 只有3个整数解(画数轴)
解得 ≤a<1
A.10 B.7 C.6 D.0
【例5】不等式组 的所有非负整数解的和是( )
∴它们的和为:(-2)+(-1)+0+1+2+3+4=7
解析:解原不等式组得解集为 -2.5<x≤4
满足解集的负整数有-2,-1,0,1,2,3,4
B
【练5】写出一个解集为x>1的一元一次不等式________.
x-1>0
本章知识点归总
【例6】已知不等式组 有解,则a的取值范围为 ( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
解析:解不等式组得a≤x<2
∵不等式组 有解
∴ a<2
∴ m≥1.5
【练6】若不等式组 有解,则m的取值范围是__________。
m ≥1.5
解析:解不等式组得 1.5≤x≤m
∵不等式组 有解
【例7】如果不等式组 的解是x>3,那么m的取值范围是________.
m≤3
∴ m≤3
解析:解原不等式组得解集为
∵不等式组 的解是x>3
【练7】若关于x的一元一次不等式组 的解集是x≤a,那么a的取值范围是________.
a<5
∴ a<5
解析:解原不等式组得解集为
∵不等式组 的解是x≤a
【例8】若︱x+1︱= x+1,︱3x+2︱=-3x-2,则x的取值范围是_______
解: 由题意,得
∴ 这个不等式组的解集是
解得
A. B. C. D.
【练8】有数颗等重的糖果和数个大、小砝码,其中大砝码皆为5克、小砝码皆为1克,如图是将糖果与砝码放在等臂天平上的两种情形.判断下列哪一种情形是正确的( )
解析:由题意可得不等式组
解得 5<x<
则 10<2x<
15<3x<16
20<4x<
D符合题意
D
【例9】运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是 ( )
A.x≥11 B.11≤x<23 C.11
解得
x≤47
第二次:2(2x+1)+1≤95
解得
x≤23
第三次:2[2(2x+1)+1]+1>95
解得
x>11
综上:11<x≤23
C
【练9】对一个实数x按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“结果是否大于88?”为一次操作.如果操作只进行两次就停止,则x的取值范围是________.
解: 由题意,得第一次:2x-10≤88
解得
x≤49
第二次:2(2x-10)-10>88
解得
x>29.5
综上:29.5<x≤49
29.5<x≤49
【例10】现规定一种运算:a※b=ab+a﹣b,其中a、b为常数,若2※3+m※1=6,则不等式 <m的解集是( )
A.x<﹣2 B.x<﹣1 C.x<0 D.x>2
解得 x<0
解析:∵ 2※3+m※1=6
∴ 2×3+2-3+m×1+m-1=6
∴ m=1
∴ <1
C
【练10】定义一种法则“#”如下:a#b= 例如:1#2=2.若(-2m-5) #3=3,则m的取值范围是__________.
解析: 由题意,得-2m-5≤3
解得
m≥-4
m≥-4
【例11】某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表.已知购进60双甲种运动鞋与50双乙种运动鞋共用10000元
运动鞋价格
甲
乙
进价(元/双)
m
m﹣20
售价(元/双)
240
160
(1)求m的值;
解析:由题意 60m+50(m-20)=10000
解得 m=100
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)超过21000元,且不超过22000元,问该专卖店有几种进货方案?
∴ 共有100-84+1=17种方案
解:设购进甲运动鞋x双,则购进乙运动鞋(200-x)双
由题意得
∵ x是正整数
解得 <x≤100
【练11】商场某柜台销售每台进价分别为160元、120元的A.B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A.B两种型号的电风扇的销售单价;
解:设A电风扇x元,B电风扇y元
由题意得
解得
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
解:设A种型电风扇采购m台,则B种型电风扇采购(50-m)台
由题意得
解得
160m+120(50-m)≤7500
m≤
∴ A种型号的电风扇最多能采购37台
由题意得
解得
(200-160)m+(150-120)(50-m)>1850
m>35
①当m=36时,50-m=14
又
m≤
∴
35<m≤
∵m为整数
∵m=36或37
②当m=37时,50-m=13
【例12】对于非负实数x“四舍五入”到个位的值记为
(1)填空:①<π>= (π为圆周率)
②如果<2x-1>=3,那么实数x的取值范围_________
(2)试举例说明:当x= ,y= ,
(3)求满足
解析 (1)填空: ①<π>=<3.14159626……>=3
② ∵<2x-1>=3
∴ 3- ≤2x-1<3+
解得 ≤x<
(2)如x=0.8,y=0.6时
而
此时
(3)∵x≥0, x为整数
∴< k>=k
解得 0 ≤ k≤2
设 x=k,k为整数
则x= k
∴k - ≤ k<k+ ,k≥0
∴ k=0,1,2
∴ x=0, ,
【练12】我们用a表示不大于a的最大整数,例如:2.5=2,3=3,-2.5=-3;用〈a〉表示大于a的最小整数,例如: 〈2.5〉=3,〈4〉=5,〈-1.5〉=-1.据此解决下列问题:
(1)-4.5= , 〈3.5〉= ;
(2)若x=2,则x的取值范围是 ;若〈y〉=-1,则y的取值范围是 ;
(3)已知x,y满足方程组, ,求x,y的取值范围.
-5
4
2≤x<3
-2≤y<-1
解:(3)由
解得
∴x,y的取值范围分别为-1≤x<0,2≤y<3.
