人教数学七年级下册第8章8.3.2实际问题与二元一次方程组(共17张PPT)
文档属性
| 名称 | 人教数学七年级下册第8章8.3.2实际问题与二元一次方程组(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 260.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-29 22:06:29 | ||
图片预览



文档简介
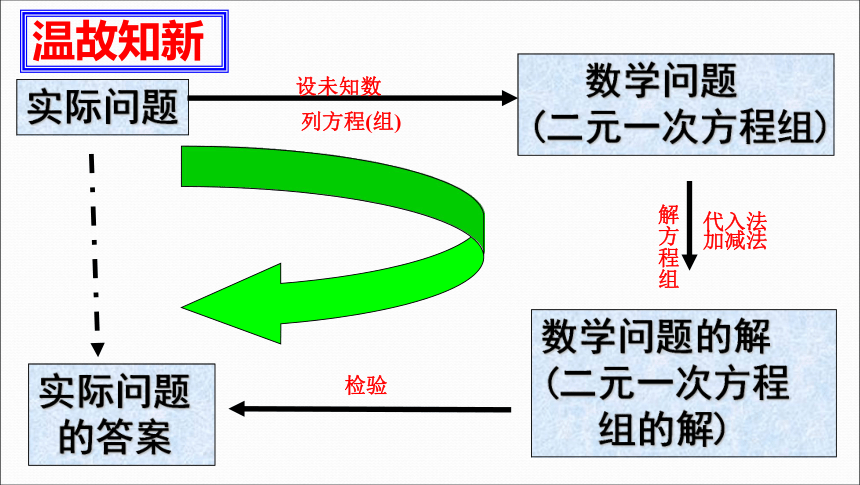
8.3 实际问题与二元一次方程组(3)
实际问题
数学问题
(二元一次方程组)
数学问题的解(二元一次方程
组的解)
检验
实际问题
的答案
设未知数
列方程(组)
解方程组
代入法
加减法
温故知新
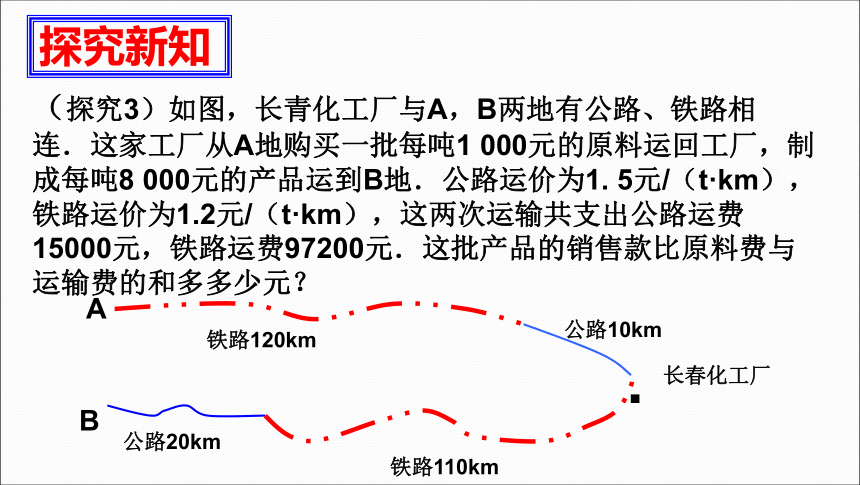
(探究3)如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
探究新知
活动一 :
货车拉货,每吨每千米运费为3元,记为:3元/(吨·千米),
1.运价“1.5元∕(t·km)”的含义
(1)运5吨货物走1千米需运输费: 元
(2)运5吨货物走10千米需运输费: 元
(3)运x吨货物走y千米需运输费: 元
15
150
3xy
运输费=运价×货物重量×路程
公路运费:15000元 铁路运费:97200元
公路运价:1.5元/(吨·千米)
铁路运价:1.2元/(吨·千米)
原料单价:1000元/吨
产品单价:8000元/吨
(由图可知) 原料在公路运输路程:10千米
原料在铁路运输路程:120千米
产品在公路运输路程:20千米
产品在铁路运输路程:110千米
2.已知的量:
(由题可知)
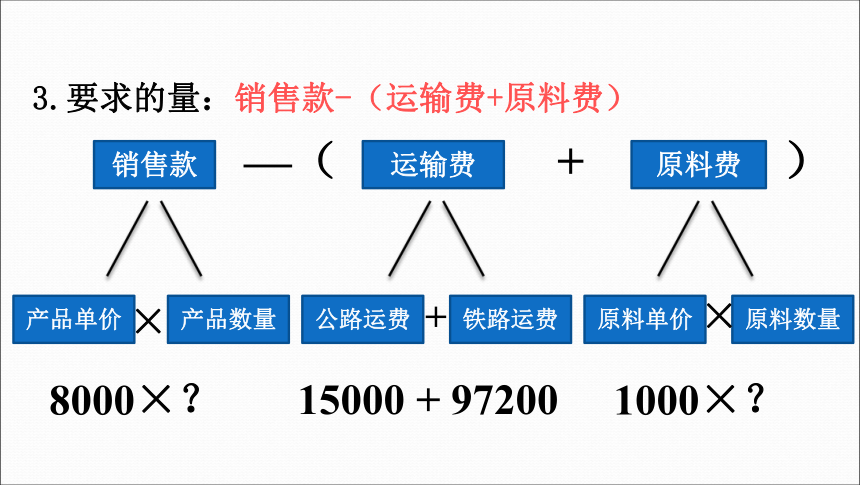
3.要求的量:销售款-(运输费+原料费)
销售款
—( + )
运输费
原料费
产品单价
产品数量
公路运费
铁路运费
原料单价
原料数量
×
+
×
8000×?
15000 + 97200
1000×?
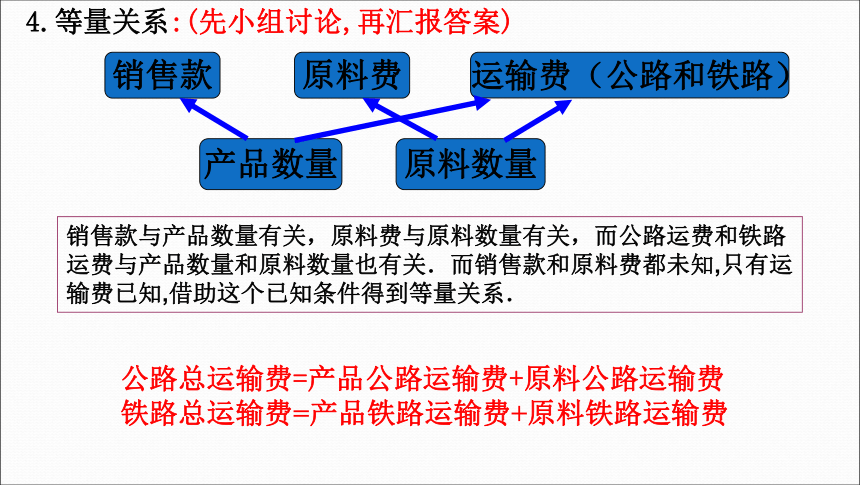
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量也有关.而销售款和原料费都未知,只有运输费已知,借助这个已知条件得到等量关系.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
4.等量关系:(先小组讨论,再汇报答案)
公路总运输费=产品公路运输费+原料公路运输费
铁路总运输费=产品铁路运输费+原料铁路运输费
问题1、原料的数量与产品的数量一样多吗?
(不一样多)
问题2、那些量设为未知数?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此设 .
产品 吨重,原料 吨重
问题3、本题涉及的量较多,这种情况下常用列表的方式来处理,列 表直观、简洁(先小组填写,再汇报答案).
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
活动二:
是原方程组的解.
先化简,得
②
①
由①,得
代入③ ,得
③
代入② ,得
解:设制成产品x t,购买原料y t。
活动三:
这个实际问题的答案是什么?
销售款:8 000 x= 8000×300=2 400 000;
原料费:1 000 y=1000×400=400 000;
运输费:15 000+97 200=112 200.
所以销售款比原料费与运输费的和多:
2400000-(400000+112200)=1887800(元)答:这批产品的销售款比原料费与运输费的和多1 887 800元.
活动四:
回顾上题的解决过程,你应该怎样设定未知数?
如何更好地分析“探究3”这样数量关系比较复杂的实际问题?
当直接将所求的结果当作未知数无法列出方程时,考虑选择设间接未知数.
利用列表法解决数量关系比较复杂的实际问题
通过本节课的学习,
你又有哪些新的收获?
还有什么疑惑?
课堂小结
1、一批蔬菜要运往某批发市场,菜农准备租用汽车公司的甲、乙两种货车.已知过去两次租用这两种货车的记录如下表所示.
这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完,如果每吨付20元运费,问:菜农应付运费多少元?
知识迁移
甲种货车(辆)
乙种货车(辆)
总量(吨)
第1次
4
5
35
第2次
3
6
33
答:要刚好一次运完,菜农应付运费620元。
解:设甲种货车每辆可运x吨,乙种货车每辆可运y吨,则
4x+5y=35
3x+6y=33
{
解之得
{
x=5,
y=3,
(5x+2y) 20 = (5 5 + 2 3) 20 = 620(元)
×
×
×
×
布置作业
教科书 习题8.3 第5、8题
1.某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组( )
当堂检测
B.
C.
D.
A.
捐款(元)
2
3
4
5
人数
6
7
2.用1块A型钢板可制成2块C型钢板,1块D型钢板;用1块B型钢板可制成1块C型钢板,2块D型钢板.现需15块C型钢板,18块D型钢板,可恰好用A型钢板,B型钢板各多少块?
实际问题
数学问题
(二元一次方程组)
数学问题的解(二元一次方程
组的解)
检验
实际问题
的答案
设未知数
列方程(组)
解方程组
代入法
加减法
温故知新
(探究3)如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
探究新知
活动一 :
货车拉货,每吨每千米运费为3元,记为:3元/(吨·千米),
1.运价“1.5元∕(t·km)”的含义
(1)运5吨货物走1千米需运输费: 元
(2)运5吨货物走10千米需运输费: 元
(3)运x吨货物走y千米需运输费: 元
15
150
3xy
运输费=运价×货物重量×路程
公路运费:15000元 铁路运费:97200元
公路运价:1.5元/(吨·千米)
铁路运价:1.2元/(吨·千米)
原料单价:1000元/吨
产品单价:8000元/吨
(由图可知) 原料在公路运输路程:10千米
原料在铁路运输路程:120千米
产品在公路运输路程:20千米
产品在铁路运输路程:110千米
2.已知的量:
(由题可知)
3.要求的量:销售款-(运输费+原料费)
销售款
—( + )
运输费
原料费
产品单价
产品数量
公路运费
铁路运费
原料单价
原料数量
×
+
×
8000×?
15000 + 97200
1000×?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量也有关.而销售款和原料费都未知,只有运输费已知,借助这个已知条件得到等量关系.
销售款
原料费
运输费(公路和铁路)
产品数量
原料数量
4.等量关系:(先小组讨论,再汇报答案)
公路总运输费=产品公路运输费+原料公路运输费
铁路总运输费=产品铁路运输费+原料铁路运输费
问题1、原料的数量与产品的数量一样多吗?
(不一样多)
问题2、那些量设为未知数?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此设 .
产品 吨重,原料 吨重
问题3、本题涉及的量较多,这种情况下常用列表的方式来处理,列 表直观、简洁(先小组填写,再汇报答案).
产品x吨
原料y吨
合计
公路运费(元)
铁路运费(元)
价值(元)
活动二:
是原方程组的解.
先化简,得
②
①
由①,得
代入③ ,得
③
代入② ,得
解:设制成产品x t,购买原料y t。
活动三:
这个实际问题的答案是什么?
销售款:8 000 x= 8000×300=2 400 000;
原料费:1 000 y=1000×400=400 000;
运输费:15 000+97 200=112 200.
所以销售款比原料费与运输费的和多:
2400000-(400000+112200)=1887800(元)答:这批产品的销售款比原料费与运输费的和多1 887 800元.
活动四:
回顾上题的解决过程,你应该怎样设定未知数?
如何更好地分析“探究3”这样数量关系比较复杂的实际问题?
当直接将所求的结果当作未知数无法列出方程时,考虑选择设间接未知数.
利用列表法解决数量关系比较复杂的实际问题
通过本节课的学习,
你又有哪些新的收获?
还有什么疑惑?
课堂小结
1、一批蔬菜要运往某批发市场,菜农准备租用汽车公司的甲、乙两种货车.已知过去两次租用这两种货车的记录如下表所示.
这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完,如果每吨付20元运费,问:菜农应付运费多少元?
知识迁移
甲种货车(辆)
乙种货车(辆)
总量(吨)
第1次
4
5
35
第2次
3
6
33
答:要刚好一次运完,菜农应付运费620元。
解:设甲种货车每辆可运x吨,乙种货车每辆可运y吨,则
4x+5y=35
3x+6y=33
{
解之得
{
x=5,
y=3,
(5x+2y) 20 = (5 5 + 2 3) 20 = 620(元)
×
×
×
×
布置作业
教科书 习题8.3 第5、8题
1.某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.
若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组( )
当堂检测
B.
C.
D.
A.
捐款(元)
2
3
4
5
人数
6
7
2.用1块A型钢板可制成2块C型钢板,1块D型钢板;用1块B型钢板可制成1块C型钢板,2块D型钢板.现需15块C型钢板,18块D型钢板,可恰好用A型钢板,B型钢板各多少块?
