(试题4)24.3正多边形和圆
文档属性
| 名称 | (试题4)24.3正多边形和圆 |
|
|
| 格式 | zip | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-20 00:00:00 | ||
图片预览

文档简介
24.3正多边形和圆
一、认认真真,书写快乐
1.正三角形的内切圆半径、外接圆半径和高的比为 .
2.边长为a的正六边形的边心距是 ,周长是 ,面积是 .
3.一个正方形和一个正六边形的外接圆半径相等,则此正方形与正六边形的面积之比为 .
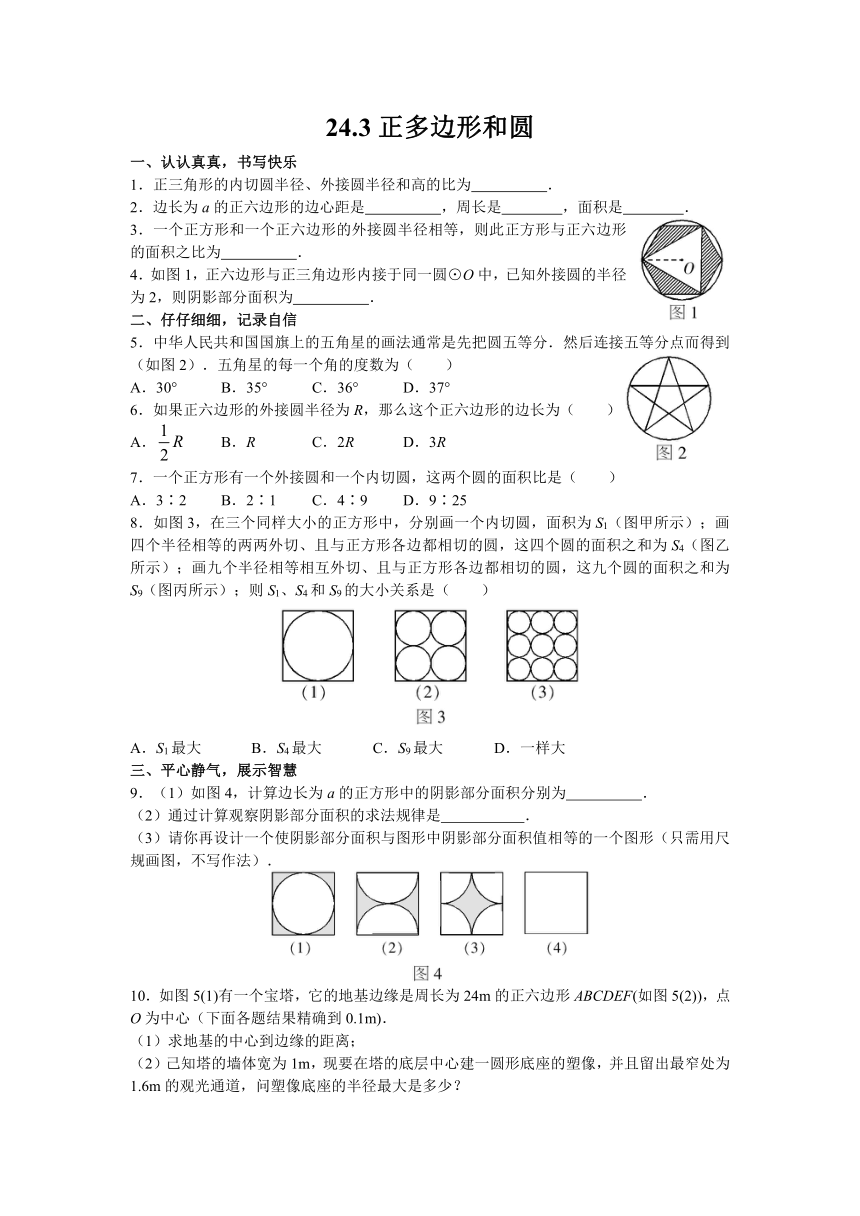
4.如图1,正六边形与正三角边形内接于同一圆⊙O中,已知外接圆的半径为2,则阴影部分面积为 .
二、仔仔细细,记录自信
5.中华人民共和国国旗上的五角星的画法通常是先把圆五等分.然后连接五等分点而得到(如图2).五角星的每一个角的度数为( )
A.30° B.35° C.36° D.37°
6.如果正六边形的外接圆半径为R,那么这个正六边形的边长为( )
A. B.R C.2R D.3R
7.一个正方形有一个外接圆和一个内切圆,这两个圆的面积比是( )
A.3∶2 B.2∶1 C.4∶9 D.9∶25
8.如图3,在三个同样大小的正方形中,分别画一个内切圆,面积为S1(图甲所示);画四个半径相等的两两外切、且与正方形各边都相切的圆,这四个圆的面积之和为S4(图乙所示);画九个半径相等相互外切、且与正方形各边都相切的圆,这九个圆的面积之和为S9(图丙所示);则S1、S4和S9的大小关系是( )
A.S1最大 B.S4最大 C.S9最大 D.一样大
三、平心静气,展示智慧
9.(1)如图4,计算边长为a的正方形中的阴影部分面积分别为 .
(2)通过计算观察阴影部分面积的求法规律是 .
(3)请你再设计一个使阴影部分面积与图形中阴影部分面积值相等的一个图形(只需用尺规画图,不写作法).
10.如图5(1)有一个宝塔,它的地基边缘是周长为24m的正六边形ABCDEF(如图5(2)),点O为中心(下面各题结果精确到0.1m).
(1)求地基的中心到边缘的距离;
(2)己知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?
四、拓广探索,游刃有余
11.如图6(1)、图6(2)、图6(3)、…、图6(n),M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.
(1)求图6(1)中∠MON的度数;
(2)图6(2)中∠MON的度数是 ,图6(3)中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
参考答案:
一、1.1:2:3 2.;; 3. 4.
二、5.C 6.B 7.B 8.D
三、9.解:(1);;;
(2)阴影部分面积的求法规律是;
(3)略.
10.地基的中心到边缘的距离约为3.5m;塑像底座的半径最大约为0.9m.
四、11.解:(1).(2);.
(3)通过以上计算及存在的规律答容易确定.
一、认认真真,书写快乐
1.正三角形的内切圆半径、外接圆半径和高的比为 .
2.边长为a的正六边形的边心距是 ,周长是 ,面积是 .
3.一个正方形和一个正六边形的外接圆半径相等,则此正方形与正六边形的面积之比为 .
4.如图1,正六边形与正三角边形内接于同一圆⊙O中,已知外接圆的半径为2,则阴影部分面积为 .
二、仔仔细细,记录自信
5.中华人民共和国国旗上的五角星的画法通常是先把圆五等分.然后连接五等分点而得到(如图2).五角星的每一个角的度数为( )
A.30° B.35° C.36° D.37°
6.如果正六边形的外接圆半径为R,那么这个正六边形的边长为( )
A. B.R C.2R D.3R
7.一个正方形有一个外接圆和一个内切圆,这两个圆的面积比是( )
A.3∶2 B.2∶1 C.4∶9 D.9∶25
8.如图3,在三个同样大小的正方形中,分别画一个内切圆,面积为S1(图甲所示);画四个半径相等的两两外切、且与正方形各边都相切的圆,这四个圆的面积之和为S4(图乙所示);画九个半径相等相互外切、且与正方形各边都相切的圆,这九个圆的面积之和为S9(图丙所示);则S1、S4和S9的大小关系是( )
A.S1最大 B.S4最大 C.S9最大 D.一样大
三、平心静气,展示智慧
9.(1)如图4,计算边长为a的正方形中的阴影部分面积分别为 .
(2)通过计算观察阴影部分面积的求法规律是 .
(3)请你再设计一个使阴影部分面积与图形中阴影部分面积值相等的一个图形(只需用尺规画图,不写作法).
10.如图5(1)有一个宝塔,它的地基边缘是周长为24m的正六边形ABCDEF(如图5(2)),点O为中心(下面各题结果精确到0.1m).
(1)求地基的中心到边缘的距离;
(2)己知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?
四、拓广探索,游刃有余
11.如图6(1)、图6(2)、图6(3)、…、图6(n),M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.
(1)求图6(1)中∠MON的度数;
(2)图6(2)中∠MON的度数是 ,图6(3)中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
参考答案:
一、1.1:2:3 2.;; 3. 4.
二、5.C 6.B 7.B 8.D
三、9.解:(1);;;
(2)阴影部分面积的求法规律是;
(3)略.
10.地基的中心到边缘的距离约为3.5m;塑像底座的半径最大约为0.9m.
四、11.解:(1).(2);.
(3)通过以上计算及存在的规律答容易确定.
同课章节目录
