(试题2)24.3~24.4随堂练习
文档属性
| 名称 | (试题2)24.3~24.4随堂练习 |  | |
| 格式 | zip | ||
| 文件大小 | 136.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-20 23:55:31 | ||
图片预览

文档简介
九年级上册24.3正多边形和圆
一、选择题
1、如图1,若正△A1B1C1内接于正△ABC的内切圆,则的值为( )
(A) (B) (C) (D)
2、正多边形的一边所对的中心角与该正多边形的一个外角的关系是( )
A、两角互余 B、两角互补 C、两角互余或互补 D、不能确定
3、圆的半径扩大一倍,则它的相应的内接正六边形的边长和半径的比( )
A、缩小了一倍 B、扩大了一倍 C、扩大了两倍 D、没有扩大也没有缩小
4、若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于( )
(A) (B) (C) (D)
二、填空题
5、一个正三角形的边长为a,则它的内切圆和外接圆的组成的圆环的面积是 。
6、已知一个正多边形的一个外角为90°,则它的边心距与半径的比为 。
7、正三角形的外接圆的半径为4,以正三角形的一边为边的正方形的外接圆的半径是 。
8、已知正六边形ABCDEF的半径为12,则这个正六边形的内切圆的面积是 。
三、解答题
9、如图2所示,△ABC是⊙O的内接正三角形,五边形ADEFG是⊙O的内接正五边形,求证:BE是⊙O的内接正十五边形。
四、拓广探索
10、如图,一个圆形的花园,有三个出口A、B、C,每两个出口之间有一条60米的道路,组成正三角形ABC,在中心点O处有一个亭子,为使亭子和原有的道路相通,再需修三条小路OD、OE、OF,使另一出口分别在△ABC的三边上,且这条小路把△ABC分成全等的多边形,已被种植不同品种的花草。
(1)请你按照以上要求设计一种方案,将你的设计方案分别画在图3上,并附简短的说明;
(2)要使三条小路把△ABC分成三个全等的等腰梯形,应怎样设计?请把方案画在图4中,并求此时三条小路的总长;
(3)请你探究出一种一般方法,使得出口D不论在什么位置,都能准确地找到另外两个出口E、F的位置,请写明这个方法;(图5供你探究)
(4)你在(3)中探究出的一般方法适用于正五边形吗?请结合图6予以说明。这种方法能推广到正n边形吗?
11、某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行了如下的讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形;
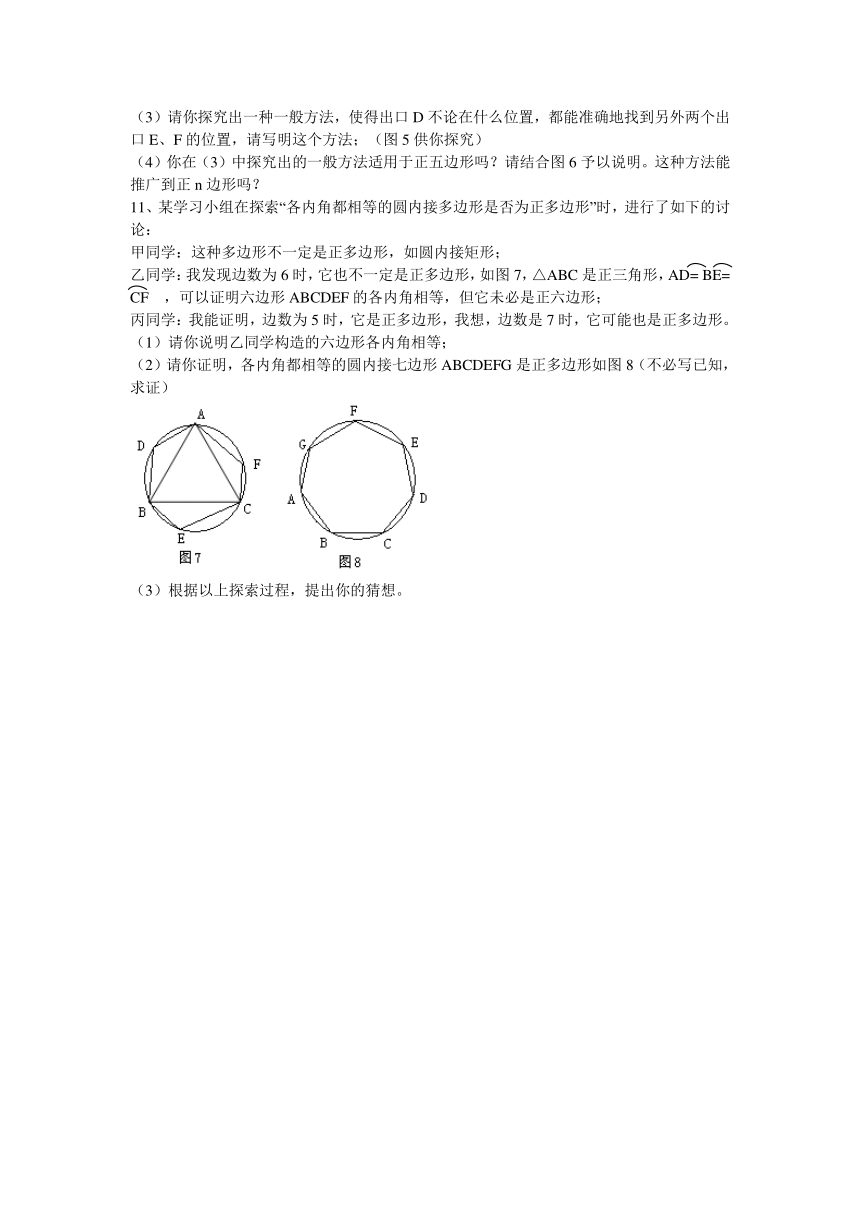
乙同学:我发现边数为6时,它也不一定是正多边形,如图7,△ABC是正三角形,AD= BE= CF ,可以证明六边形ABCDEF的各内角相等,但它未必是正六边形;
丙同学:我能证明,边数为5时,它是正多边形,我想,边数是7时,它可能也是正多边形。
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG是正多边形如图8(不必写已知,求证)
(3)根据以上探索过程,提出你的猜想。
24.4弧长与扇形公式
一、选择题
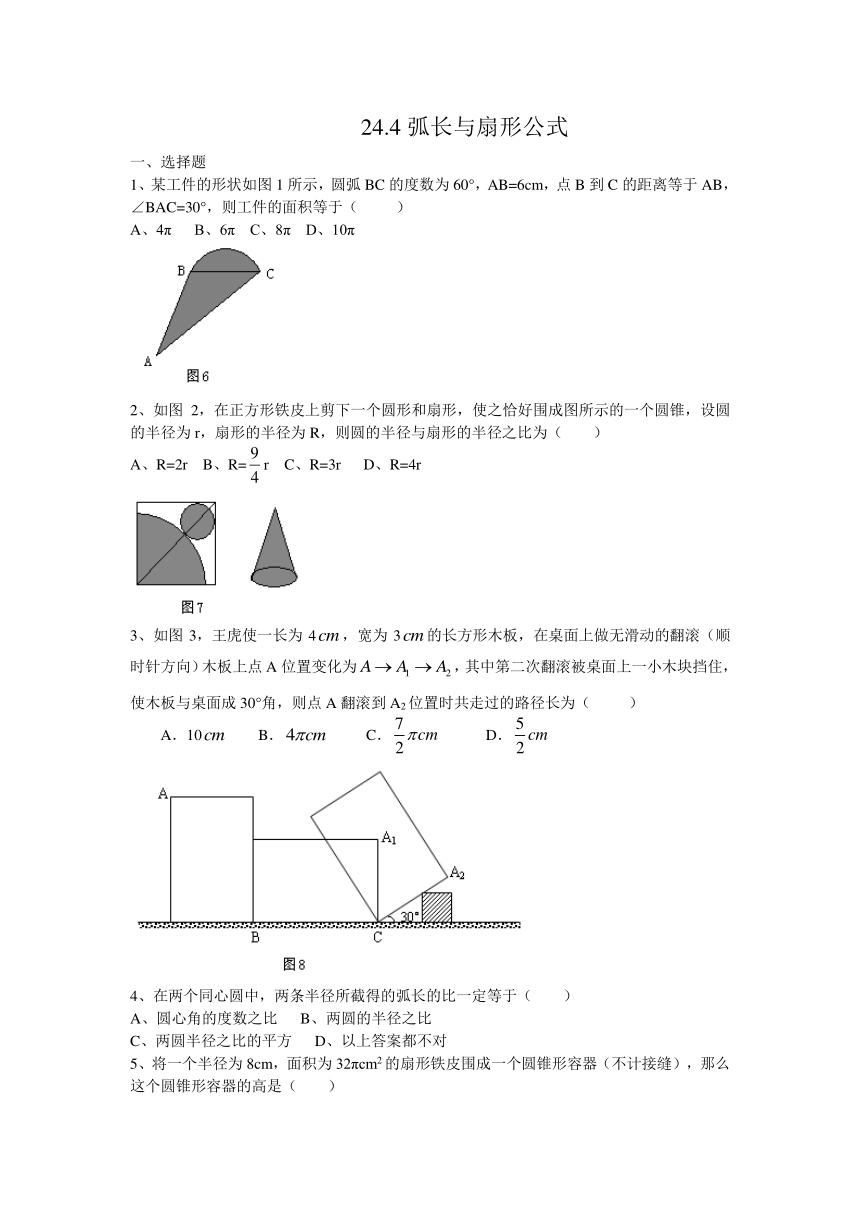
1、某工件的形状如图1所示,圆弧BC的度数为60°,AB=6cm,点B到C的距离等于AB,∠BAC=30°,则工件的面积等于( )
A、4π B、6π C、8π D、10π
( http: / / www. / Index.html )
2、如图2,在正方形铁皮上剪下一个圆形和扇形,使之恰好围成图所示的一个圆锥,设圆的半径为r,扇形的半径为R,则圆的半径与扇形的半径之比为( )
A、R=2r B、R=r C、R=3r D、R=4r
3、如图3,王虎使一长为4,宽为3的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.10 B. C. D.
( http: / / www. / Index.html )
4、在两个同心圆中,两条半径所截得的弧长的比一定等于( )
A、圆心角的度数之比 B、两圆的半径之比
C、两圆半径之比的平方 D、以上答案都不对
5、将一个半径为8cm,面积为32πcm2的扇形铁皮围成一个圆锥形容器(不计接缝),那么这个圆锥形容器的高是( )
A、4 B、4 C、4 D、2
二、填空题
6、图4是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽
的纸的面积为 cm2(π取3.14)。
7、图5⑴、图5⑵是两种方法把6根圆形钢管用钢丝捆扎的截面
图。设图⑴、图⑵两种方法捆扎所需钢丝绳的长度是a、b(不记
接头部分),则a、b的大小关系为:a________b(填“<”、
“=”或“>”)。
8、如图6,中,,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为 。
( http: / / www. / Index.html )
9、如图7,有一个圆锥形的粮仓,从正面看是边长为6cm的正三角形ABC,母线AC的中点P外有一老鼠正在偷吃粮食,小猫从B处沿着圆锥的表面去偷袭老鼠,则小猫经过的最短路程是 m。(结果不取近似数)。
10、如图8,⊙O1的半径O1A是⊙O2 的直径,⊙O1的半径O1C交⊙O2于点B,则
AC和 AB 的长度的大小关系是 。
三、拓广探索
11、如图9,有一跑道如图所示,(尺寸单位是:m),若起点设在A处,一同学沿着图中的虚线跑3000米,估算终点落在A、B、C、D的哪一点?
12、国际奥运会会旗上的图案是由代表五大洲的五个圆环组在一起,如图10所示,其中每个圆环上内外圆直径分别为8 和10,图中两两相交成的小曲边四边形的面积相等,已知五个圆环覆盖的面积是122.5 平方单位,请计算出每个小曲边四边形的面积(π取3.14)。
13、AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长 L=πa,计算:
(1)如图11甲,把AB分成两条相等的线段,每个小圆的周长l2= ;
(2)如图11乙,把AB分成三条相等的线段,每个小圆的周长l3= ;
(3)如图11丙,把AB分成四条相等的线段,每个小圆的周长l4= ;
(4)如图11丁,把AB分成n条相等的线段,每个小圆的周长ln= ;
结论:把大圆的直径分成几条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆的周长的 ;
( http: / / www. / Index.html )
请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系。
参考答案:
24.3
一、
1、A。2、B.3、D。4、A。
二、5、a2。6、1:。7、4。8、108π。
三、
9、连结OB、OE,∵△ABC是⊙O的内接正三角形,∴ AB 的度数为×360°=120°,∵正五边形ADEFG是⊙O的内接正五边形,∴AD 和DE 的度数都等于×360°=72°,∴AE 的度数为144°,BE 的度数为144°-120°=24°, ∴∠BOE=24°,∵正十五边形的中心角是24°,∴∠BOE就是⊙O的正十五边形的中心角,则BE即是正十五边形的边长。
10、解:(1)方案如图3,OE、OF、OG分别与AB、BC、AC垂直于D、E、F,得到OD、OE、OF三条小路。
(2)如图4,三条小路OD、OE、OF分别和AB、BC、AC平行,得到三个全等的等腰梯形。作OM⊥BC于点M,连结BO,∵△ABC是等边三角形,∴BM=BC=30,且∠OBM=30°,在Rt△OBM中,则OB=2OM,则由勾股定理可得OM=10,在Rt△OME中,∵OE∥AB,∠OEM=∠ABC=30°,同样利用勾股定理可得OE=20,又因OE=OF=OD,∴OE+OF+OD=3OE=60。即此时这三条路的总长为60米。
(3)如图5,在BC、CA、AB上分别截取BE=CF=AD,连结OD、OE、OF,即得3条小路。
(4)如图6,设M1,为A1A2边上的任意一点,如图6,在各边上分别截取A2M2=A3M3=A4M4=A5M5=A1M1,连结OM1、OM2、OM3、OM4、OM5,即可得到5条小路。因此可知能推广到正n边形。
四、
11、由图7可知 ∠AFC对ABC,因为 AD= CF,而∠DAF对的DEF=DBC+CF=AD+DBC=ABC,所以∠AFC=∠DAF,同理可证其余各角相等,所以图6中的六边形各内角相等。
(2)因为∠A对 BEG,∠B对CEA,且∠A=∠B,所以 BEG= CEA,所以BC=AG,同理可得
AB= CD= EF= AG= BC= DE =FG,所以其边形ABCDEFG是正七边形。
(3)猜想:当边数为奇数时,各内角相等的圆内接多边形是正多边形。
24.4答案:
一、
1、B。2、D。3、C。4、B。5、B。
二、
6、942。7、=。8、2π-2。9、3。10、相等。
三、
11、解:由题意知弯道长:LBC=LAD=2× HYPERLINK "http://www./Index.html" EMBED Equation.3 +≈101.4(m),所以跑到全长L=2AB+2LAB≈400(m),∴跑完3000米应是7圈零200米,而AB+LBC=200米固执终点应在C处。
12、解:五个圆环的覆盖部分的面积S5=5×[π()2-π()2]=45π=45×3.14=141.3。所以重叠在五个圆环上的8个小曲四边形的面积之和为S8=S5-122.5=18.8,即每个小曲四边形的面积是S8=2.35(平方单位)。
13、解:(1)=;==;==;==。
结论:每个小圆周长是大圆周长的。
设⊙O的面积为S,则S=π×()2=πa2,把AB分成两条相等的线段,每个小圆的面积S2=π×()2=πa2=S;把AB分成三条相等的线段,每个小圆的面积是S3=π×(×)2=πa2=S;把AB分成四条相等的线段,每个小圆的面积是S4=π×(×)2=πa2=S;把AB分成n条相等的线段,每个小圆的面积是Sn=π×(×)2=S;即每个小圆的面积是大圆的面积的。
20cm
30cm
图4
一、选择题
1、如图1,若正△A1B1C1内接于正△ABC的内切圆,则的值为( )
(A) (B) (C) (D)
2、正多边形的一边所对的中心角与该正多边形的一个外角的关系是( )
A、两角互余 B、两角互补 C、两角互余或互补 D、不能确定
3、圆的半径扩大一倍,则它的相应的内接正六边形的边长和半径的比( )
A、缩小了一倍 B、扩大了一倍 C、扩大了两倍 D、没有扩大也没有缩小
4、若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3,r4,r6,则r3:r4:r6等于( )
(A) (B) (C) (D)
二、填空题
5、一个正三角形的边长为a,则它的内切圆和外接圆的组成的圆环的面积是 。
6、已知一个正多边形的一个外角为90°,则它的边心距与半径的比为 。
7、正三角形的外接圆的半径为4,以正三角形的一边为边的正方形的外接圆的半径是 。
8、已知正六边形ABCDEF的半径为12,则这个正六边形的内切圆的面积是 。
三、解答题
9、如图2所示,△ABC是⊙O的内接正三角形,五边形ADEFG是⊙O的内接正五边形,求证:BE是⊙O的内接正十五边形。
四、拓广探索
10、如图,一个圆形的花园,有三个出口A、B、C,每两个出口之间有一条60米的道路,组成正三角形ABC,在中心点O处有一个亭子,为使亭子和原有的道路相通,再需修三条小路OD、OE、OF,使另一出口分别在△ABC的三边上,且这条小路把△ABC分成全等的多边形,已被种植不同品种的花草。
(1)请你按照以上要求设计一种方案,将你的设计方案分别画在图3上,并附简短的说明;
(2)要使三条小路把△ABC分成三个全等的等腰梯形,应怎样设计?请把方案画在图4中,并求此时三条小路的总长;
(3)请你探究出一种一般方法,使得出口D不论在什么位置,都能准确地找到另外两个出口E、F的位置,请写明这个方法;(图5供你探究)
(4)你在(3)中探究出的一般方法适用于正五边形吗?请结合图6予以说明。这种方法能推广到正n边形吗?
11、某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行了如下的讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形;
乙同学:我发现边数为6时,它也不一定是正多边形,如图7,△ABC是正三角形,AD= BE= CF ,可以证明六边形ABCDEF的各内角相等,但它未必是正六边形;
丙同学:我能证明,边数为5时,它是正多边形,我想,边数是7时,它可能也是正多边形。
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG是正多边形如图8(不必写已知,求证)
(3)根据以上探索过程,提出你的猜想。
24.4弧长与扇形公式
一、选择题
1、某工件的形状如图1所示,圆弧BC的度数为60°,AB=6cm,点B到C的距离等于AB,∠BAC=30°,则工件的面积等于( )
A、4π B、6π C、8π D、10π
( http: / / www. / Index.html )
2、如图2,在正方形铁皮上剪下一个圆形和扇形,使之恰好围成图所示的一个圆锥,设圆的半径为r,扇形的半径为R,则圆的半径与扇形的半径之比为( )
A、R=2r B、R=r C、R=3r D、R=4r
3、如图3,王虎使一长为4,宽为3的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.10 B. C. D.
( http: / / www. / Index.html )
4、在两个同心圆中,两条半径所截得的弧长的比一定等于( )
A、圆心角的度数之比 B、两圆的半径之比
C、两圆半径之比的平方 D、以上答案都不对
5、将一个半径为8cm,面积为32πcm2的扇形铁皮围成一个圆锥形容器(不计接缝),那么这个圆锥形容器的高是( )
A、4 B、4 C、4 D、2
二、填空题
6、图4是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽
的纸的面积为 cm2(π取3.14)。
7、图5⑴、图5⑵是两种方法把6根圆形钢管用钢丝捆扎的截面
图。设图⑴、图⑵两种方法捆扎所需钢丝绳的长度是a、b(不记
接头部分),则a、b的大小关系为:a________b(填“<”、
“=”或“>”)。
8、如图6,中,,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为 。
( http: / / www. / Index.html )
9、如图7,有一个圆锥形的粮仓,从正面看是边长为6cm的正三角形ABC,母线AC的中点P外有一老鼠正在偷吃粮食,小猫从B处沿着圆锥的表面去偷袭老鼠,则小猫经过的最短路程是 m。(结果不取近似数)。
10、如图8,⊙O1的半径O1A是⊙O2 的直径,⊙O1的半径O1C交⊙O2于点B,则
AC和 AB 的长度的大小关系是 。
三、拓广探索
11、如图9,有一跑道如图所示,(尺寸单位是:m),若起点设在A处,一同学沿着图中的虚线跑3000米,估算终点落在A、B、C、D的哪一点?
12、国际奥运会会旗上的图案是由代表五大洲的五个圆环组在一起,如图10所示,其中每个圆环上内外圆直径分别为8 和10,图中两两相交成的小曲边四边形的面积相等,已知五个圆环覆盖的面积是122.5 平方单位,请计算出每个小曲边四边形的面积(π取3.14)。
13、AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长 L=πa,计算:
(1)如图11甲,把AB分成两条相等的线段,每个小圆的周长l2= ;
(2)如图11乙,把AB分成三条相等的线段,每个小圆的周长l3= ;
(3)如图11丙,把AB分成四条相等的线段,每个小圆的周长l4= ;
(4)如图11丁,把AB分成n条相等的线段,每个小圆的周长ln= ;
结论:把大圆的直径分成几条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆的周长的 ;
( http: / / www. / Index.html )
请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系。
参考答案:
24.3
一、
1、A。2、B.3、D。4、A。
二、5、a2。6、1:。7、4。8、108π。
三、
9、连结OB、OE,∵△ABC是⊙O的内接正三角形,∴ AB 的度数为×360°=120°,∵正五边形ADEFG是⊙O的内接正五边形,∴AD 和DE 的度数都等于×360°=72°,∴AE 的度数为144°,BE 的度数为144°-120°=24°, ∴∠BOE=24°,∵正十五边形的中心角是24°,∴∠BOE就是⊙O的正十五边形的中心角,则BE即是正十五边形的边长。
10、解:(1)方案如图3,OE、OF、OG分别与AB、BC、AC垂直于D、E、F,得到OD、OE、OF三条小路。
(2)如图4,三条小路OD、OE、OF分别和AB、BC、AC平行,得到三个全等的等腰梯形。作OM⊥BC于点M,连结BO,∵△ABC是等边三角形,∴BM=BC=30,且∠OBM=30°,在Rt△OBM中,则OB=2OM,则由勾股定理可得OM=10,在Rt△OME中,∵OE∥AB,∠OEM=∠ABC=30°,同样利用勾股定理可得OE=20,又因OE=OF=OD,∴OE+OF+OD=3OE=60。即此时这三条路的总长为60米。
(3)如图5,在BC、CA、AB上分别截取BE=CF=AD,连结OD、OE、OF,即得3条小路。
(4)如图6,设M1,为A1A2边上的任意一点,如图6,在各边上分别截取A2M2=A3M3=A4M4=A5M5=A1M1,连结OM1、OM2、OM3、OM4、OM5,即可得到5条小路。因此可知能推广到正n边形。
四、
11、由图7可知 ∠AFC对ABC,因为 AD= CF,而∠DAF对的DEF=DBC+CF=AD+DBC=ABC,所以∠AFC=∠DAF,同理可证其余各角相等,所以图6中的六边形各内角相等。
(2)因为∠A对 BEG,∠B对CEA,且∠A=∠B,所以 BEG= CEA,所以BC=AG,同理可得
AB= CD= EF= AG= BC= DE =FG,所以其边形ABCDEFG是正七边形。
(3)猜想:当边数为奇数时,各内角相等的圆内接多边形是正多边形。
24.4答案:
一、
1、B。2、D。3、C。4、B。5、B。
二、
6、942。7、=。8、2π-2。9、3。10、相等。
三、
11、解:由题意知弯道长:LBC=LAD=2× HYPERLINK "http://www./Index.html" EMBED Equation.3 +≈101.4(m),所以跑到全长L=2AB+2LAB≈400(m),∴跑完3000米应是7圈零200米,而AB+LBC=200米固执终点应在C处。
12、解:五个圆环的覆盖部分的面积S5=5×[π()2-π()2]=45π=45×3.14=141.3。所以重叠在五个圆环上的8个小曲四边形的面积之和为S8=S5-122.5=18.8,即每个小曲四边形的面积是S8=2.35(平方单位)。
13、解:(1)=;==;==;==。
结论:每个小圆周长是大圆周长的。
设⊙O的面积为S,则S=π×()2=πa2,把AB分成两条相等的线段,每个小圆的面积S2=π×()2=πa2=S;把AB分成三条相等的线段,每个小圆的面积是S3=π×(×)2=πa2=S;把AB分成四条相等的线段,每个小圆的面积是S4=π×(×)2=πa2=S;把AB分成n条相等的线段,每个小圆的面积是Sn=π×(×)2=S;即每个小圆的面积是大圆的面积的。
20cm
30cm
图4
同课章节目录
