(试题4)24.3~24.4综合测试
文档属性
| 名称 | (试题4)24.3~24.4综合测试 |

|
|
| 格式 | zip | ||
| 文件大小 | 204.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-20 00:00:00 | ||
图片预览

文档简介
九年级上册第24.3-24.4水平测试题
一、选择题
1.已知正三角形外接圆半径为,这个正三角形的边长是( )
A. B. C. D.
2.等边三角形的外接圆的面积是内切圆面积的( )
A.2倍 B.3倍 C.4倍 D.5倍
3.如图1,一块含有30 角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到 A’B’C’的位置。若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为( )
A.cm B.cm C.cm D.cm
4.如图2,的边长都大于2,分别以它的顶点为圆心,1为半径画弧(弧的端点分别在三角形的相邻两边上),则这三条弧的长的和是( )
A. B. C. D.
5.如图3,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( )
A.S1 =S2 B.S1 <S2 C.S1>S2 D.无法确定
6.(北京)将如右图所示的圆心角为90°的扇形纸片AOB围成圆锥形纸帽,使扇形的两条
半径OA与OB重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是( )
7.如图4,小丽要制作一个圆锥模型,要求圆锥的母线长为9cm,底面圆的直径为10cm,那么小丽要制作的这个圆锥的侧面展开扇形的纸片的圆心角度数是( )
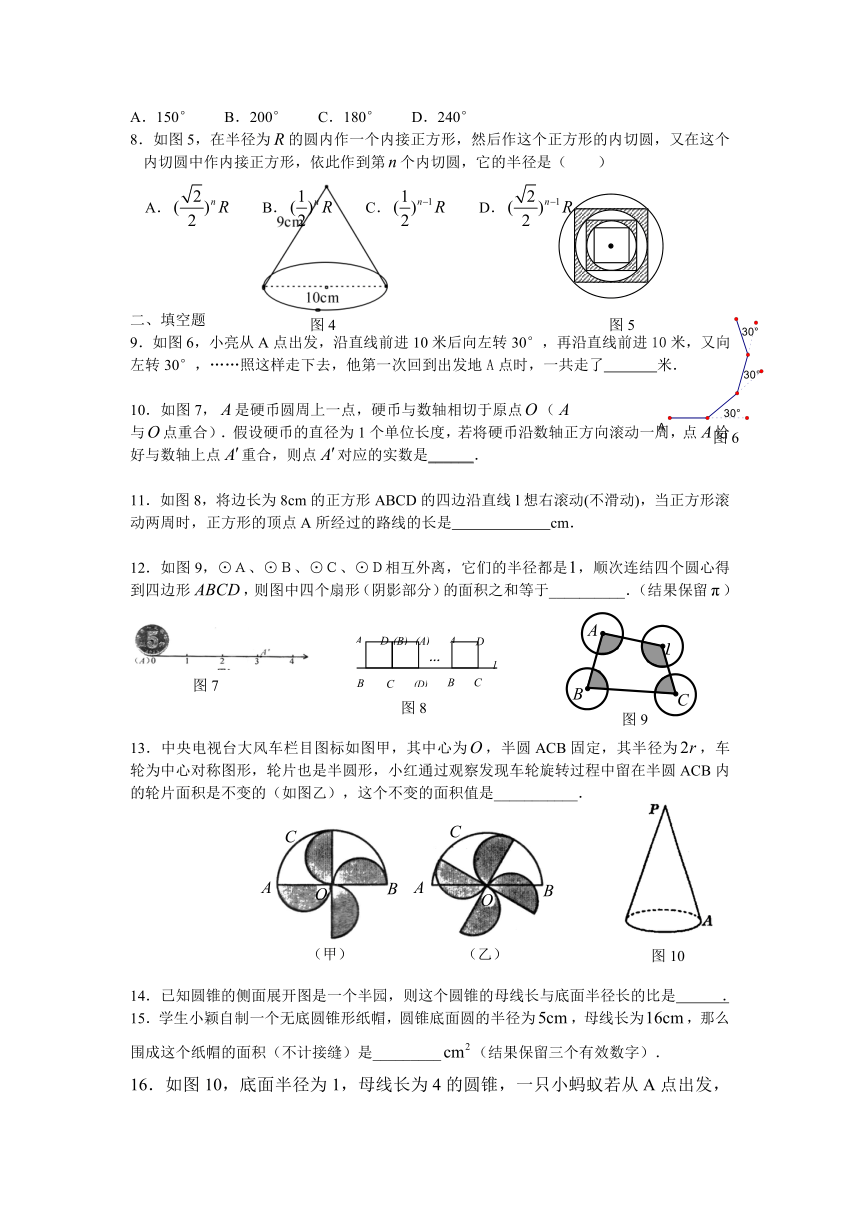
A.150° B.200° C.180° D.240°
8.如图5,在半径为的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第个内切圆,它的半径是( )
A. B. C. D.
二、填空题
9.如图6,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,……照这样走下去,他第一次回到出发地A点时,一共走了 米.
10.如图7,是硬币圆周上一点,硬币与数轴相切于原点(
与点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点恰
好与数轴上点重合,则点对应的实数是______.
11.如图8,将边长为8cm的正方形ABCD的四边沿直线l想右滚动(不滑动),当正方形滚
动两周时,正方形的顶点A所经过的路线的长是 cm.
12.如图9,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是,顺次连结四个圆心得到四边形,则图中四个扇形(阴影部分)的面积之和等于__________.(结果保留)
13.中央电视台大风车栏目图标如图甲,其中心为,半圆ACB固定,其半径为,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆ACB内的轮片面积是不变的(如图乙),这个不变的面积值是___________.
14.已知圆锥的侧面展开图是一个半园,则这个圆锥的母线长与底面半径长的比是 .
15.学生小颖自制一个无底圆锥形纸帽,圆锥底面圆的半径为,母线长为,那么
围成这个纸帽的面积(不计接缝)是_________(结果保留三个有效数字).
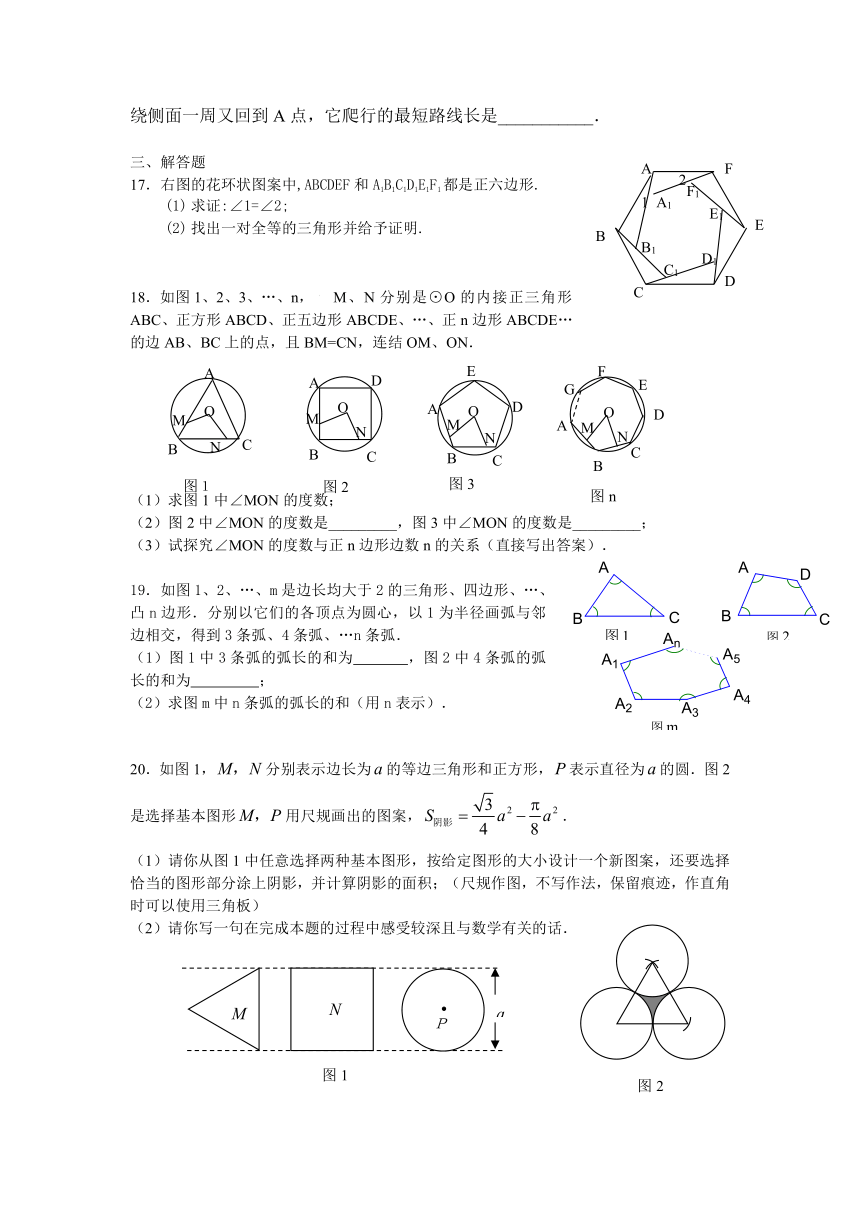
16.如图10,底面半径为1,母线长为4的圆锥,一只小蚂蚁若从A点出发,绕侧面一周又回到A点,它爬行的最短路线长是___________.
三、解答题
17.右图的花环状图案中,ABCDEF和A1B1C1D1E1F1都是正六边形.
求证:∠1=∠2;
找出一对全等的三角形并给予证明.
18.如图1、2、3、…、n,M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连结OM、ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是_________,图3中∠MON的度数是_________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
19.如图1、2、…、m是边长均大于2的三角形、四边形、…、凸n边形.分别以它们的各顶点为圆心,以1为半径画弧与邻边相交,得到3条弧、4条弧、…n条弧.
(1)图1中3条弧的弧长的和为 ,图2中4条弧的弧长的和为 ;
(2)求图m中n条弧的弧长的和(用n表示).
20.如图1,分别表示边长为的等边三角形和正方形,表示直径为的圆.图2是选择基本图形用尺规画出的图案,.
(1)请你从图1中任意选择两种基本图形,按给定图形的大小设计一个新图案,还要选择恰当的图形部分涂上阴影,并计算阴影的面积;(尺规作图,不写作法,保留痕迹,作直角时可以使用三角板)
(2)请你写一句在完成本题的过程中感受较深且与数学有关的话.
21.如图是两个半圆,点为大半圆的圆心,是大半圆的弦关与小半圆相切,且.问:能求出阴影部分的面积吗?若能,求出此面积;若不能,试说明理由.
22.某校编排的一个舞蹈需要五把和图①形状完全相同的绸扇。学校现有三把符合要求的绸
扇,将这三把绸扇完全展开刚好组成图②所示的一朵圆形的花。请你算一算:再做两把这样
的绸扇至少需要多少平方米的绸布?(单面制作,不考虑绸扇的折皱,结果用含π的式子表
示)
23.(吉林)如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC
(2)求SA∶SB.
24.如图,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB =,高BC =,求这个零件的表面积;(结果保留)
参考答案:
1-4. BCDD 5-8. ABBA 9.120
10. 11. 12. 13. 14.2:1 15.251 16.
17.(1)多边形ABCDEF与A1B1C1D1E1F1都是正六边形,所以∠1+∠A1AF=120°,∠2+A1AF=∠B1A1F1=120°,所以∠1+A1AF=∠2+∠A1AF,即∠1=∠2;(2)△ABB1≌△FAA1.因为∠F1A1B1=∠A1B1C1=120°,所以∠AB1B=∠FA1A=60°,又AB=FA,∠1=∠2,所以△ABB1≌△FAA1.
18.(1)连接OB、OC
∵ 等边△ABC内接于⊙O, ∴ ∠OBM=∠OCN=30°,∠BOC=30°
∵ BM=CN,OB=OC ∴ △OBM≌△OCN
∴∠BOM=∠CON ∴ ∠MON=∠BOC=120°
(2)同理可求得图1-2中∠MON的度数是90°;图1-3中∠MON的度数是72°.
(3)归纳上面三个图中∠MON的度数正n边形边数n的关系规律可得∠MON= HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 .
19.(1)=;=.(2)∵凸四边形的内角和为(n-2)180°,而n条弧的弧长的和恰为 HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 =个以某定点为圆心,以1为半径的圆的周长. n条弧的弧长的和为=.
20.(1)略;(2)参考举例:①运用圆的半径,可以作正方形的边上的中点,这对于作图很
有利.②这三个图形关系很密切,能组合设计许多美丽的图案,来装饰我们的生活.③数学
作图中要一丝不苟,否则产生的作图误差会影响图形的美观.
21.能(或能求出阴影部分的面积).设大圆与小圆的半径分别为,
可得,.
22.三把绸扇完全展开刚好组成一个圆
S大扇形==300,S小扇形==48,
S绸扇=300-48=252
二把绸扇所需绸布面积2×S绸扇=2×252=504
23.(1);(2),,
24.这个零件的底面积 =,这个零件的表面积 =
圆锥母线长OB =,这个零件的内侧面积 =
∴这个零件的表面积为:
附加题:
将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余);
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
按上述分割方法进行下去……
(1)请你在下图中画出第一次分割的示意图;
(2)若原正六边形的面积为,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
分割次数(n) 1 2 3 ……
正六边形的面积S
(3)观察所填表格,并结合操作,请你猜想:分割后所得的正六边形的面积S与分割次数有何关系?(S用含和n的代数式表示,不需要写出推理过程).
参考答案:
(1)如图:
(2)
分割次数(n) 1 2 3 ……
正六边形得面积S ……
(3)
图3
图2
图1
O
B
A
图5
图4
图6
图9
A
B
C
(B)
D
A
B
C
(D)
…
(A)
D
l
图8
图7
图10
(甲)
(乙)
A1
A
B
C
D
E
F
2
B1
C1
D1
E1
F1
1
A
B
C
D
O
M
N
E
F
G
图n
A
B
C
D
O
M
N
E
图3
A
C
B
M
N
O
图1
A
B
C
D
O
M
N
图2
图1
图2
图m
图2
图1
P
第22题图
图①
图②
2
y
O
4
6
8
10
x
A
A
A
B
B
B
B
B
C
M
一、选择题
1.已知正三角形外接圆半径为,这个正三角形的边长是( )
A. B. C. D.
2.等边三角形的外接圆的面积是内切圆面积的( )
A.2倍 B.3倍 C.4倍 D.5倍
3.如图1,一块含有30 角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到 A’B’C’的位置。若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为( )
A.cm B.cm C.cm D.cm
4.如图2,的边长都大于2,分别以它的顶点为圆心,1为半径画弧(弧的端点分别在三角形的相邻两边上),则这三条弧的长的和是( )
A. B. C. D.
5.如图3,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( )
A.S1 =S2 B.S1 <S2 C.S1>S2 D.无法确定
6.(北京)将如右图所示的圆心角为90°的扇形纸片AOB围成圆锥形纸帽,使扇形的两条
半径OA与OB重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是( )
7.如图4,小丽要制作一个圆锥模型,要求圆锥的母线长为9cm,底面圆的直径为10cm,那么小丽要制作的这个圆锥的侧面展开扇形的纸片的圆心角度数是( )
A.150° B.200° C.180° D.240°
8.如图5,在半径为的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第个内切圆,它的半径是( )
A. B. C. D.
二、填空题
9.如图6,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,……照这样走下去,他第一次回到出发地A点时,一共走了 米.
10.如图7,是硬币圆周上一点,硬币与数轴相切于原点(
与点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点恰
好与数轴上点重合,则点对应的实数是______.
11.如图8,将边长为8cm的正方形ABCD的四边沿直线l想右滚动(不滑动),当正方形滚
动两周时,正方形的顶点A所经过的路线的长是 cm.
12.如图9,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是,顺次连结四个圆心得到四边形,则图中四个扇形(阴影部分)的面积之和等于__________.(结果保留)
13.中央电视台大风车栏目图标如图甲,其中心为,半圆ACB固定,其半径为,车轮为中心对称图形,轮片也是半圆形,小红通过观察发现车轮旋转过程中留在半圆ACB内的轮片面积是不变的(如图乙),这个不变的面积值是___________.
14.已知圆锥的侧面展开图是一个半园,则这个圆锥的母线长与底面半径长的比是 .
15.学生小颖自制一个无底圆锥形纸帽,圆锥底面圆的半径为,母线长为,那么
围成这个纸帽的面积(不计接缝)是_________(结果保留三个有效数字).
16.如图10,底面半径为1,母线长为4的圆锥,一只小蚂蚁若从A点出发,绕侧面一周又回到A点,它爬行的最短路线长是___________.
三、解答题
17.右图的花环状图案中,ABCDEF和A1B1C1D1E1F1都是正六边形.
求证:∠1=∠2;
找出一对全等的三角形并给予证明.
18.如图1、2、3、…、n,M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连结OM、ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是_________,图3中∠MON的度数是_________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
19.如图1、2、…、m是边长均大于2的三角形、四边形、…、凸n边形.分别以它们的各顶点为圆心,以1为半径画弧与邻边相交,得到3条弧、4条弧、…n条弧.
(1)图1中3条弧的弧长的和为 ,图2中4条弧的弧长的和为 ;
(2)求图m中n条弧的弧长的和(用n表示).
20.如图1,分别表示边长为的等边三角形和正方形,表示直径为的圆.图2是选择基本图形用尺规画出的图案,.
(1)请你从图1中任意选择两种基本图形,按给定图形的大小设计一个新图案,还要选择恰当的图形部分涂上阴影,并计算阴影的面积;(尺规作图,不写作法,保留痕迹,作直角时可以使用三角板)
(2)请你写一句在完成本题的过程中感受较深且与数学有关的话.
21.如图是两个半圆,点为大半圆的圆心,是大半圆的弦关与小半圆相切,且.问:能求出阴影部分的面积吗?若能,求出此面积;若不能,试说明理由.
22.某校编排的一个舞蹈需要五把和图①形状完全相同的绸扇。学校现有三把符合要求的绸
扇,将这三把绸扇完全展开刚好组成图②所示的一朵圆形的花。请你算一算:再做两把这样
的绸扇至少需要多少平方米的绸布?(单面制作,不考虑绸扇的折皱,结果用含π的式子表
示)
23.(吉林)如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC
(2)求SA∶SB.
24.如图,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB =,高BC =,求这个零件的表面积;(结果保留)
参考答案:
1-4. BCDD 5-8. ABBA 9.120
10. 11. 12. 13. 14.2:1 15.251 16.
17.(1)多边形ABCDEF与A1B1C1D1E1F1都是正六边形,所以∠1+∠A1AF=120°,∠2+A1AF=∠B1A1F1=120°,所以∠1+A1AF=∠2+∠A1AF,即∠1=∠2;(2)△ABB1≌△FAA1.因为∠F1A1B1=∠A1B1C1=120°,所以∠AB1B=∠FA1A=60°,又AB=FA,∠1=∠2,所以△ABB1≌△FAA1.
18.(1)连接OB、OC
∵ 等边△ABC内接于⊙O, ∴ ∠OBM=∠OCN=30°,∠BOC=30°
∵ BM=CN,OB=OC ∴ △OBM≌△OCN
∴∠BOM=∠CON ∴ ∠MON=∠BOC=120°
(2)同理可求得图1-2中∠MON的度数是90°;图1-3中∠MON的度数是72°.
(3)归纳上面三个图中∠MON的度数正n边形边数n的关系规律可得∠MON= HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 .
19.(1)=;=.(2)∵凸四边形的内角和为(n-2)180°,而n条弧的弧长的和恰为 HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4 =个以某定点为圆心,以1为半径的圆的周长. n条弧的弧长的和为=.
20.(1)略;(2)参考举例:①运用圆的半径,可以作正方形的边上的中点,这对于作图很
有利.②这三个图形关系很密切,能组合设计许多美丽的图案,来装饰我们的生活.③数学
作图中要一丝不苟,否则产生的作图误差会影响图形的美观.
21.能(或能求出阴影部分的面积).设大圆与小圆的半径分别为,
可得,.
22.三把绸扇完全展开刚好组成一个圆
S大扇形==300,S小扇形==48,
S绸扇=300-48=252
二把绸扇所需绸布面积2×S绸扇=2×252=504
23.(1);(2),,
24.这个零件的底面积 =,这个零件的表面积 =
圆锥母线长OB =,这个零件的内侧面积 =
∴这个零件的表面积为:
附加题:
将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余);
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形在分割成一个正六边形和两个全等的正三角形;
按上述分割方法进行下去……
(1)请你在下图中画出第一次分割的示意图;
(2)若原正六边形的面积为,请你通过操作和观察,将第1次,第2次,第3次分割后所得的正六边形的面积填入下表:
分割次数(n) 1 2 3 ……
正六边形的面积S
(3)观察所填表格,并结合操作,请你猜想:分割后所得的正六边形的面积S与分割次数有何关系?(S用含和n的代数式表示,不需要写出推理过程).
参考答案:
(1)如图:
(2)
分割次数(n) 1 2 3 ……
正六边形得面积S ……
(3)
图3
图2
图1
O
B
A
图5
图4
图6
图9
A
B
C
(B)
D
A
B
C
(D)
…
(A)
D
l
图8
图7
图10
(甲)
(乙)
A1
A
B
C
D
E
F
2
B1
C1
D1
E1
F1
1
A
B
C
D
O
M
N
E
F
G
图n
A
B
C
D
O
M
N
E
图3
A
C
B
M
N
O
图1
A
B
C
D
O
M
N
图2
图1
图2
图m
图2
图1
P
第22题图
图①
图②
2
y
O
4
6
8
10
x
A
A
A
B
B
B
B
B
C
M
同课章节目录
