指数函数(第1课时)

(共25张PPT)
主讲人：赵茜
指数函数
湖北省大冶二中
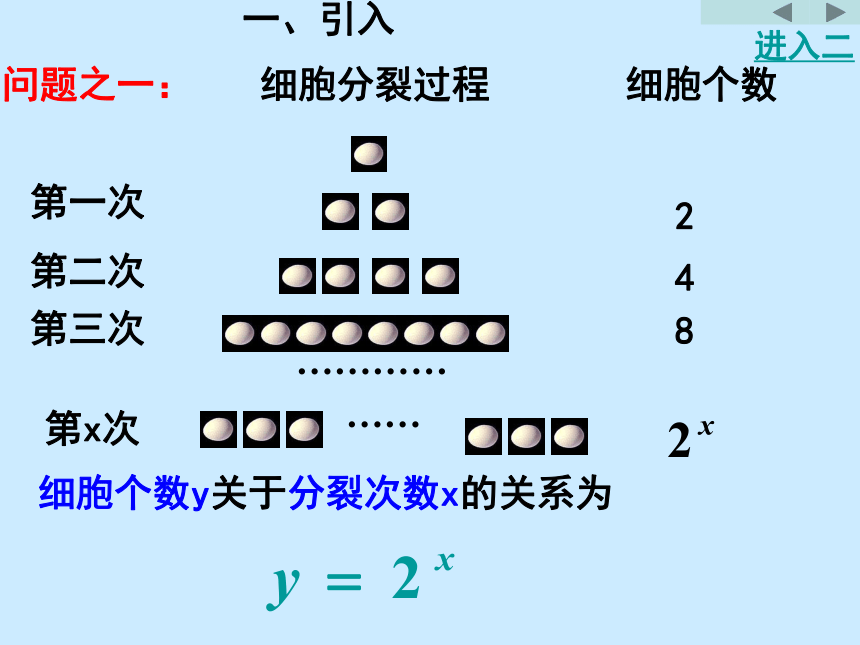
细胞分裂过程
细胞个数
第一次
第二次
第三次
2
8
4
…………
第x次
……
细胞个数y关于分裂次数x的关系为
一、引入
问题之一：
进入二
　一把长为1尺子第1次截去它的一半,第2次截去剩余部分的一半，第3次截去第2次剩余部分的一半， ······ ，依次截下去,问截的次数x与剩下的尺子长度y之间的关系.
　　
问题之二：半中折半
进入二
次数 长度
1次
2次
3次
4次
…
…
我们可以看到每截一次后尺的长度都减为前一次的二分之一倍，一把尺子截x次后，得到的尺子的长度y与x的函数关系式是
x次
进入二
在
,
中指数x是自变量，
底数是一个大于0且不等于1的常量.
我们把这种自变量在指数位置上而底数是一
个大于0且不等于1的常数的函数叫做指数函数.
对指数函数认识 以及相关的性质就是本课要学习和研讨的主要内容
指数函数（第一课）
进入二
指数函数的定义：
函数
其中x是自变量，函数定义域是R。
思考(3) ：函数 y=2·3x 是指数函数吗？
探究1：讨论a的活动范围 (为什么要规定a>0,且a≠1呢？)
反馈练习1 ：下列函数中，那些是指数函数？
(1) (3) (9)
(1) y=3x
(7) y= -3x
(4) y=(-3)x
(3)y=πx
(5) y=3x3
(8) y=xx
(9) y=(3a-1)x(a>1/3且a≠2/3)
(2) y=x3
(6) y=33x+1
二、指数函数定义
叫做指数函数，
进入三
要使教材中y＝a x 的x∈R，请思考:
(1)a=0 能恒成立吗 如不能,则请举一反例说明.
(2)a<0 能恒成立吗
(3)a>0 能恒成立吗 如能,那还怎样需进一步分
类讨论呢
探究1：讨论a的活动范围
(为什么要规定a>0,且a≠1呢？)
a>1
0本课研讨的对象.
a=1 即y=1 常值函数.
返回定义
则当x>0时，
=0；
无意义.
当x≤0时，
则对于x的某些数值，
可能无意义.
如
，这时对于x=
，x=
……等等，在实数范围内函数值不存在.
则对于任何
X∈R，
=1，是一个常量，没有研究的必要性.
在规定以后，对于任何
x∈R，
都有意义，
因此指数函数的定义域是R，值域是(0,+∞).
返回定义
为了避免上述各种情况，所以规定a>0且a 1。
②若a<0，
③若a=1，
①若a=0，
反思：函数 y=2·3x 是指数函数吗？
指数函数的解析式 y=
中，
的系数是1.
有些函数貌似指数函数，实际上却不是，
如:
( a>0 且 a
1，k
Z)；
有些函数看起来不像指数函数，实际上却是，
如:
因为它可以化为
返回定义
三、指数函数的图象和性质
例题：在同一坐标系中分别作出如下函数的图像：
⑴列表 ⑵描点 ⑶连线
探究2：以上图象有哪些特征？
由此得出图像有哪些性质？ (定义域、值域、过定点、单调性)
性质回顾
进入四
二
(1)列表
x … -3 -2 -1 -0.5 0 0.5 1 2 3 …
… …
… …
x … -1.5 -1 -0.5 -0.25 0 0.25 0.5 1 1.5 …
… …
… …
返回三
x … -3 -2 -1 -0.5 0 0.5 1 2 3 …
… 0.125 0.25 0.5 0.71 1 1.4 2 4 8 …
… 8 4 2 1.4 1 0.71 0.5 0.25 0.125 …
x … -1.5 -1 -0.5 -0.25 0 0.25 0.5 1 1.5 …
… 0.03 0.1 0.32 0.56 1 1.78 3.16 10 31.62 …
… 31.62 10 3.16 1.78 1 0.56 0.32 0.1 0.03 …
(1)列表
返回三
(2)描点 连线
返回三
返回性质
图象和性质：
a>1 0图
象
性
质 1.定义域：
2.值域：
3.过点 ，即x= 时，y=
4.在 R上是 函数 在R上是 函数
返回图像
返回三
四、指数函数图象和性质的应用
进入五
三
例1 求下列函数的定义域和值域:
解（1）由指数函数的性质可知，
（2）由题意，要使得函数有意义，则
所以函数定义域为：
又由指数函数性质可知值域为：
所以函数定义域为：
令
所以原函数的值域为：
例2：看图说出下列各题中两个值的大小：
解：
① ∵函数y=1.7x
在R上是增函数，
；
(1)1.72.5__ 1.73
(3)1.70.5__ 0.82.5
(2)0.8—1__0.8--2
∴1.72.5 < 1.73
又∵ 2.5 < 3 ，
返四
② ∵函数y=0.8x
在R上是减函数，
∴ 0.8—1 < 0.8 — 2
又∵ -1 > -2 ，
(2)0.8—1__0.8--2
返四
；
∴1.70.5 > 0.82.5
③ ∵ 1.7 0.5 > 1.70 = 1
= 0.80 >0.8 2.5 ，
(3)1.70.5__ 0.82.5
返四
函数
叫做指数函数，其中x是自变量，函数定义域是R。
指数函数的定义：
a>1 0图
象
性
质 1.定义域：R
2.值域：（0，+∞）
3.过点（0，1），即x=0时，y=1
4.在 R上是增函数 在R上是减函数
指数函数的图象和性质：
五、归纳小结：
返四
进六
对同底数不同指数的幂大小的比较用的是指数函数的单调性, 如： 0.75-0.1>0.752 , 308 > 307 ;
返五
对不同底数，不同指数的幂的大小的比较可以与
中间值1进行比较, 如： 1.70.5>1.70 =1= 0.80 >0.82.5 。
练习:
1.比较下列各组数的大小
书面作业
课本 P73.练习1，
习题2.6 2 (3),(4) ; 3(3),(4)
非书面作业
1理解记忆指数函数的图象与性质.
2复习本课所讲例题.
七、课后作业：
谢谢大家!