人教版数学八年级上册 13.3等腰三角形同步测试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 13.3等腰三角形同步测试题(一)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 198.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 09:11:45 | ||
图片预览


文档简介
等腰三角形同步测试题(一)
一.选择题
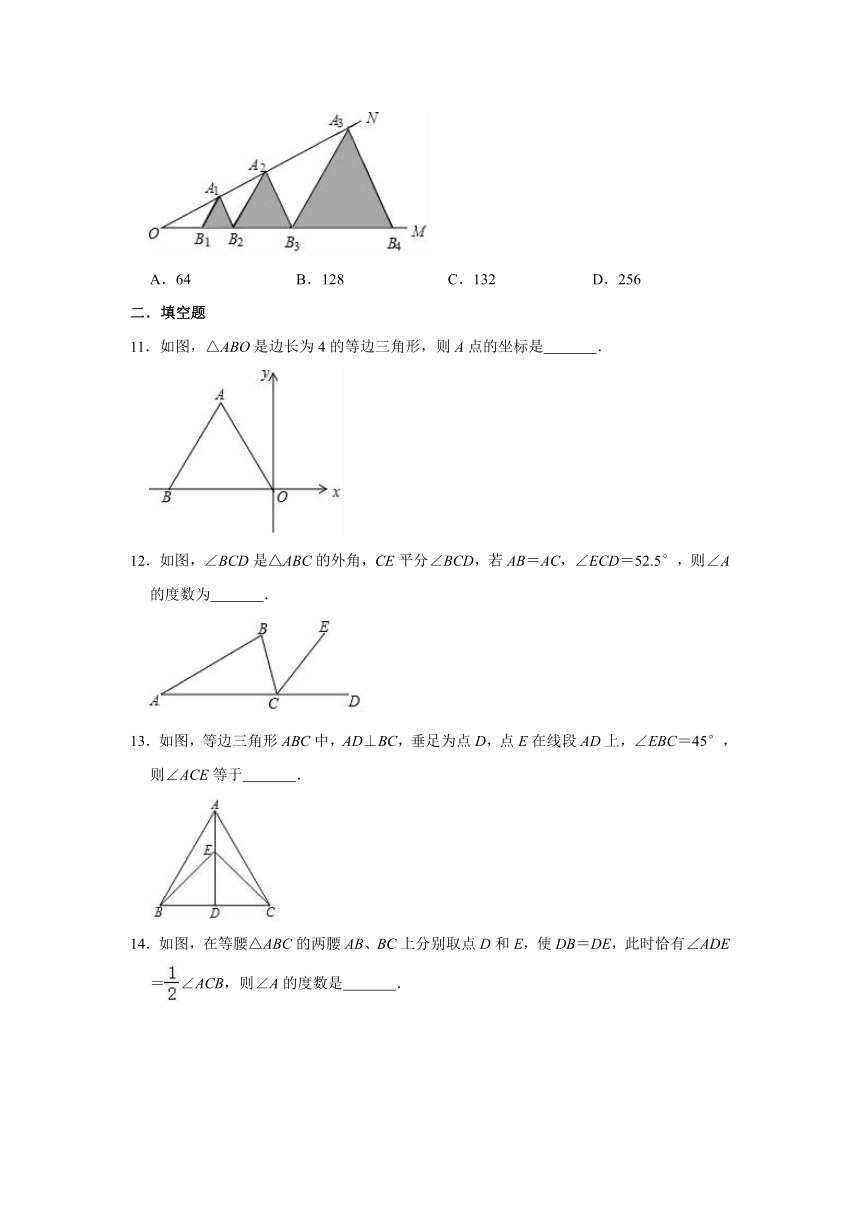
1.如图,在△ABC中,CB=AC,DE垂直平分AC,垂足为E,交BC于点D,若∠B=70°,则∠BAD=( )
A.30°
B.40°
C.50°
D.60°
2.如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E使CE=CD,则图中等腰三角形的个数是( )
A.1个
B.2个
C.3个
D.4个
3.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为( )
A.30°
B.34°
C.36°
D.40°
4.如图,△ABC中,AB=AC,过点A作DA⊥AC交BC于点D.若∠B=2∠BAD,则∠BAD的度数为( )
A.18°
B.20°
C.30°
D.36°
5.如图,在△ABC中,AB=AC,∠A=40°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D=( )
A.18°
B.20°
C.22°
D.25°
6.等腰三角形的两边长为6cm和8cm,则它的周长为( )
A.20cm
B.22cm
C.20cm或22cm
D.18cm、20cm或22cm
7.如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为16,BC=7,则AB的长为( )
A.8
B.9
C.10
D.11
8.已知等腰三角形ABC的底边BC=8,且|AC﹣BC|=4,则腰AC长为( )
A.4或12
B.12
C.4
D.8或12
9.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.图中等腰三角形的个数为( )
A.4
B.3
C.2
D.1
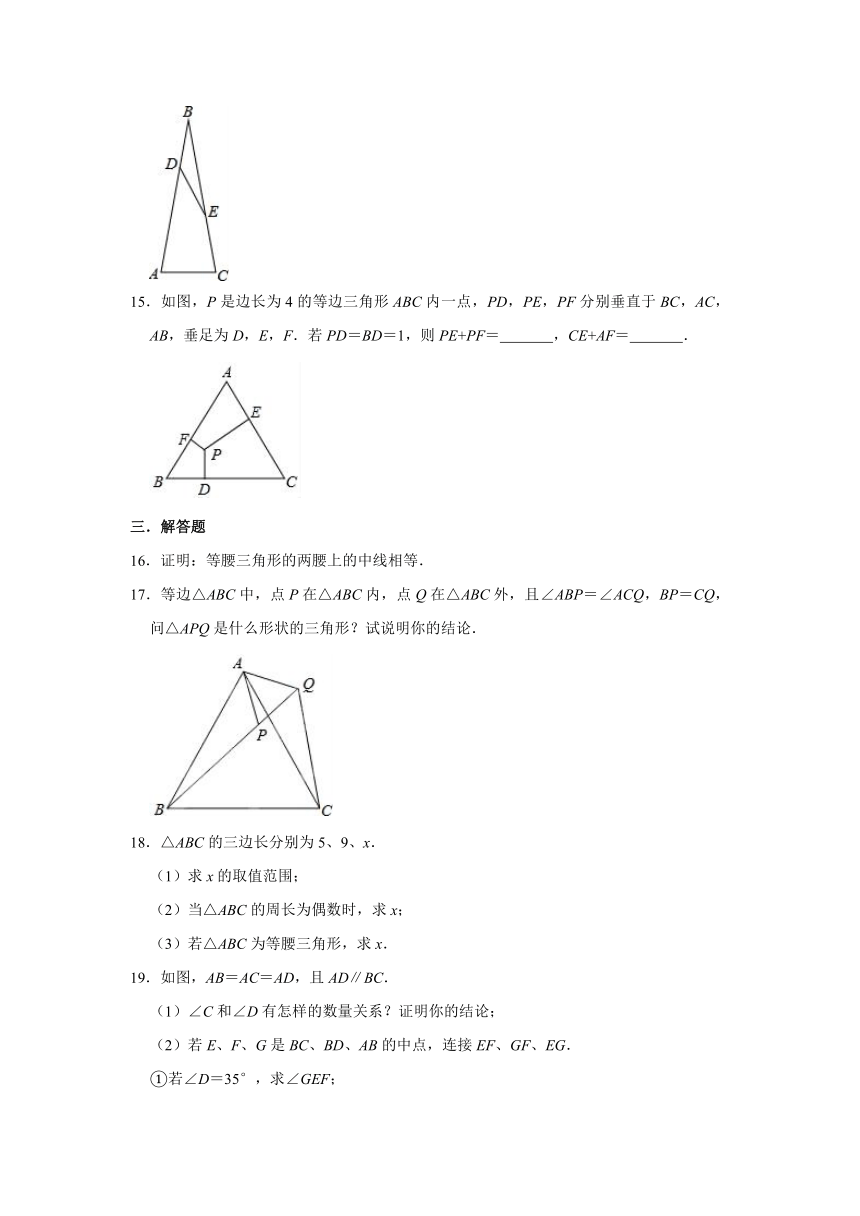
10.如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1B2,△A2B2B3,△A3B3B4,…均为等边三角形.若OB1=1,则△A8B8B9的边长为( )
A.64
B.128
C.132
D.256
二.填空题
11.如图,△ABO是边长为4的等边三角形,则A点的坐标是
.
12.如图,∠BCD是△ABC的外角,CE平分∠BCD,若AB=AC,∠ECD=52.5°,则∠A的度数为
.
13.如图,等边三角形ABC中,AD⊥BC,垂足为点D,点E在线段AD上,∠EBC=45°,则∠ACE等于
.
14.如图,在等腰△ABC的两腰AB、BC上分别取点D和E,使DB=DE,此时恰有∠ADE=∠ACB,则∠A的度数是
.
15.如图,P是边长为4的等边三角形ABC内一点,PD,PE,PF分别垂直于BC,AC,AB,垂足为D,E,F.若PD=BD=1,则PE+PF=
,CE+AF=
.
三.解答题
16.证明:等腰三角形的两腰上的中线相等.
17.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
18.△ABC的三边长分别为5、9、x.
(1)求x的取值范围;
(2)当△ABC的周长为偶数时,求x;
(3)若△ABC为等腰三角形,求x.
19.如图,AB=AC=AD,且AD∥BC.
(1)∠C和∠D有怎样的数量关系?证明你的结论;
(2)若E、F、G是BC、BD、AB的中点,连接EF、GF、EG.
①若∠D=35°,求∠GEF;
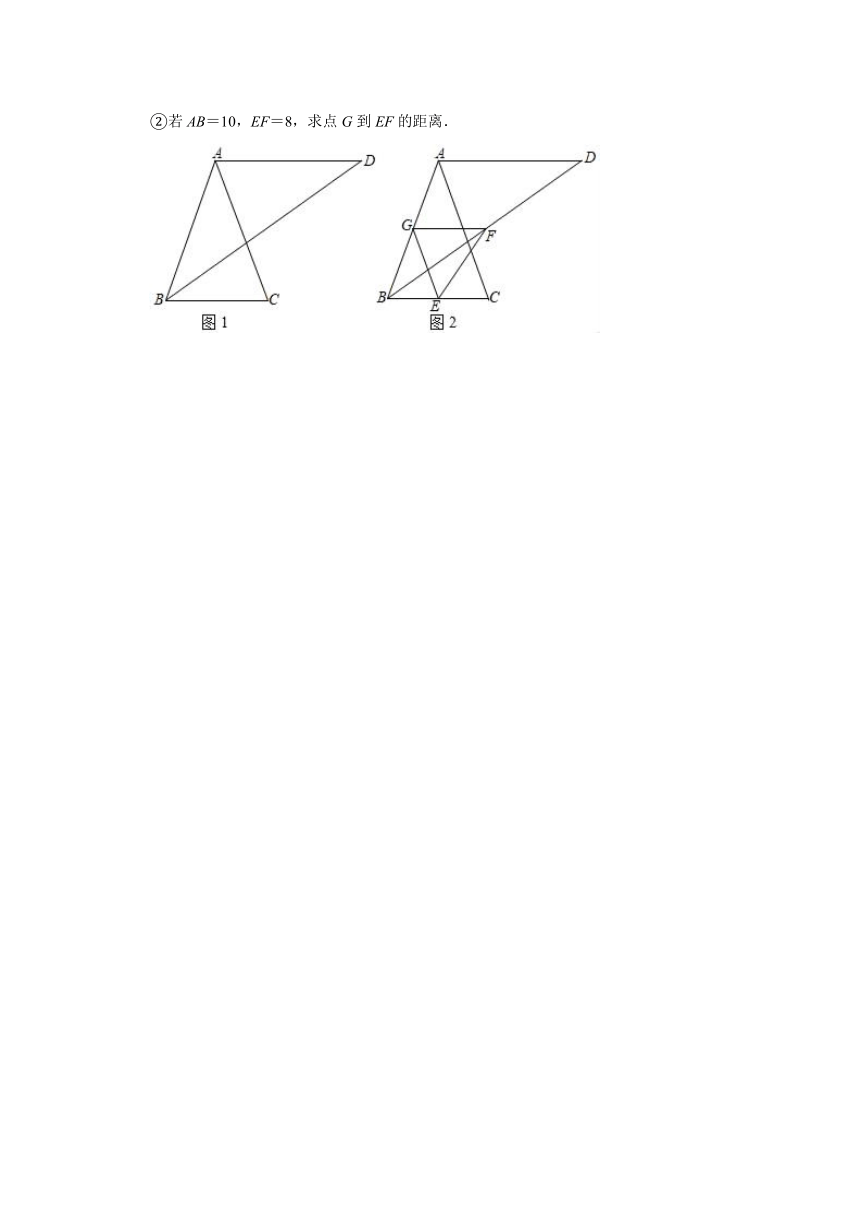
②若AB=10,EF=8,求点G到EF的距离.
参考答案与试题解析
一.选择题
1.【解答】解:∵CB=CA,
∴∠B=∠BAC=70°,
∴∠C=180°﹣70°﹣70°=40°,
∵DE垂直平分AC,
∴∠DAC=∠C=40°,
∴∠BAD=30°,
故选:A.
2.【解答】解:∵CD=CE,
∴∠E=∠EDC,
∴CE=CD,
∴△EDC是等腰三角形;
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠E=30°,
∵△ABC是等边三角形,BD是高,
∴∠DBC=30°,
∴∠E=∠DBC,
∴DB=DE,
∴△BDE是等腰三角形,
故选:C.
3.【解答】解:∵AB=BD,∠B=40°,
∴∠ADB=70°,
∵∠C=36°,
∴∠DAC=∠ADB﹣∠C=34°.
故选:B.
4.【解答】解:∵AB=AC,
∴∠B=∠C,
∵DA⊥AC,
∴∠DAC=90°,
∴∠ADC=90°﹣∠C=90°﹣∠B=∠BAD+∠B,
∵∠B=2∠BAD,
∴4∠BAD=90°﹣∠BAD,
∴∠BAD=18°,
故选:A.
5.【解答】解:∵∠ABC的平分线与∠ACE的平分线交于点D,
∴∠1=∠2,∠3=∠4,
∵∠ACE=∠A+∠ABC,
即∠1+∠2=∠3+∠4+∠A,
∴2∠1=2∠3+∠A,
∵∠1=∠3+∠D,
∴∠D=∠A=×40°=20°.
故选:B.
6.【解答】解:当三边是8cm,8cm,6cm时,符合三角形的三边关系,此时周长是22cm;
当三边是8cm,6cm,6cm时,符合三角形的三边关系,此时周长是20cm.
因此等腰三角形的周长为22cm或20cm.
故选:C.
7.【解答】解:由已知得,BC+BE+CE=16,
∵BC=7,
∴BE+CE=9,
∵DE垂直平分AB,
∴AE=BE,
∴AE+CE=9,
即AC=9,
∵AB=AC,
∴AB=9.
故选:B.
8.【解答】解:∵|AC﹣BC|=4,
∴AC﹣BC=±4,
∵等腰△ABC的底边BC=8,
∴AC=12.AC=4(不合题意舍去),
故选:B.
9.【解答】解:∵BF是∠ABC的平分线,
∴∠1=∠2,
∵CF是∠ACB的平分线,
∴∠3=∠4,
∵DE∥BC,
∴∠2=∠5,∠4=∠6,
∴∠1=∠5,∠3=∠6,
∴BD=DF,EF=EC,
∴△BDF和△CEF是等腰三角形.
故选:C.
10.【解答】解:∵△A1B1B2是等边三角形,
∴∠A1B1B2=∠A1B2O=60°,A1B1=A1B2,
∵∠O=30°,
∴∠A2A1B2=∠O+∠A1B2O=90°,
∵∠A1B1B2=∠O+∠OA1B1,
∴∠O=∠OA1B1=30°,
∴OB1=A1B1=A1B2=1,
在Rt△A2A1B2中,∵∠A1A2B2=30°
∴A2B2=2A1B2=2,
同法可得A3B3=22,A4B4=23,…,AnBn=2n﹣1,
∴△A8B8B9的边长=27=128,
故选:B.
二.填空题(共5小题)
11.【解答】解:过点A作AC⊥OB于点C,
∵△AOB是等边三角形,OB=4,
∴OC=BC=2,∠OAC=∠OAB=30°,
在Rt△AOC中,
∵∠OAC=30°,OA=4,
∴OC=2,AC=OAcos30°=4×=2
∴A(﹣2,2).
故答案为:(﹣2,2).
12.【解答】解:∵CE平分∠BCD,∠ECD=52.5°,
∴∠BCD=2∠ECD=105°,
∴∠ACB=180°﹣∠BCD=180°﹣105°=75°,
∵AB=AC,
∴∠B=∠ACB=75°,
∴∠A=30°,
故答案为:30°.
13.【解答】解:∵△ABC是等边三角形,
∴∠ACB=60°,
∵AD⊥BC,
∴BD=DC,
∴EB=EC,
∴∠ECB=∠EBC=45°,
∴∠ACE=∠ACB﹣∠ECB=15°,
故答案为15°
14.【解答】解:设∠B=x.
∵DB=DE,
∴∠DEB=∠B=x,
∴∠ADE=∠DEB+∠B=2x,
∴∠ACB=2∠ADE=4x.
∵AB=BC,
∴∠ACB=∠A=4x.
在△ABC中,∵∠A+∠B+∠C=180°,
∴4x+x+4x=180°,
∴x=20°.
即∠B=20°
∴∠A=4x=80°
故答案为:80°
15.【解答】解:过A作AG⊥BC于G,
∵△ABC是等边三角形,
∴CG=BC=2,
∴AG=2,
连接PA、PB、PC,
∵PD,PE,PF分别垂直于BC,AC,AB,
∴S△ABC=S△APB+S△PBC+S△APC,
+,
AB=AB(PE+1+PF),
∴PE+PF=2﹣1,
延长DP交AB于H,
∵PF⊥AB,PD⊥BC,
∴∠BFP=∠BDP=90°,
∵∠ABC=60°,
∴∠HFP=60°,
∴∠BHD=30°,
∵BD=1,
∴BH=2,DH=,
∵PD=1,
∴PH=﹣1,
Rt△PFH中,PF=,
∴FH==,
∴BF=BH﹣FH=2﹣=,
∴AF=4﹣BF=,
∵PE+PF=2﹣1,
∴PE=2﹣1﹣=,
Rt△PDC中,PC===,
∴CE====,
∴CE+AF==5
故答案为:2﹣1,5
三.解答题(共4小题)
16.【解答】已知:△ABC中,AB=AC,AD=DC,AE=EB,
求证:BD=CE.
证明:∵AB=AC,AD=DC,AE=EB,
∴DC=BE,∠DCB=∠EBC.
∵BC=CB,
∴△BDC≌△CEB(SAS).
∴BD=CE.
即等腰三角形的两腰上的中线相等.
17.【解答】解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
18.【解答】解:△ABC的三边长分别为5、9、x,
(1)根据三角形的第三边大于两边之差,而小于两边之和,得9﹣5<x<9+5,即4<x<14;
(2)∵三角形的已知两边的和等于14,△ABC的周长为偶数,
∴第三边x为偶数,
∵4<x<14,
∴x=6、8、10、12;
(3)若△ABC为等腰三角形,x=5或9.
19.【解答】(1)解:∠C=2∠D.
证明:∵AB=AD,
∴∠D=∠ABD,
∵AD∥BC,
∴∠D=∠DBC,
∴∠D=∠ABD=∠DBC,
∵AB=AC,
∴∠C=∠ABC=∠ABD+∠DBC=2∠D;
(2)解:①连接AE,AF,如图2,
∵在△ABC中,AB=AC,E为BC的中点,
∴AE⊥BC(三线合一),
同理AF⊥BD,
∴△ABE和△ABF都为直角三角形,
∵G为两直角三角形斜边的中点,
∴EG=FG=AB=GB=GA,
∴△GEF是等腰三角形,
由(1)可知∠C=2∠D=2×35°=70°,
∴∠AGE=2∠ABC=2×70°=140°,∠AGF=2∠ABD=2×35°=70°,
∴EGF=∠AGE﹣∠AGF=140°﹣70°=70°,
∴∠GEF=(180°﹣∠EGF)=55°;
②取EF的中点H,连接GH,
由①可知GE=GF,在
∴GE=AB=×10=5,EH=EF=×8=4,且GH⊥EF(三线合一),
∴GE2=EH2+GH2,
即52=42=GH2,
即点G到EF的距离为3.
一.选择题
1.如图,在△ABC中,CB=AC,DE垂直平分AC,垂足为E,交BC于点D,若∠B=70°,则∠BAD=( )
A.30°
B.40°
C.50°
D.60°
2.如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E使CE=CD,则图中等腰三角形的个数是( )
A.1个
B.2个
C.3个
D.4个
3.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为( )
A.30°
B.34°
C.36°
D.40°
4.如图,△ABC中,AB=AC,过点A作DA⊥AC交BC于点D.若∠B=2∠BAD,则∠BAD的度数为( )
A.18°
B.20°
C.30°
D.36°
5.如图,在△ABC中,AB=AC,∠A=40°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D=( )
A.18°
B.20°
C.22°
D.25°
6.等腰三角形的两边长为6cm和8cm,则它的周长为( )
A.20cm
B.22cm
C.20cm或22cm
D.18cm、20cm或22cm
7.如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为16,BC=7,则AB的长为( )
A.8
B.9
C.10
D.11
8.已知等腰三角形ABC的底边BC=8,且|AC﹣BC|=4,则腰AC长为( )
A.4或12
B.12
C.4
D.8或12
9.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.图中等腰三角形的个数为( )
A.4
B.3
C.2
D.1
10.如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1B2,△A2B2B3,△A3B3B4,…均为等边三角形.若OB1=1,则△A8B8B9的边长为( )
A.64
B.128
C.132
D.256
二.填空题
11.如图,△ABO是边长为4的等边三角形,则A点的坐标是
.
12.如图,∠BCD是△ABC的外角,CE平分∠BCD,若AB=AC,∠ECD=52.5°,则∠A的度数为
.
13.如图,等边三角形ABC中,AD⊥BC,垂足为点D,点E在线段AD上,∠EBC=45°,则∠ACE等于
.
14.如图,在等腰△ABC的两腰AB、BC上分别取点D和E,使DB=DE,此时恰有∠ADE=∠ACB,则∠A的度数是
.
15.如图,P是边长为4的等边三角形ABC内一点,PD,PE,PF分别垂直于BC,AC,AB,垂足为D,E,F.若PD=BD=1,则PE+PF=
,CE+AF=
.
三.解答题
16.证明:等腰三角形的两腰上的中线相等.
17.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
18.△ABC的三边长分别为5、9、x.
(1)求x的取值范围;
(2)当△ABC的周长为偶数时,求x;
(3)若△ABC为等腰三角形,求x.
19.如图,AB=AC=AD,且AD∥BC.
(1)∠C和∠D有怎样的数量关系?证明你的结论;
(2)若E、F、G是BC、BD、AB的中点,连接EF、GF、EG.
①若∠D=35°,求∠GEF;
②若AB=10,EF=8,求点G到EF的距离.
参考答案与试题解析
一.选择题
1.【解答】解:∵CB=CA,
∴∠B=∠BAC=70°,
∴∠C=180°﹣70°﹣70°=40°,
∵DE垂直平分AC,
∴∠DAC=∠C=40°,
∴∠BAD=30°,
故选:A.
2.【解答】解:∵CD=CE,
∴∠E=∠EDC,
∴CE=CD,
∴△EDC是等腰三角形;
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠E=30°,
∵△ABC是等边三角形,BD是高,
∴∠DBC=30°,
∴∠E=∠DBC,
∴DB=DE,
∴△BDE是等腰三角形,
故选:C.
3.【解答】解:∵AB=BD,∠B=40°,
∴∠ADB=70°,
∵∠C=36°,
∴∠DAC=∠ADB﹣∠C=34°.
故选:B.
4.【解答】解:∵AB=AC,
∴∠B=∠C,
∵DA⊥AC,
∴∠DAC=90°,
∴∠ADC=90°﹣∠C=90°﹣∠B=∠BAD+∠B,
∵∠B=2∠BAD,
∴4∠BAD=90°﹣∠BAD,
∴∠BAD=18°,
故选:A.
5.【解答】解:∵∠ABC的平分线与∠ACE的平分线交于点D,
∴∠1=∠2,∠3=∠4,
∵∠ACE=∠A+∠ABC,
即∠1+∠2=∠3+∠4+∠A,
∴2∠1=2∠3+∠A,
∵∠1=∠3+∠D,
∴∠D=∠A=×40°=20°.
故选:B.
6.【解答】解:当三边是8cm,8cm,6cm时,符合三角形的三边关系,此时周长是22cm;
当三边是8cm,6cm,6cm时,符合三角形的三边关系,此时周长是20cm.
因此等腰三角形的周长为22cm或20cm.
故选:C.
7.【解答】解:由已知得,BC+BE+CE=16,
∵BC=7,
∴BE+CE=9,
∵DE垂直平分AB,
∴AE=BE,
∴AE+CE=9,
即AC=9,
∵AB=AC,
∴AB=9.
故选:B.
8.【解答】解:∵|AC﹣BC|=4,
∴AC﹣BC=±4,
∵等腰△ABC的底边BC=8,
∴AC=12.AC=4(不合题意舍去),
故选:B.
9.【解答】解:∵BF是∠ABC的平分线,
∴∠1=∠2,
∵CF是∠ACB的平分线,
∴∠3=∠4,
∵DE∥BC,
∴∠2=∠5,∠4=∠6,
∴∠1=∠5,∠3=∠6,
∴BD=DF,EF=EC,
∴△BDF和△CEF是等腰三角形.
故选:C.
10.【解答】解:∵△A1B1B2是等边三角形,
∴∠A1B1B2=∠A1B2O=60°,A1B1=A1B2,
∵∠O=30°,
∴∠A2A1B2=∠O+∠A1B2O=90°,
∵∠A1B1B2=∠O+∠OA1B1,
∴∠O=∠OA1B1=30°,
∴OB1=A1B1=A1B2=1,
在Rt△A2A1B2中,∵∠A1A2B2=30°
∴A2B2=2A1B2=2,
同法可得A3B3=22,A4B4=23,…,AnBn=2n﹣1,
∴△A8B8B9的边长=27=128,
故选:B.
二.填空题(共5小题)
11.【解答】解:过点A作AC⊥OB于点C,
∵△AOB是等边三角形,OB=4,
∴OC=BC=2,∠OAC=∠OAB=30°,
在Rt△AOC中,
∵∠OAC=30°,OA=4,
∴OC=2,AC=OAcos30°=4×=2
∴A(﹣2,2).
故答案为:(﹣2,2).
12.【解答】解:∵CE平分∠BCD,∠ECD=52.5°,
∴∠BCD=2∠ECD=105°,
∴∠ACB=180°﹣∠BCD=180°﹣105°=75°,
∵AB=AC,
∴∠B=∠ACB=75°,
∴∠A=30°,
故答案为:30°.
13.【解答】解:∵△ABC是等边三角形,
∴∠ACB=60°,
∵AD⊥BC,
∴BD=DC,
∴EB=EC,
∴∠ECB=∠EBC=45°,
∴∠ACE=∠ACB﹣∠ECB=15°,
故答案为15°
14.【解答】解:设∠B=x.
∵DB=DE,
∴∠DEB=∠B=x,
∴∠ADE=∠DEB+∠B=2x,
∴∠ACB=2∠ADE=4x.
∵AB=BC,
∴∠ACB=∠A=4x.
在△ABC中,∵∠A+∠B+∠C=180°,
∴4x+x+4x=180°,
∴x=20°.
即∠B=20°
∴∠A=4x=80°
故答案为:80°
15.【解答】解:过A作AG⊥BC于G,
∵△ABC是等边三角形,
∴CG=BC=2,
∴AG=2,
连接PA、PB、PC,
∵PD,PE,PF分别垂直于BC,AC,AB,
∴S△ABC=S△APB+S△PBC+S△APC,
+,
AB=AB(PE+1+PF),
∴PE+PF=2﹣1,
延长DP交AB于H,
∵PF⊥AB,PD⊥BC,
∴∠BFP=∠BDP=90°,
∵∠ABC=60°,
∴∠HFP=60°,
∴∠BHD=30°,
∵BD=1,
∴BH=2,DH=,
∵PD=1,
∴PH=﹣1,
Rt△PFH中,PF=,
∴FH==,
∴BF=BH﹣FH=2﹣=,
∴AF=4﹣BF=,
∵PE+PF=2﹣1,
∴PE=2﹣1﹣=,
Rt△PDC中,PC===,
∴CE====,
∴CE+AF==5
故答案为:2﹣1,5
三.解答题(共4小题)
16.【解答】已知:△ABC中,AB=AC,AD=DC,AE=EB,
求证:BD=CE.
证明:∵AB=AC,AD=DC,AE=EB,
∴DC=BE,∠DCB=∠EBC.
∵BC=CB,
∴△BDC≌△CEB(SAS).
∴BD=CE.
即等腰三角形的两腰上的中线相等.
17.【解答】解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
18.【解答】解:△ABC的三边长分别为5、9、x,
(1)根据三角形的第三边大于两边之差,而小于两边之和,得9﹣5<x<9+5,即4<x<14;
(2)∵三角形的已知两边的和等于14,△ABC的周长为偶数,
∴第三边x为偶数,
∵4<x<14,
∴x=6、8、10、12;
(3)若△ABC为等腰三角形,x=5或9.
19.【解答】(1)解:∠C=2∠D.
证明:∵AB=AD,
∴∠D=∠ABD,
∵AD∥BC,
∴∠D=∠DBC,
∴∠D=∠ABD=∠DBC,
∵AB=AC,
∴∠C=∠ABC=∠ABD+∠DBC=2∠D;
(2)解:①连接AE,AF,如图2,
∵在△ABC中,AB=AC,E为BC的中点,
∴AE⊥BC(三线合一),
同理AF⊥BD,
∴△ABE和△ABF都为直角三角形,
∵G为两直角三角形斜边的中点,
∴EG=FG=AB=GB=GA,
∴△GEF是等腰三角形,
由(1)可知∠C=2∠D=2×35°=70°,
∴∠AGE=2∠ABC=2×70°=140°,∠AGF=2∠ABD=2×35°=70°,
∴EGF=∠AGE﹣∠AGF=140°﹣70°=70°,
∴∠GEF=(180°﹣∠EGF)=55°;
②取EF的中点H,连接GH,
由①可知GE=GF,在
∴GE=AB=×10=5,EH=EF=×8=4,且GH⊥EF(三线合一),
∴GE2=EH2+GH2,
即52=42=GH2,
即点G到EF的距离为3.
