鲁教版九年级数学上册期末复习测试题—直角三角形的边角关系(word版含解析)
文档属性
| 名称 | 鲁教版九年级数学上册期末复习测试题—直角三角形的边角关系(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 433.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 10:54:51 | ||
图片预览



文档简介
直角三角形的边角关系
测试题
一.选择题(共12小题)
1.在△ABC中,∠C=90°,若AC=3,AB=4,则( )
A.BC=5
B.sinA>tanB
C.cosA=
D.tanA=cosB
2.若sin(75°﹣θ)的值是,则θ=( )
A.15°
B.30°
C.45°
D.60°
3.计算sin230°+cos260°的结果为( )
A.
B.
C.1
D.
4.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,AB=2BC,则tan∠ABD的值为( )
A.2
B.
C.
D.
5.如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD=( )
A.
B.3
C.
D.2
6.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则tan∠AOC的值为( )
A.
B.
C.
D.
7.已知水库的拦水坝斜坡的坡度为1:,则这个拦水坝的坡角为( )度.
A.30
B.45
C.60
D.90
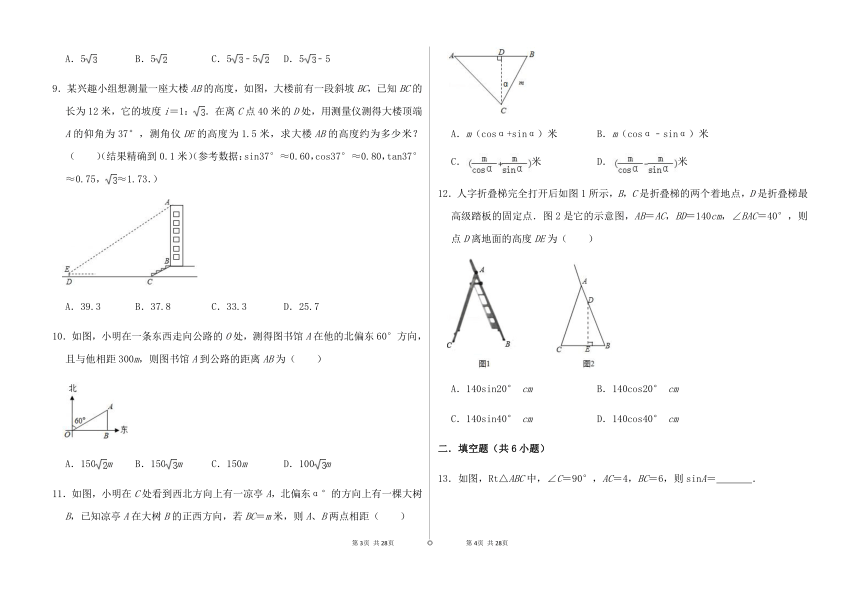
8.如图,这是某市政道路的交通指示牌,BD的距离为5m,从D点测得指示牌顶端A点和底端C点的仰角分别是60°和45°,则指示牌的高度,即AC的长度是( )m.
A.5
B.5
C.5﹣5
D.5﹣5
9.某兴趣小组想测量一座大楼AB的高度,如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:.在离C点40米的D处,用测量仪测得大楼顶端A的仰角为37°,测角仪DE的高度为1.5米,求大楼AB的高度约为多少米?( )(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73.)
A.39.3
B.37.8
C.33.3
D.25.7
10.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距300m,则图书馆A到公路的距离AB为( )
A.150m
B.150m
C.150m
D.100m
11.如图,小明在C处看到西北方向上有一凉亭A,北偏东α°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=m米,则A、B两点相距( )
A.m(cosα+sinα)米
B.m(cosα﹣sinα)米
C.米
D.米
12.人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,则点D离地面的高度DE为( )
A.140sin20°
cm
B.140cos20°
cm
C.140sin40°
cm
D.140cos40°
cm
二.填空题(共6小题)
13.如图,Rt△ABC中,∠C=90°,AC=4,BC=6,则sinA=
.
14.在△ABC中,若|sinA﹣|+(cosB﹣)2=0,则△ABC的形状是
.
15.已知:AD是△ABC的高,其中tan∠CAD=,AB=5,AC=,则tan∠BAC的值为
.
16.如图,斜面AC的坡度(CD与AD的比)为1:2,坡顶有一旗杆BC,顶端B点与A点有一条彩带相连,已知CD=3米,AB=10米,则旗杆BC的高度为
米.
17.如图,为了测量矗立在高速公路上水平地面上的交通警示牌的高度CD,在与M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,则警示牌CD的高度为
米(结果保留根号).
18.再如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为多少
km.
三.解答题(共6小题)
19.计算:
2sin60°?tan30°+cos230°﹣tan45°.
20.(1)计算:tan60°+9tan30°﹣8sin60°+2cos45°;
(2)在△ABC中,∠C=90°,AC=,BC=,求∠A的度数.
21.在Rt△ABC中,已知∠C=90°,a=19,c=19,解这个直角三角形.
22.5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰完成峰顶测量任务,受此消息鼓舞,某数学小组开展了一次测量小山高度的活动,如图,该数学小组从地面A处出发,沿坡角为53°的山坡AB直线上行一段距离到达B处,再沿着坡角为22°的山坡BC直线上行600米到达C处,通过测量数据计算出小山高CD=500m.求该数学小组行进的水平距离AD(结果精确到1m).(参考数据:sin22°≈0.37,cos22°≈0.92,tan22°≈0.32,sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
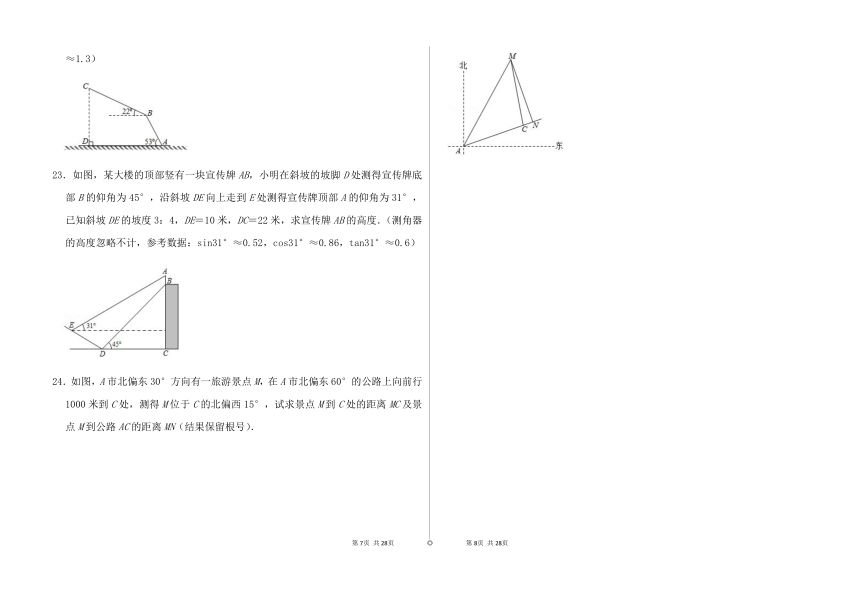
23.如图,某大楼的顶部竖有一块宣传牌AB,小明在斜坡的坡脚D处测得宣传牌底部B的仰角为45°,沿斜坡DE向上走到E处测得宣传牌顶部A的仰角为31°,已知斜坡DE的坡度3:4,DE=10米,DC=22米,求宣传牌AB的高度.(测角器的高度忽略不计,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)
24.如图,A市北偏东30°方向有一旅游景点M,在A市北偏东60°的公路上向前行1000米到C处,测得M位于C的北偏西15°,试求景点M到C处的距离MC及景点M到公路AC的距离MN(结果保留根号).
参考答案与试题解析
一.选择题(共12小题)
1.【分析】根据勾股定理求出BC,根据锐角三角函数的定义计算,判断即可.
【解答】解:A、由勾股定理得,BC===,本选项说法错误;
B、∵sinA==,tanB===,
∴sinA<tanB,本选项说法错误;
C、cosA==,本选项说法正确;
D、∵tanA==,cosB==,
∴tanA>cosB,本选项说法错误;
故选:C.
【点评】本题考查的是锐角三角函数的定义、勾股定理的应用,锐角A的对边a与斜边c的比叫做∠A的正弦;锐角A的邻边b与斜边c的比叫做∠A的余弦;锐角A的对边a与邻边b的比叫做∠A的正切.
2.【分析】根据特殊锐角的三角函数值,得出75°﹣θ=30°,进而求出答案.
【解答】解:∵sin30°=,
∴75°﹣θ=30°,
∴θ=45°,
故选:C.
【点评】本题考查特殊锐角的三角函数值,掌握特殊锐角的三角函数值是正确计算的前提.
3.【分析】直接利用特殊角的三角函数值代入得出答案.
【解答】解:sin230°+cos260°=()2+()2
=+
=.
故选:A.
【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
4.【分析】先由直角三角形的性质得∠ABD=∠C,再由锐角三角函数定义即可得出答案.
【解答】解:∵∠ABC=90°,
∴∠A+∠C=90°,
∵BD⊥AC,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∴∠ABD=∠C,
∵AB=2BC,
∴tan∠ABD=tan∠C==2,
故选:A.
【点评】此题考查了解直角三角形,锐角三角函数的定义等知识,解题的关键是证出∠ABD=∠C.
5.【分析】根据网格,设出小正方形的边长为1,表示出AD=DC=,再根据平行线分线段成比例定理可得出DP=DC,进而在Rt△ADP中,由正切的意义求值即可.
【解答】解:设小正方形的边长为1,
由图形可知,,
∴△ADC是等腰直角三角形,
∴AD⊥DC.
∵AC∥BD,
∴,
∴PC=2DP,
∴AD=DC=3DP,
∴.
故选:B.
【点评】本题考查解直角三角形,掌握直角三角形的边角关系和平行线分线段成比例定理是解决问题的前提.
6.【分析】根据作图的方法得出△OBC是等边三角形,进而利用特殊角的三角函数值求出答案.
【解答】解:连接BC,
由题意可得:OB=OC=BC,
则△OBC是等边三角形,
故tan∠AOC=tan60°=.
故选:D.
【点评】此题主要考查了特殊角的三角函数值以及基本作图方法,正确得出△OBC是等边三角形是解题关键.
7.【分析】直接利用坡度的定义,进而得出坡角的度数.
【解答】解:∵水库的拦水坝斜坡的坡度为1:,
∴设这个拦水坝的坡角为α,则tanα==,
∴这个拦水坝的坡角为:30°.
故选:A.
【点评】本题考查了解直角三角形的应用﹣﹣坡度坡角问题,正确掌握坡角的定义是解题的关键.
8.【分析】证出BD=BC=5,根据锐角三角函数关系得出方程,解方程即可.
【解答】解:由题意可得:∠CDB=∠DCB=45°,
∴BD=BC=5,
设AC=xm,则AB=(x+5)m,
在Rt△ABD中,tan60°=,
则=,
解得:x=5﹣5,
即AC的长度是(5﹣5)m;
故选:D.
【点评】此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键.
9.【分析】延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.
【解答】解:如图,延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,BF:CF=1:,
∴设BF=k,则CF=k,
∴BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=6,
∵DF=DC+CF,
∴DF=40+6
在Rt△AEH中,tan∠AEH=,
∴AH=tan37°×(40+6)≈37.785(米),
∵BH=BF﹣FH,
∴BH=6﹣1.5=4.5.
∵AB=AH﹣HB,
∴AB=37.785﹣4.5≈33.3.
答:大楼AB的高度约为33.3米.
故选:C.
【点评】本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.
10.【分析】先根据题意求出∠AOB,再根据直角三角形的性质解答即可.
【解答】解:由题意得,∠AOB=90°﹣60°=30°,OA=300m,
∴AB=OA=150(m),
故选:C.
【点评】本题考查的是解直角三角形的应用﹣方向角问题,掌握方向角的概念、熟记含30度角的直角三角形的性质是解题的关键.
11.【分析】过点C作CD⊥AB于D,CD是直角三角形ACD和CBD的公共直角边,要先求出CD的值然后再求AD,BD的值,进而得出AB的长.
【解答】解:过点C作CD⊥AB于D,如图所示:
由题意得:∠ACD=45°,∠DCB=α,
在Rt△BCD中,BC=m,
∴DB=BCsinα°=m?sinα(米),CD=BCcosα=m?cosα(米),
在Rt△ACD中,AD=CD=m?cosα(米),
∴AB=AD+DB=m(cosα+sinα)(米).
故选:A.
【点评】本题考查了解直角三角形的应用﹣方向角问题;熟练掌握解直角三角形是解题的关键.
12.【分析】根据等腰三角形的三线合一性质得∠ACB的度数,进而得∠BDE的度数,再解直角三角形得结果.
【解答】解:∵∠BAC=40°,AB=AC,
∴∠ACB=∠ABC=70°,
∵DE⊥BC,
∴∠DEB=90°,
∴∠BDE=90°﹣70°=20°,
∴DE=BD?cos20°=140cos20°,
故选:B.
【点评】本题主要考查了解直角三角形,等腰三角形的性质,关键是构造直角三角形求得∠BDE的度数.
二.填空题(共6小题)
13.【分析】先根据勾股定理求出AB的长,再利用正弦函数的概念求解即可.
【解答】解:在Rt△ABC中,∵∠C=90°,AC=4,BC=6,
∴AB===2,
则sinA===,
故答案为:.
【点评】本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理和正弦函数的定义.
14.【分析】直接利用非负数的性质、特殊角的三角函数值进而得出∴∠A=30°,∠B=30°,即可得出答案.
【解答】解:∵|sinA﹣|+(cosB﹣)2=0,
∴sinA﹣=0,cosB﹣=0,
∴sinA=,cosB=,
∴∠A=30°,∠B=30°,
∴△ABC的形状是等腰三角形.
故答案为:等腰三角形.
【点评】此题主要考查了非负数的性质以及特殊角的三角函数值,正确记忆相关数据是解题关键.
15.【分析】分两种情况:①当△ABC是锐角三角形时;②当△ABC是钝角三角形时;先由锐角三角函数定义和勾股定理求出CD=1,AD=3,再由勾股定理求出BD=4,然后由勾股定理和锐角三角函数定义即可得出答案.
【解答】解:分两种情况:
①当△ABC是锐角三角形时,如图1所示:
∵AD是△ABC的高,
∴AD⊥BC,
∴∠ADB=∠ADC=90°,
∴tan∠CAD==,
设CD=x(x>0),则AD=3x,
在Rt△ACD中,由勾股定理得:x2+(3x)2=()2,
解得:x=1,
∴CD=1,AD=3,
∴BD===4,
∴BC=BD+CD=5,
∴BC=AB,
∴∠BAC=∠C,
∴tan∠BAC=tan∠C==3;
②当△ABC是钝角三角形时,如图2所示:
同①得:CD=1,AD=3,BD=4,
∴BC=BD﹣CD=3,
过C作CE⊥AB于E,
∵△ABC的面积=AB×CE=BC×AD,
∴CE===,
∴BE===,
∴AE=AB﹣BE=5﹣=,
∴tan∠BAC===;
综上所述,tan∠BAC的值为3或,
故答案为:3或.
【点评】本题考查了解直角三角形、等腰三角形的判定与性质、勾股定理、锐角三角函数定义等知识;熟练掌握勾股定理和锐角三角函数定义是解题的关键.
16.【分析】直接利用坡度的定义得出AD的长,再利用勾股定理得出BD的长,进而得出答案.
【解答】解:∵斜面AC的坡度(CD与AD的比)为1:2,CD=3米,
∴AD=6米,
∵AB=10米,AD=6米,
∴BD==8(米),
∴BC=8﹣3=5(米),
∴旗杆BC的高度为5米.
故答案为:5.
【点评】此题主要考查了解直角三角形的应用以及勾股定理,正确得出AD的长是解题关键.
17.【分析】根据CD=CM﹣DM,想办法求出CM、DM即可解决问题.
【解答】解:在Rt△ADM中,
∵AM=4,∠MAD=45°,
∴DM=AM=4,
∵AB=8,
∴MB=AM+AB=12,
在Rt△BCM中,∵∠MBC=30°,
∴MC=MBtan30°=4,
∴DC=MC﹣DM=(4﹣4)(米)
答:警示牌的高度CD为(4﹣4)米,
故答案为:(4﹣4).
【点评】本题考查解直角三角形﹣仰角俯角问题,锐角三角函数等知识,解题的关键是灵活所学知识解决问题,属于中考常考题型.
18.【分析】过B作BE⊥AC于E,过C作CF∥AD,证出∠ACB=60°,由题意得∠CAB=65°﹣20°=45°,AB=30km,解直角三角形求出AE、CE的长,即可得到答案.
【解答】解:如图,过B作BE⊥AC于E,过C作CF∥AD,
则CF∥AD∥BG,∠AEB=∠CEB=90°,
∴∠ACF=∠CAD=20°,∠BCF=∠CBG=40°,
∴∠ACB=20°+40°=60°,
由题意得,∠CAB=65°﹣20°=45°,AB=30km,
在Rt△ABE中,∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∵AB=30km,
∴AE=BE=AB=30(km),
在Rt△CBE中,∵∠ACB=60°,tan∠ACB=,
∴CE===10(km),
∴AC=AE+CE=30+10(km),
∴A,C两港之间的距离为(30+10)km,
故答案为:(30+10).
【点评】本题考查了解直角三角形的应用,方向角问题,等腰直角三角形的判定与性质等知识;熟练掌握解直角三角形,作出辅助线构造直角三角形是解题的关键.
三.解答题(共6小题)
19.【分析】将特殊锐角的三角函数值代入计算即可.
【解答】解:2sin60°?tan30°+cos230°﹣tan45°
=2××+()2﹣1
=1+﹣1
=.
【点评】本题考查特殊锐角的三角函数值,掌握特殊锐角的三角函数值是正确计算的前提.
20.【分析】(1)代入特殊锐角的三角函数值进行计算即可;
(2)由锐角三角函数定义的定义得tanA==,即可得出答案.
【解答】解:(1)tan60°+9tan30°﹣8sin60°+2cos45°
=+9×﹣8×+2×
=+3﹣4+
=;
(2)∵∠C=90°,AC=,BC=,
∴tanA===,
∴∠A=60°.
【点评】本题考查了解直角三角形以及特殊锐角的三角函数值等知识;熟练掌握特殊锐角的三角函数值和锐角三角函数定义是解题的关键.
21.【分析】利用直角三角形的边角关系,选择合适的关系式进行解答即可.
【解答】解:在Rt△ABC中,∠C=90°,a=19,c=19,
∴b==19,
∵tanA==1,
∴∠A=45°,
∴∠B=90°﹣∠A=45°,
因此,b=19,∠A=∠B=45°.
【点评】本题考查解直角三角形,掌握直角三角形的边角关系是正确求解的关键.
22.【分析】过B作BE⊥CD于E,过B作BH⊥AD于H,则四边形BEDH是矩形,于是得到DE=BH,BE=DH,解直角三角形即可得到结论.
【解答】解:过B作BE⊥CD于E,过B作BH⊥AD于H,
则四边形BEDH是矩形,
∴DE=BH,BE=DH,
在Rt△ACE中,∵BC=600,∠CBE=22°,
∴CE=BC?sin22°=600×0.37=222(m),BE=BC?cos22°=600×0.92=552(m),
∴DH=BE=552m,
∵CD=500m,
∴BH=DE=CD﹣CE=500﹣222=278(m),
在Rt△ABH中,∵∠BAH=53°,
∴tan53°=,
∴AH=≈214(m),
∴AD=AH+DH=214+552=766(m),
答:该数学小组行进的水平距离AD为766m.
【点评】此题主要考查了解直角三角形的应用,熟练利用锐角三角函数关系得出是解题关键.
23.【分析】过E分别作CD、AC的垂线,设垂足为F、G,于是得到CF=EG,CG=EF,解直角三角形即可得到结论.
【解答】解:过E分别作CD、AC的垂线,设垂足为F、G,
则CF=EG,CG=EF,
在Rt△EFD中,∵斜坡DE的坡度3:4,DE=10米,
∴设EF=3x米,DF=4x米,
∴DE==5x=10,
∴x=2,
∴EF=6米,DF=8米,
在Rt△BCD中,∠BDC=45°,
∴BC=CD=22米,
∴BG=BC﹣CG=22﹣6=16(米),
在Rt△AEG中,AG=EG?tan31°=30×0.6=18(米),
∴AB=AG﹣BG=18﹣16=2(米),
答:宣传牌AB的高度为2米.
【点评】此题考查了解直角三角形的应用﹣仰角、俯角问题,解直角三角形的应用﹣坡角坡度问题,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.
24.【分析】由题意可知∠MAC=30°,∠MCN=75°,则∠AMC=∠MCN﹣∠MAC=45°,过C作CH⊥AM交AM于点H,由直角三角形的性质得HCAC=500(m),AH=HC=500(m),再求出,然后由三角形面积关系求出MN即可.
【解答】解:由题意可知:∠MAC=60°﹣30°=30°,∠MCN=15°+60°=75°,
∴∠AMC=∠MCN﹣∠MAC=75°﹣30°=45°,
过C作CH⊥AM交AM于点H,如图所示:
在Rt△ACH中,∠MAC=30°,AC=1000m,
∴HCAC=500(m),AH=HC=500(m),
在Rt△HMC中,,
∴?MN,
即:,
∴,
即MC的长度为米,MN的长度为米.
【点评】本题考查了解直角三角形的应用﹣方向角问题以及含30°角的直角三角形的性质等知识;熟练掌握方向角的概念,正确作出辅助线构造直角三角形是解题的关键.
第1页
共2页
◎
第2页
共2页
测试题
一.选择题(共12小题)
1.在△ABC中,∠C=90°,若AC=3,AB=4,则( )
A.BC=5
B.sinA>tanB
C.cosA=
D.tanA=cosB
2.若sin(75°﹣θ)的值是,则θ=( )
A.15°
B.30°
C.45°
D.60°
3.计算sin230°+cos260°的结果为( )
A.
B.
C.1
D.
4.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D,AB=2BC,则tan∠ABD的值为( )
A.2
B.
C.
D.
5.如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD=( )
A.
B.3
C.
D.2
6.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则tan∠AOC的值为( )
A.
B.
C.
D.
7.已知水库的拦水坝斜坡的坡度为1:,则这个拦水坝的坡角为( )度.
A.30
B.45
C.60
D.90
8.如图,这是某市政道路的交通指示牌,BD的距离为5m,从D点测得指示牌顶端A点和底端C点的仰角分别是60°和45°,则指示牌的高度,即AC的长度是( )m.
A.5
B.5
C.5﹣5
D.5﹣5
9.某兴趣小组想测量一座大楼AB的高度,如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:.在离C点40米的D处,用测量仪测得大楼顶端A的仰角为37°,测角仪DE的高度为1.5米,求大楼AB的高度约为多少米?( )(结果精确到0.1米)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73.)
A.39.3
B.37.8
C.33.3
D.25.7
10.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距300m,则图书馆A到公路的距离AB为( )
A.150m
B.150m
C.150m
D.100m
11.如图,小明在C处看到西北方向上有一凉亭A,北偏东α°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=m米,则A、B两点相距( )
A.m(cosα+sinα)米
B.m(cosα﹣sinα)米
C.米
D.米
12.人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,则点D离地面的高度DE为( )
A.140sin20°
cm
B.140cos20°
cm
C.140sin40°
cm
D.140cos40°
cm
二.填空题(共6小题)
13.如图,Rt△ABC中,∠C=90°,AC=4,BC=6,则sinA=
.
14.在△ABC中,若|sinA﹣|+(cosB﹣)2=0,则△ABC的形状是
.
15.已知:AD是△ABC的高,其中tan∠CAD=,AB=5,AC=,则tan∠BAC的值为
.
16.如图,斜面AC的坡度(CD与AD的比)为1:2,坡顶有一旗杆BC,顶端B点与A点有一条彩带相连,已知CD=3米,AB=10米,则旗杆BC的高度为
米.
17.如图,为了测量矗立在高速公路上水平地面上的交通警示牌的高度CD,在与M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,则警示牌CD的高度为
米(结果保留根号).
18.再如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为多少
km.
三.解答题(共6小题)
19.计算:
2sin60°?tan30°+cos230°﹣tan45°.
20.(1)计算:tan60°+9tan30°﹣8sin60°+2cos45°;
(2)在△ABC中,∠C=90°,AC=,BC=,求∠A的度数.
21.在Rt△ABC中,已知∠C=90°,a=19,c=19,解这个直角三角形.
22.5月27日,2020珠峰高程测量登山队成功登顶珠穆朗玛峰完成峰顶测量任务,受此消息鼓舞,某数学小组开展了一次测量小山高度的活动,如图,该数学小组从地面A处出发,沿坡角为53°的山坡AB直线上行一段距离到达B处,再沿着坡角为22°的山坡BC直线上行600米到达C处,通过测量数据计算出小山高CD=500m.求该数学小组行进的水平距离AD(结果精确到1m).(参考数据:sin22°≈0.37,cos22°≈0.92,tan22°≈0.32,sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
23.如图,某大楼的顶部竖有一块宣传牌AB,小明在斜坡的坡脚D处测得宣传牌底部B的仰角为45°,沿斜坡DE向上走到E处测得宣传牌顶部A的仰角为31°,已知斜坡DE的坡度3:4,DE=10米,DC=22米,求宣传牌AB的高度.(测角器的高度忽略不计,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)
24.如图,A市北偏东30°方向有一旅游景点M,在A市北偏东60°的公路上向前行1000米到C处,测得M位于C的北偏西15°,试求景点M到C处的距离MC及景点M到公路AC的距离MN(结果保留根号).
参考答案与试题解析
一.选择题(共12小题)
1.【分析】根据勾股定理求出BC,根据锐角三角函数的定义计算,判断即可.
【解答】解:A、由勾股定理得,BC===,本选项说法错误;
B、∵sinA==,tanB===,
∴sinA<tanB,本选项说法错误;
C、cosA==,本选项说法正确;
D、∵tanA==,cosB==,
∴tanA>cosB,本选项说法错误;
故选:C.
【点评】本题考查的是锐角三角函数的定义、勾股定理的应用,锐角A的对边a与斜边c的比叫做∠A的正弦;锐角A的邻边b与斜边c的比叫做∠A的余弦;锐角A的对边a与邻边b的比叫做∠A的正切.
2.【分析】根据特殊锐角的三角函数值,得出75°﹣θ=30°,进而求出答案.
【解答】解:∵sin30°=,
∴75°﹣θ=30°,
∴θ=45°,
故选:C.
【点评】本题考查特殊锐角的三角函数值,掌握特殊锐角的三角函数值是正确计算的前提.
3.【分析】直接利用特殊角的三角函数值代入得出答案.
【解答】解:sin230°+cos260°=()2+()2
=+
=.
故选:A.
【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
4.【分析】先由直角三角形的性质得∠ABD=∠C,再由锐角三角函数定义即可得出答案.
【解答】解:∵∠ABC=90°,
∴∠A+∠C=90°,
∵BD⊥AC,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∴∠ABD=∠C,
∵AB=2BC,
∴tan∠ABD=tan∠C==2,
故选:A.
【点评】此题考查了解直角三角形,锐角三角函数的定义等知识,解题的关键是证出∠ABD=∠C.
5.【分析】根据网格,设出小正方形的边长为1,表示出AD=DC=,再根据平行线分线段成比例定理可得出DP=DC,进而在Rt△ADP中,由正切的意义求值即可.
【解答】解:设小正方形的边长为1,
由图形可知,,
∴△ADC是等腰直角三角形,
∴AD⊥DC.
∵AC∥BD,
∴,
∴PC=2DP,
∴AD=DC=3DP,
∴.
故选:B.
【点评】本题考查解直角三角形,掌握直角三角形的边角关系和平行线分线段成比例定理是解决问题的前提.
6.【分析】根据作图的方法得出△OBC是等边三角形,进而利用特殊角的三角函数值求出答案.
【解答】解:连接BC,
由题意可得:OB=OC=BC,
则△OBC是等边三角形,
故tan∠AOC=tan60°=.
故选:D.
【点评】此题主要考查了特殊角的三角函数值以及基本作图方法,正确得出△OBC是等边三角形是解题关键.
7.【分析】直接利用坡度的定义,进而得出坡角的度数.
【解答】解:∵水库的拦水坝斜坡的坡度为1:,
∴设这个拦水坝的坡角为α,则tanα==,
∴这个拦水坝的坡角为:30°.
故选:A.
【点评】本题考查了解直角三角形的应用﹣﹣坡度坡角问题,正确掌握坡角的定义是解题的关键.
8.【分析】证出BD=BC=5,根据锐角三角函数关系得出方程,解方程即可.
【解答】解:由题意可得:∠CDB=∠DCB=45°,
∴BD=BC=5,
设AC=xm,则AB=(x+5)m,
在Rt△ABD中,tan60°=,
则=,
解得:x=5﹣5,
即AC的长度是(5﹣5)m;
故选:D.
【点评】此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键.
9.【分析】延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.
【解答】解:如图,延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,BF:CF=1:,
∴设BF=k,则CF=k,
∴BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=6,
∵DF=DC+CF,
∴DF=40+6
在Rt△AEH中,tan∠AEH=,
∴AH=tan37°×(40+6)≈37.785(米),
∵BH=BF﹣FH,
∴BH=6﹣1.5=4.5.
∵AB=AH﹣HB,
∴AB=37.785﹣4.5≈33.3.
答:大楼AB的高度约为33.3米.
故选:C.
【点评】本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.
10.【分析】先根据题意求出∠AOB,再根据直角三角形的性质解答即可.
【解答】解:由题意得,∠AOB=90°﹣60°=30°,OA=300m,
∴AB=OA=150(m),
故选:C.
【点评】本题考查的是解直角三角形的应用﹣方向角问题,掌握方向角的概念、熟记含30度角的直角三角形的性质是解题的关键.
11.【分析】过点C作CD⊥AB于D,CD是直角三角形ACD和CBD的公共直角边,要先求出CD的值然后再求AD,BD的值,进而得出AB的长.
【解答】解:过点C作CD⊥AB于D,如图所示:
由题意得:∠ACD=45°,∠DCB=α,
在Rt△BCD中,BC=m,
∴DB=BCsinα°=m?sinα(米),CD=BCcosα=m?cosα(米),
在Rt△ACD中,AD=CD=m?cosα(米),
∴AB=AD+DB=m(cosα+sinα)(米).
故选:A.
【点评】本题考查了解直角三角形的应用﹣方向角问题;熟练掌握解直角三角形是解题的关键.
12.【分析】根据等腰三角形的三线合一性质得∠ACB的度数,进而得∠BDE的度数,再解直角三角形得结果.
【解答】解:∵∠BAC=40°,AB=AC,
∴∠ACB=∠ABC=70°,
∵DE⊥BC,
∴∠DEB=90°,
∴∠BDE=90°﹣70°=20°,
∴DE=BD?cos20°=140cos20°,
故选:B.
【点评】本题主要考查了解直角三角形,等腰三角形的性质,关键是构造直角三角形求得∠BDE的度数.
二.填空题(共6小题)
13.【分析】先根据勾股定理求出AB的长,再利用正弦函数的概念求解即可.
【解答】解:在Rt△ABC中,∵∠C=90°,AC=4,BC=6,
∴AB===2,
则sinA===,
故答案为:.
【点评】本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理和正弦函数的定义.
14.【分析】直接利用非负数的性质、特殊角的三角函数值进而得出∴∠A=30°,∠B=30°,即可得出答案.
【解答】解:∵|sinA﹣|+(cosB﹣)2=0,
∴sinA﹣=0,cosB﹣=0,
∴sinA=,cosB=,
∴∠A=30°,∠B=30°,
∴△ABC的形状是等腰三角形.
故答案为:等腰三角形.
【点评】此题主要考查了非负数的性质以及特殊角的三角函数值,正确记忆相关数据是解题关键.
15.【分析】分两种情况:①当△ABC是锐角三角形时;②当△ABC是钝角三角形时;先由锐角三角函数定义和勾股定理求出CD=1,AD=3,再由勾股定理求出BD=4,然后由勾股定理和锐角三角函数定义即可得出答案.
【解答】解:分两种情况:
①当△ABC是锐角三角形时,如图1所示:
∵AD是△ABC的高,
∴AD⊥BC,
∴∠ADB=∠ADC=90°,
∴tan∠CAD==,
设CD=x(x>0),则AD=3x,
在Rt△ACD中,由勾股定理得:x2+(3x)2=()2,
解得:x=1,
∴CD=1,AD=3,
∴BD===4,
∴BC=BD+CD=5,
∴BC=AB,
∴∠BAC=∠C,
∴tan∠BAC=tan∠C==3;
②当△ABC是钝角三角形时,如图2所示:
同①得:CD=1,AD=3,BD=4,
∴BC=BD﹣CD=3,
过C作CE⊥AB于E,
∵△ABC的面积=AB×CE=BC×AD,
∴CE===,
∴BE===,
∴AE=AB﹣BE=5﹣=,
∴tan∠BAC===;
综上所述,tan∠BAC的值为3或,
故答案为:3或.
【点评】本题考查了解直角三角形、等腰三角形的判定与性质、勾股定理、锐角三角函数定义等知识;熟练掌握勾股定理和锐角三角函数定义是解题的关键.
16.【分析】直接利用坡度的定义得出AD的长,再利用勾股定理得出BD的长,进而得出答案.
【解答】解:∵斜面AC的坡度(CD与AD的比)为1:2,CD=3米,
∴AD=6米,
∵AB=10米,AD=6米,
∴BD==8(米),
∴BC=8﹣3=5(米),
∴旗杆BC的高度为5米.
故答案为:5.
【点评】此题主要考查了解直角三角形的应用以及勾股定理,正确得出AD的长是解题关键.
17.【分析】根据CD=CM﹣DM,想办法求出CM、DM即可解决问题.
【解答】解:在Rt△ADM中,
∵AM=4,∠MAD=45°,
∴DM=AM=4,
∵AB=8,
∴MB=AM+AB=12,
在Rt△BCM中,∵∠MBC=30°,
∴MC=MBtan30°=4,
∴DC=MC﹣DM=(4﹣4)(米)
答:警示牌的高度CD为(4﹣4)米,
故答案为:(4﹣4).
【点评】本题考查解直角三角形﹣仰角俯角问题,锐角三角函数等知识,解题的关键是灵活所学知识解决问题,属于中考常考题型.
18.【分析】过B作BE⊥AC于E,过C作CF∥AD,证出∠ACB=60°,由题意得∠CAB=65°﹣20°=45°,AB=30km,解直角三角形求出AE、CE的长,即可得到答案.
【解答】解:如图,过B作BE⊥AC于E,过C作CF∥AD,
则CF∥AD∥BG,∠AEB=∠CEB=90°,
∴∠ACF=∠CAD=20°,∠BCF=∠CBG=40°,
∴∠ACB=20°+40°=60°,
由题意得,∠CAB=65°﹣20°=45°,AB=30km,
在Rt△ABE中,∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∵AB=30km,
∴AE=BE=AB=30(km),
在Rt△CBE中,∵∠ACB=60°,tan∠ACB=,
∴CE===10(km),
∴AC=AE+CE=30+10(km),
∴A,C两港之间的距离为(30+10)km,
故答案为:(30+10).
【点评】本题考查了解直角三角形的应用,方向角问题,等腰直角三角形的判定与性质等知识;熟练掌握解直角三角形,作出辅助线构造直角三角形是解题的关键.
三.解答题(共6小题)
19.【分析】将特殊锐角的三角函数值代入计算即可.
【解答】解:2sin60°?tan30°+cos230°﹣tan45°
=2××+()2﹣1
=1+﹣1
=.
【点评】本题考查特殊锐角的三角函数值,掌握特殊锐角的三角函数值是正确计算的前提.
20.【分析】(1)代入特殊锐角的三角函数值进行计算即可;
(2)由锐角三角函数定义的定义得tanA==,即可得出答案.
【解答】解:(1)tan60°+9tan30°﹣8sin60°+2cos45°
=+9×﹣8×+2×
=+3﹣4+
=;
(2)∵∠C=90°,AC=,BC=,
∴tanA===,
∴∠A=60°.
【点评】本题考查了解直角三角形以及特殊锐角的三角函数值等知识;熟练掌握特殊锐角的三角函数值和锐角三角函数定义是解题的关键.
21.【分析】利用直角三角形的边角关系,选择合适的关系式进行解答即可.
【解答】解:在Rt△ABC中,∠C=90°,a=19,c=19,
∴b==19,
∵tanA==1,
∴∠A=45°,
∴∠B=90°﹣∠A=45°,
因此,b=19,∠A=∠B=45°.
【点评】本题考查解直角三角形,掌握直角三角形的边角关系是正确求解的关键.
22.【分析】过B作BE⊥CD于E,过B作BH⊥AD于H,则四边形BEDH是矩形,于是得到DE=BH,BE=DH,解直角三角形即可得到结论.
【解答】解:过B作BE⊥CD于E,过B作BH⊥AD于H,
则四边形BEDH是矩形,
∴DE=BH,BE=DH,
在Rt△ACE中,∵BC=600,∠CBE=22°,
∴CE=BC?sin22°=600×0.37=222(m),BE=BC?cos22°=600×0.92=552(m),
∴DH=BE=552m,
∵CD=500m,
∴BH=DE=CD﹣CE=500﹣222=278(m),
在Rt△ABH中,∵∠BAH=53°,
∴tan53°=,
∴AH=≈214(m),
∴AD=AH+DH=214+552=766(m),
答:该数学小组行进的水平距离AD为766m.
【点评】此题主要考查了解直角三角形的应用,熟练利用锐角三角函数关系得出是解题关键.
23.【分析】过E分别作CD、AC的垂线,设垂足为F、G,于是得到CF=EG,CG=EF,解直角三角形即可得到结论.
【解答】解:过E分别作CD、AC的垂线,设垂足为F、G,
则CF=EG,CG=EF,
在Rt△EFD中,∵斜坡DE的坡度3:4,DE=10米,
∴设EF=3x米,DF=4x米,
∴DE==5x=10,
∴x=2,
∴EF=6米,DF=8米,
在Rt△BCD中,∠BDC=45°,
∴BC=CD=22米,
∴BG=BC﹣CG=22﹣6=16(米),
在Rt△AEG中,AG=EG?tan31°=30×0.6=18(米),
∴AB=AG﹣BG=18﹣16=2(米),
答:宣传牌AB的高度为2米.
【点评】此题考查了解直角三角形的应用﹣仰角、俯角问题,解直角三角形的应用﹣坡角坡度问题,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.
24.【分析】由题意可知∠MAC=30°,∠MCN=75°,则∠AMC=∠MCN﹣∠MAC=45°,过C作CH⊥AM交AM于点H,由直角三角形的性质得HCAC=500(m),AH=HC=500(m),再求出,然后由三角形面积关系求出MN即可.
【解答】解:由题意可知:∠MAC=60°﹣30°=30°,∠MCN=15°+60°=75°,
∴∠AMC=∠MCN﹣∠MAC=75°﹣30°=45°,
过C作CH⊥AM交AM于点H,如图所示:
在Rt△ACH中,∠MAC=30°,AC=1000m,
∴HCAC=500(m),AH=HC=500(m),
在Rt△HMC中,,
∴?MN,
即:,
∴,
即MC的长度为米,MN的长度为米.
【点评】本题考查了解直角三角形的应用﹣方向角问题以及含30°角的直角三角形的性质等知识;熟练掌握方向角的概念,正确作出辅助线构造直角三角形是解题的关键.
第1页
共2页
◎
第2页
共2页
