11.2.1三角形内角和 教学设计
图片预览

文档简介
八年级数学上册教学设计
课题
11.2.1三角形内角和
教学
目标
了解三角形内角,
掌握三角形内角和定理的证明
3.会用三角形内角和进行角度的计算
教学
重点
掌握三角形内角和的性质
教学
难点
三角形内角和定理的证明方法
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、三角形内角和定理的证明
1.在所准备的三角形硬纸片上标出三个内角的编码
2.让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出∠BCD
的度数,可得到
方法一:
3.
剪下∠A,按图拼在一起,从而还可得到
4.把∠B和∠C
剪下按图拼在一起,用量角器量一量∠MAN
的度数,会得到什么结果。
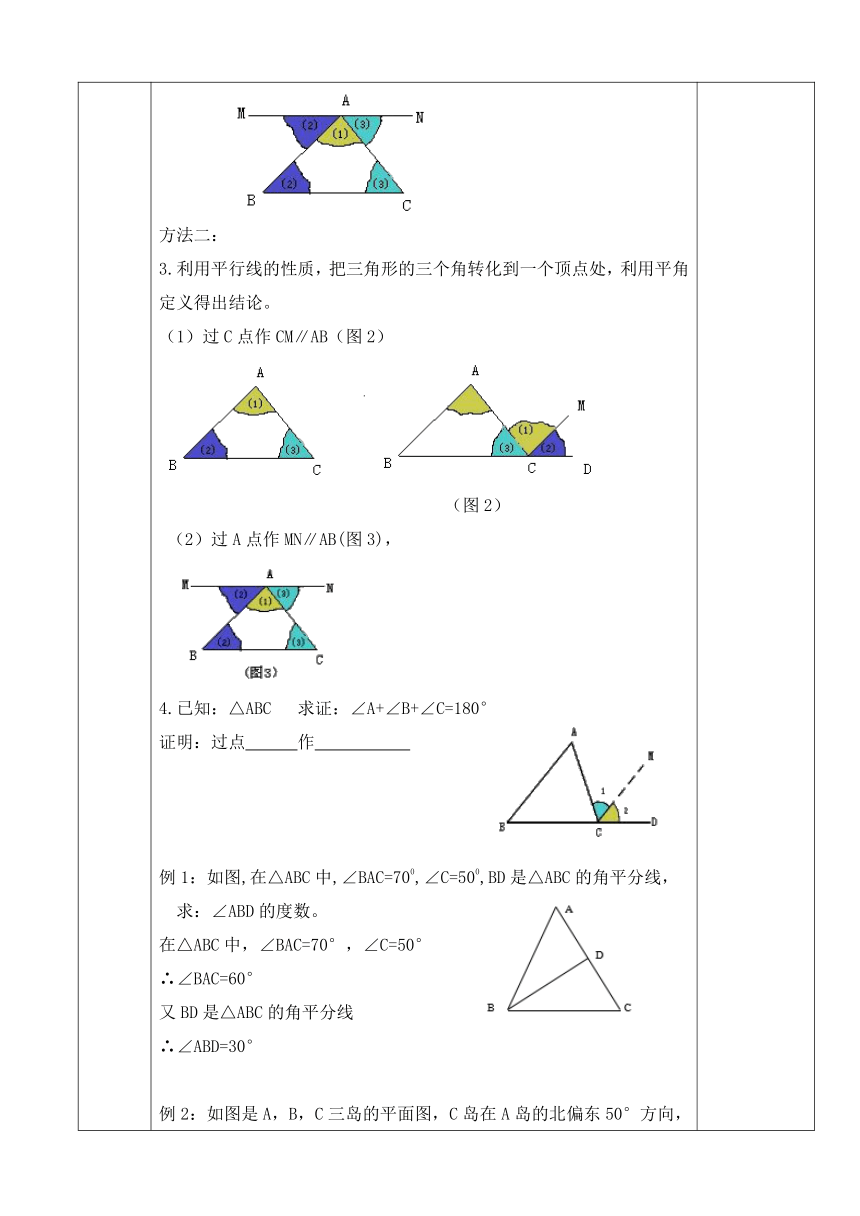
方法二:
3.利用平行线的性质,把三角形的三个角转化到一个顶点处,利用平角定义得出结论。
(1)过C点作CM∥AB(图2)
(图2)
(2)过A点作MN∥AB(图3),
4.已知:△ABC
求证:∠A+∠B+∠C=180°
证明:过点
作
例1:如图,在△ABC中,∠BAC=700,∠C=500,BD是△ABC的角平分线,
求:∠ABD的度数。
在△ABC中,∠BAC=70°,∠C=50°
∴∠BAC=60°
又BD是△ABC的角平分线
∴∠ABD=30°
例2:如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB呢?
设计问题:(1)
请你解释一下这些方位角。
(2)
∠ACB是哪个三角形的内角?
(3)
有不同解法请你的同伴交流。
课堂作业:
1、在△ABC中,若∠A=60°,∠C=40°,则∠B=
,
2、在△ABC中,若∠C=80°,则∠B+∠A=
3、在△ABC中,若∠B+∠C=160°,则∠A=
4、已知△ABC中,∠B=65°,∠C=45°,AD是∠ABC的高线,AE是∠BAC的平分线,则∠DAE=__________________.
6、如图所示,已知直线AB∥CD,∠=125°,∠A=45°
,
求∠E的度数?
7、△ABC中,∠A+∠B=100°,∠C=2∠A,求∠A,∠B的度数
8、如图,在△ABC中,∠BAC=800,∠C=600,BD是△ABC的角平分线,
求:∠ABD的度数。
板
书
设
计
1.三角形内角和是180°。
2.几何语言叙述:
在△ABC中,∠A+∠B+∠C=180°。
教
学
反
思
课题
11.2.1三角形内角和
教学
目标
了解三角形内角,
掌握三角形内角和定理的证明
3.会用三角形内角和进行角度的计算
教学
重点
掌握三角形内角和的性质
教学
难点
三角形内角和定理的证明方法
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、三角形内角和定理的证明
1.在所准备的三角形硬纸片上标出三个内角的编码
2.让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出∠BCD
的度数,可得到
方法一:
3.
剪下∠A,按图拼在一起,从而还可得到
4.把∠B和∠C
剪下按图拼在一起,用量角器量一量∠MAN
的度数,会得到什么结果。
方法二:
3.利用平行线的性质,把三角形的三个角转化到一个顶点处,利用平角定义得出结论。
(1)过C点作CM∥AB(图2)
(图2)
(2)过A点作MN∥AB(图3),
4.已知:△ABC
求证:∠A+∠B+∠C=180°
证明:过点
作
例1:如图,在△ABC中,∠BAC=700,∠C=500,BD是△ABC的角平分线,
求:∠ABD的度数。
在△ABC中,∠BAC=70°,∠C=50°
∴∠BAC=60°
又BD是△ABC的角平分线
∴∠ABD=30°
例2:如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB呢?
设计问题:(1)
请你解释一下这些方位角。
(2)
∠ACB是哪个三角形的内角?
(3)
有不同解法请你的同伴交流。
课堂作业:
1、在△ABC中,若∠A=60°,∠C=40°,则∠B=
,
2、在△ABC中,若∠C=80°,则∠B+∠A=
3、在△ABC中,若∠B+∠C=160°,则∠A=
4、已知△ABC中,∠B=65°,∠C=45°,AD是∠ABC的高线,AE是∠BAC的平分线,则∠DAE=__________________.
6、如图所示,已知直线AB∥CD,∠=125°,∠A=45°
,
求∠E的度数?
7、△ABC中,∠A+∠B=100°,∠C=2∠A,求∠A,∠B的度数
8、如图,在△ABC中,∠BAC=800,∠C=600,BD是△ABC的角平分线,
求:∠ABD的度数。
板
书
设
计
1.三角形内角和是180°。
2.几何语言叙述:
在△ABC中,∠A+∠B+∠C=180°。
教
学
反
思
