13.3实数
图片预览





文档简介
(共18张PPT)
13.3 实数
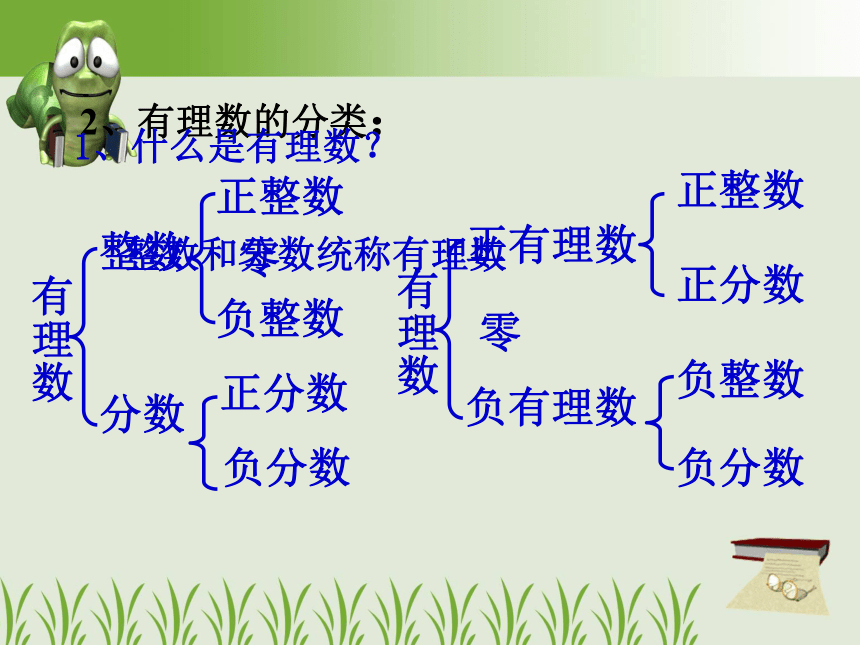
2、有理数的分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
负有理数
正整数
零
负整数
正分数
负分数
1、什么是有理数?
整数和分数统称有理数
把下列各数写成小数的形式:
有限小数
无限循环小数
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
请用计算器把 和 写成小数的形式,你有什
么发现?像这样的数我们把它叫什么数?你还
能说出一些这样的数吗?
它们都是无限不循环小数
通过前面的探讨和学习,我们知道,很多数
的_____ 根 和______根都是____________小数,
____________小数又叫无理数,
也是无理数
结论: _______和_______统称为实数
你能举出一些无理数吗
平方
立方
无限不循环
无限不循环
有理数
无理数
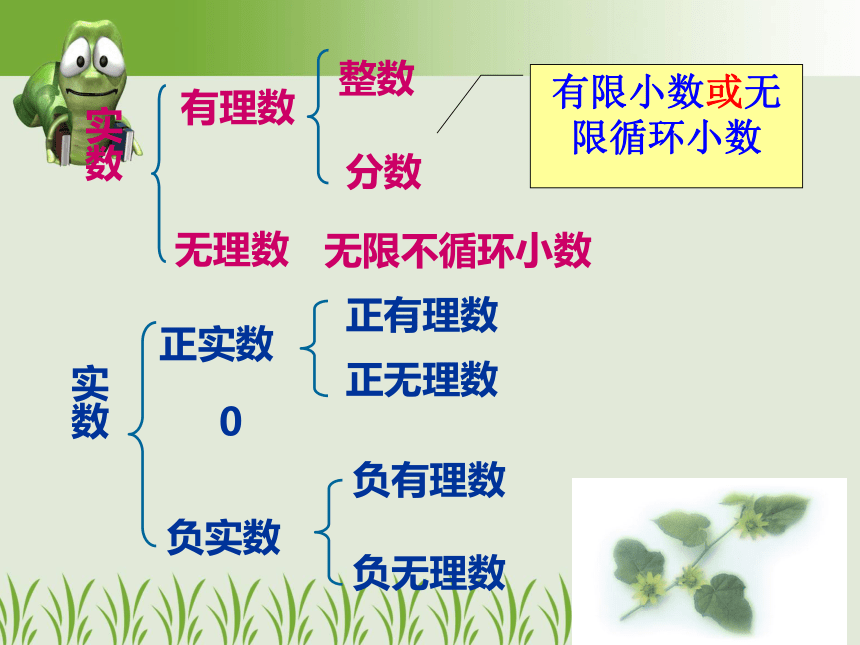
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
下列各数中,哪些是有理数,哪些是无理数?
无理数:
有理数 :
圆周率
开不尽的方根
特殊结构的数
含有无理数的一些式子
探究
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
问题2.你能在数轴上表示出 吗?
问题1.无理数能在数轴上表示出来吗?
探究
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
学以致用
1.如图,数轴上点P表示的数可能是( )
A B C D
0
-2
4
-1
1
2
3
-3
P
-3.2
2.如下图,数轴上表示 的点是______
3.假设上图中的A、B、C三个点都表示无理数,其中最小的无理数可能是_____
0
-2
4
-1
1
2
3
5
A
B
C
B
B
A
(1) 的相反数是_________, 的绝对值是__________。
(2) 的相反数是_________, 的绝对值是__________。
(1)2的相反数是__________,2的绝对值是___________。
(2)-3的相反数是_________,-3的绝对值是___________。
-2
2
3
3
在实数范围内,相反数、绝对值的意义和有理数范围内的相反数、绝对值的意义完全一样。
a是一个实数,它的相反数为 -a
0的相反数是_______
的相反数是_______
的相反数是_______
一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;0的绝对值是0
的相反数是________;
的相反数是________;
的相反数是________;
的相反数是________;
随堂练习
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
×
×
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)实数集合:
通过今天的学习,
用你自己的话说说你的收获和体会
课后作业:
P86习题13.3
第2、3题
13.3 实数
2、有理数的分类:
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
负有理数
正整数
零
负整数
正分数
负分数
1、什么是有理数?
整数和分数统称有理数
把下列各数写成小数的形式:
有限小数
无限循环小数
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
请用计算器把 和 写成小数的形式,你有什
么发现?像这样的数我们把它叫什么数?你还
能说出一些这样的数吗?
它们都是无限不循环小数
通过前面的探讨和学习,我们知道,很多数
的_____ 根 和______根都是____________小数,
____________小数又叫无理数,
也是无理数
结论: _______和_______统称为实数
你能举出一些无理数吗
平方
立方
无限不循环
无限不循环
有理数
无理数
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
下列各数中,哪些是有理数,哪些是无理数?
无理数:
有理数 :
圆周率
开不尽的方根
特殊结构的数
含有无理数的一些式子
探究
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则点A的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
无理数 可以用数轴上的点来表示.
A
问题2.你能在数轴上表示出 吗?
问题1.无理数能在数轴上表示出来吗?
探究
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
学以致用
1.如图,数轴上点P表示的数可能是( )
A B C D
0
-2
4
-1
1
2
3
-3
P
-3.2
2.如下图,数轴上表示 的点是______
3.假设上图中的A、B、C三个点都表示无理数,其中最小的无理数可能是_____
0
-2
4
-1
1
2
3
5
A
B
C
B
B
A
(1) 的相反数是_________, 的绝对值是__________。
(2) 的相反数是_________, 的绝对值是__________。
(1)2的相反数是__________,2的绝对值是___________。
(2)-3的相反数是_________,-3的绝对值是___________。
-2
2
3
3
在实数范围内,相反数、绝对值的意义和有理数范围内的相反数、绝对值的意义完全一样。
a是一个实数,它的相反数为 -a
0的相反数是_______
的相反数是_______
的相反数是_______
一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;0的绝对值是0
的相反数是________;
的相反数是________;
的相反数是________;
的相反数是________;
随堂练习
一、判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。( )
4.带根号的数都是无理数。( )
5.无理数一定都带根号。( )
6.两个无理数之积不一定是无理数。( )
×
×
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)实数集合:
通过今天的学习,
用你自己的话说说你的收获和体会
课后作业:
P86习题13.3
第2、3题
