北师大版八年级上册数学教案:5.7用二元一次方程组确定一次函数的表达式
文档属性
| 名称 | 北师大版八年级上册数学教案:5.7用二元一次方程组确定一次函数的表达式 |

|
|
| 格式 | zip | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:00:00 | ||
图片预览


文档简介
《用二元一次方程组确定一次函数的表达式》教学设计
课
题
《用二元一次方程组确定一次函数的表达式》
课型
新授课
课时
1
教
材
分
析
《用二元一次方程组确定一次函数表达式》是北师大版八年级(上)第五章《二元一次方程组》第七节,本节内容安排了1个学时完成.主要是通过对作图像方法与代数方法的比较,探索利用二元一次方程组确定一次函数的表达式.这一内容是上一课时内容的自然发展,上一课时探索了函数与方程之间的关系,并获得了方程组的图像解法,本节课研究利用二元一次方程组确定一次函数的表达式,这样更为全面地理解函数与方程、图形与代数表达式之间的关系,从而发展学生数形结合的意识。
学
情
分
析
学生已经熟练掌握了二元一次方程组的解法,同时在学习了确定一次函数的表达式的基本方法,在上一节课又学习了二元一次方程组的图像解法,这些知识为本节课的学习作好了很好的铺垫.由于上节课的惯性,学生易在图像法上停留,因为图像法很直观,容易接受,因此本节课对代数方法的渗透应有一个循序渐进的过程.
教学目标
知识与技能:
掌握利用二元一次方程组用待定系数法确定一次函数的表达式,进一步理解方程与函数的联系
过程与方法:理解作函数图像的方法与代数方法各自的特点。
情感态度与价值观:进一步理解方程与函数的联系,体会知识之间的普遍联系和知识之间的相互转化。
教学重点
利用二元一次方程组确定一次函数的表达式.
教学难点
利用二元一次方程组解决一次函数的实际问题。
教学方法
教法:激趣导入法
启发引导与自主探究相结合.
学法:合作探究法
教具准备
PPT
教
学
过
程
教学环节
教
师
活
动
预设学生活动
设计理念
激趣导入
PPT展示俄罗斯苏—24被击落事件的全过程。请大家欣赏这段视频,明白我们的数学知识在生活中随处可见。
在学生看完视频后,就土耳其的导弹击中苏—24这一过程设计问题。
观看视频,猜测观看视频的目地
激发学生学习本节课的兴趣,调动学生学习的热情
,通过对这一视频的观看,考查他们解决实际问题的能力。
初步感知
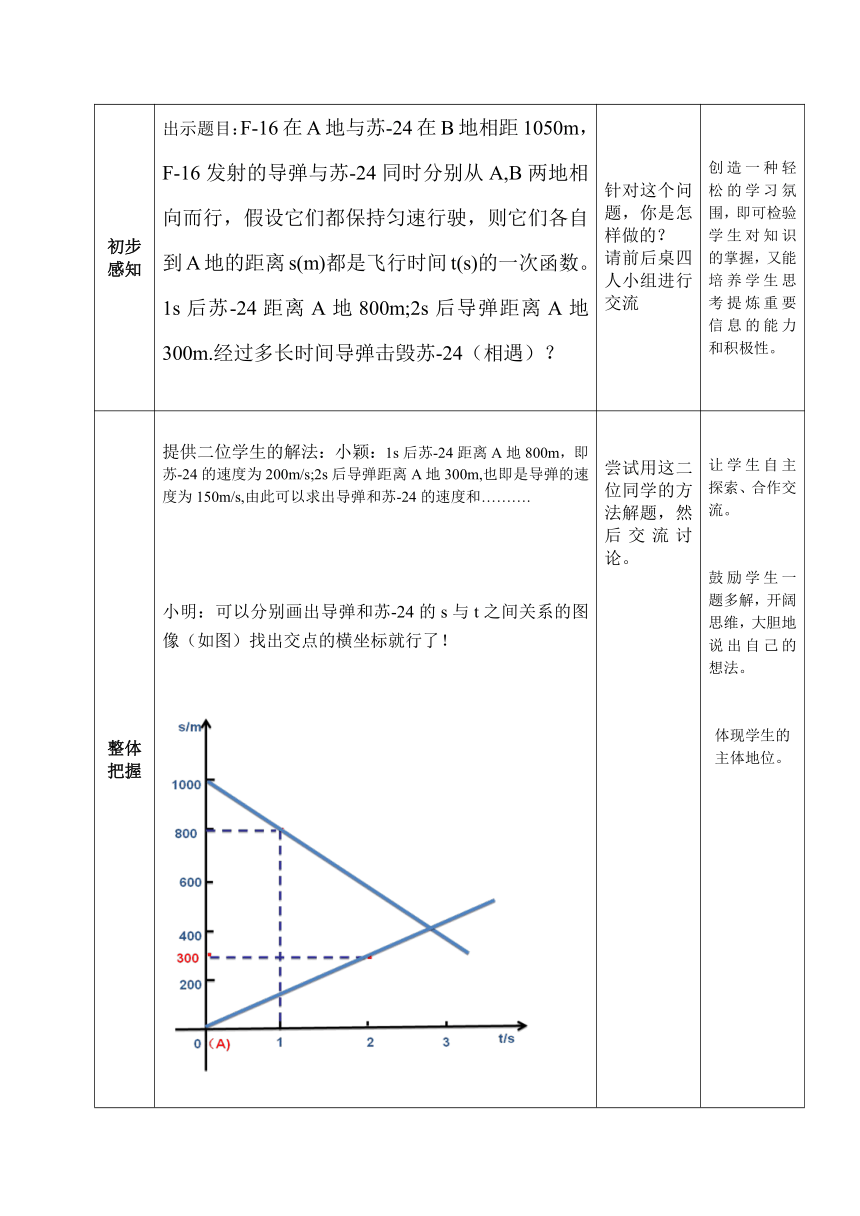
出示题目:F-16在A地与苏-24在B地相距1050m,F-16发射的导弹与苏-24同时分别从A,B两地相向而行,假设它们都保持匀速行驶,则它们各自到A地的距离s(m)都是飞行时间t(s)的一次函数。1s后苏-24距离A地800m;2s后导弹距离A地300m.经过多长时间导弹击毁苏-24(相遇)?
针对这个问题,你是怎样做的?
请前后桌四人小组进行交流
创造一种轻松的学习氛围,即可检验学生对知识的掌握,又能培养学生思考提炼重要信息的能力和积极性。
整体把握
提供二位学生的解法:小颖:1s后苏-24距离A地800m,即苏-24的速度为200m/s;2s后导弹距离A地300m,也即是导弹的速度为150m/s,由此可以求出导弹和苏-24的速度和……….
小明:可以分别画出导弹和苏-24的s与t之间关系的图像(如图)找出交点的横坐标就行了!
尝试用这二位同学的方法解题,然后交流讨论。
让学生自主探索、合作交流。
鼓励学生一题多解,开阔思维,大胆地说出自己的想法。
体现学生的主体地位。
典型例题,探究一次函数解析式的确定
例1、某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(千克)的一次函数.现知李明带了60千克的行李,交了行李费5元,张华带了90千克的行李,交了行李费10元.
写出y与x之间的函数表达式;
旅客最多可免费携带多少千克的行李?
解:(1)设,根据题意
可得方程组
解该方程组,得
所以
(2)当x=30时,y=0.
所以旅客最多可免费携带30千克的行李
像本例这样,先设出函数表达式(y=kx+b),再根据所给条件确定表达式中未知的系数(k,b的值),从而得到函数表达式的方法,叫作:待定系数法
为方便记忆,我们把待定系数法可简化为:“一设,二列,三解,四定”:
一设:设出函数表达式(y=kx+b);
二列:根据已知两点的坐标列出关于k,b的
二元一次方程组;
三解:解这个二元一次方程组,求出k,b的值;
四定:把求得的k,b的值代入y=kx+b,得出函数的关系式
在前面讨论的基础上,已有一定的能力,在合作交流中完成。
通过一个例题的探索,让学生掌握利用二元一次方程组确定一次函数的表达式的方法;在设计本例题时,考虑到,利用文字提供的信息的重要性。
归纳思考
像本例这样,先设出函数表达式(y=kx+b),再根据所给条件确定表达式中未知的系数(k,b的值),从而得到函数表达式的方法,叫作:待定系数法
为方便记忆,我们把待定系数法可简化为:“一设,二列,三解,四定”:
一设:设出函数表达式(y=kx+b);
二列:根据已知两点的坐标列出关于k,b的
二元一次方程组;
三解:解这个二元一次方程组,求出k,b的值;
四定:把求得的k,b的值代入y=kx+b,得出函数的关系式
独立思考
得出结论
学生以后能熟练引用此知识点
课堂练笔
1、一条直线交X轴于A(0,2),交Y轴于B(3,0),求着一条直线的表达式。
学生按时完成,2-3名同学当堂展示,其他同学可进行点评。
通过精选的练习题和设计启发式的问题来让学生进行训练,实现知识的有效运用。让学生在交流中进步,体验成就感,是学生的主体地位的真正体现。
课堂练笔
2某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
分别写出当0≤x≤15和x>15时,y与x的函数关系式;
若某用户十月份用水量为10吨,则应交水费多少元?若该用户十一月份交了51元的水费,则他该月用水多少吨?
解:(1)当0≤x≤15时,设,根据题意得
,解
所以当0≤x≤15时,;
当x>15时,设,根据题意,
可得方程组
解这个方程组,得
所以当x>15时,.
(2)当x=10时,代入中,得y=18.
当y=51时,代入中,得x=25.
学生按时完成,2-3名同学当堂展示,其他同学可进行点评。
通过精选的练习题和设计启发式的问题来让学生进行训练,实现知识的有效运用。让学生在交流中进步,体验成就感,是学生的主体地位的真正体现。
课堂小结
我们今天的主要目标是学会利用二元一次方程组求一次函数的表达式,通过“系数待定法”来实现这个目的!“系数待定法”的一般步骤要记牢并学会应用!
回顾学过的知识,加深理解
使学生进一步明确本节课的知识要点,锻炼学生的表达能力。
布置作业
作业:P128,习题5.8,1、2题.
板书设计
用二元一次方程组确定一次函数的表达式
图像方法与代数方法各自的特点:
利用二元一次方程组求一次函数表达式的一般步骤:
(1)
(2)
(3)
(4))
例1
课
题
《用二元一次方程组确定一次函数的表达式》
课型
新授课
课时
1
教
材
分
析
《用二元一次方程组确定一次函数表达式》是北师大版八年级(上)第五章《二元一次方程组》第七节,本节内容安排了1个学时完成.主要是通过对作图像方法与代数方法的比较,探索利用二元一次方程组确定一次函数的表达式.这一内容是上一课时内容的自然发展,上一课时探索了函数与方程之间的关系,并获得了方程组的图像解法,本节课研究利用二元一次方程组确定一次函数的表达式,这样更为全面地理解函数与方程、图形与代数表达式之间的关系,从而发展学生数形结合的意识。
学
情
分
析
学生已经熟练掌握了二元一次方程组的解法,同时在学习了确定一次函数的表达式的基本方法,在上一节课又学习了二元一次方程组的图像解法,这些知识为本节课的学习作好了很好的铺垫.由于上节课的惯性,学生易在图像法上停留,因为图像法很直观,容易接受,因此本节课对代数方法的渗透应有一个循序渐进的过程.
教学目标
知识与技能:
掌握利用二元一次方程组用待定系数法确定一次函数的表达式,进一步理解方程与函数的联系
过程与方法:理解作函数图像的方法与代数方法各自的特点。
情感态度与价值观:进一步理解方程与函数的联系,体会知识之间的普遍联系和知识之间的相互转化。
教学重点
利用二元一次方程组确定一次函数的表达式.
教学难点
利用二元一次方程组解决一次函数的实际问题。
教学方法
教法:激趣导入法
启发引导与自主探究相结合.
学法:合作探究法
教具准备
PPT
教
学
过
程
教学环节
教
师
活
动
预设学生活动
设计理念
激趣导入
PPT展示俄罗斯苏—24被击落事件的全过程。请大家欣赏这段视频,明白我们的数学知识在生活中随处可见。
在学生看完视频后,就土耳其的导弹击中苏—24这一过程设计问题。
观看视频,猜测观看视频的目地
激发学生学习本节课的兴趣,调动学生学习的热情
,通过对这一视频的观看,考查他们解决实际问题的能力。
初步感知
出示题目:F-16在A地与苏-24在B地相距1050m,F-16发射的导弹与苏-24同时分别从A,B两地相向而行,假设它们都保持匀速行驶,则它们各自到A地的距离s(m)都是飞行时间t(s)的一次函数。1s后苏-24距离A地800m;2s后导弹距离A地300m.经过多长时间导弹击毁苏-24(相遇)?
针对这个问题,你是怎样做的?
请前后桌四人小组进行交流
创造一种轻松的学习氛围,即可检验学生对知识的掌握,又能培养学生思考提炼重要信息的能力和积极性。
整体把握
提供二位学生的解法:小颖:1s后苏-24距离A地800m,即苏-24的速度为200m/s;2s后导弹距离A地300m,也即是导弹的速度为150m/s,由此可以求出导弹和苏-24的速度和……….
小明:可以分别画出导弹和苏-24的s与t之间关系的图像(如图)找出交点的横坐标就行了!
尝试用这二位同学的方法解题,然后交流讨论。
让学生自主探索、合作交流。
鼓励学生一题多解,开阔思维,大胆地说出自己的想法。
体现学生的主体地位。
典型例题,探究一次函数解析式的确定
例1、某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(千克)的一次函数.现知李明带了60千克的行李,交了行李费5元,张华带了90千克的行李,交了行李费10元.
写出y与x之间的函数表达式;
旅客最多可免费携带多少千克的行李?
解:(1)设,根据题意
可得方程组
解该方程组,得
所以
(2)当x=30时,y=0.
所以旅客最多可免费携带30千克的行李
像本例这样,先设出函数表达式(y=kx+b),再根据所给条件确定表达式中未知的系数(k,b的值),从而得到函数表达式的方法,叫作:待定系数法
为方便记忆,我们把待定系数法可简化为:“一设,二列,三解,四定”:
一设:设出函数表达式(y=kx+b);
二列:根据已知两点的坐标列出关于k,b的
二元一次方程组;
三解:解这个二元一次方程组,求出k,b的值;
四定:把求得的k,b的值代入y=kx+b,得出函数的关系式
在前面讨论的基础上,已有一定的能力,在合作交流中完成。
通过一个例题的探索,让学生掌握利用二元一次方程组确定一次函数的表达式的方法;在设计本例题时,考虑到,利用文字提供的信息的重要性。
归纳思考
像本例这样,先设出函数表达式(y=kx+b),再根据所给条件确定表达式中未知的系数(k,b的值),从而得到函数表达式的方法,叫作:待定系数法
为方便记忆,我们把待定系数法可简化为:“一设,二列,三解,四定”:
一设:设出函数表达式(y=kx+b);
二列:根据已知两点的坐标列出关于k,b的
二元一次方程组;
三解:解这个二元一次方程组,求出k,b的值;
四定:把求得的k,b的值代入y=kx+b,得出函数的关系式
独立思考
得出结论
学生以后能熟练引用此知识点
课堂练笔
1、一条直线交X轴于A(0,2),交Y轴于B(3,0),求着一条直线的表达式。
学生按时完成,2-3名同学当堂展示,其他同学可进行点评。
通过精选的练习题和设计启发式的问题来让学生进行训练,实现知识的有效运用。让学生在交流中进步,体验成就感,是学生的主体地位的真正体现。
课堂练笔
2某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
分别写出当0≤x≤15和x>15时,y与x的函数关系式;
若某用户十月份用水量为10吨,则应交水费多少元?若该用户十一月份交了51元的水费,则他该月用水多少吨?
解:(1)当0≤x≤15时,设,根据题意得
,解
所以当0≤x≤15时,;
当x>15时,设,根据题意,
可得方程组
解这个方程组,得
所以当x>15时,.
(2)当x=10时,代入中,得y=18.
当y=51时,代入中,得x=25.
学生按时完成,2-3名同学当堂展示,其他同学可进行点评。
通过精选的练习题和设计启发式的问题来让学生进行训练,实现知识的有效运用。让学生在交流中进步,体验成就感,是学生的主体地位的真正体现。
课堂小结
我们今天的主要目标是学会利用二元一次方程组求一次函数的表达式,通过“系数待定法”来实现这个目的!“系数待定法”的一般步骤要记牢并学会应用!
回顾学过的知识,加深理解
使学生进一步明确本节课的知识要点,锻炼学生的表达能力。
布置作业
作业:P128,习题5.8,1、2题.
板书设计
用二元一次方程组确定一次函数的表达式
图像方法与代数方法各自的特点:
利用二元一次方程组求一次函数表达式的一般步骤:
(1)
(2)
(3)
(4))
例1
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
