北师大版九年级数学上册1.2矩形的性质与判定第一课时矩形的性质学案(无答案)
文档属性
| 名称 | 北师大版九年级数学上册1.2矩形的性质与判定第一课时矩形的性质学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 229.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 23:15:10 | ||
图片预览


文档简介
第三讲
矩形的性质
菱形的定义是什么?
答:
2.菱形的性质
菱形的判定
自主探究
1.拿一个可以活动的平行四边形教具,轻轻拉动一个点并观察,它还是一个平行四边形吗?为什么?(演示拉动过程如图)
2.再次演示平行四边形的移动过程,当移动到一个角是直角时停止,让学生观察这是什么图形.
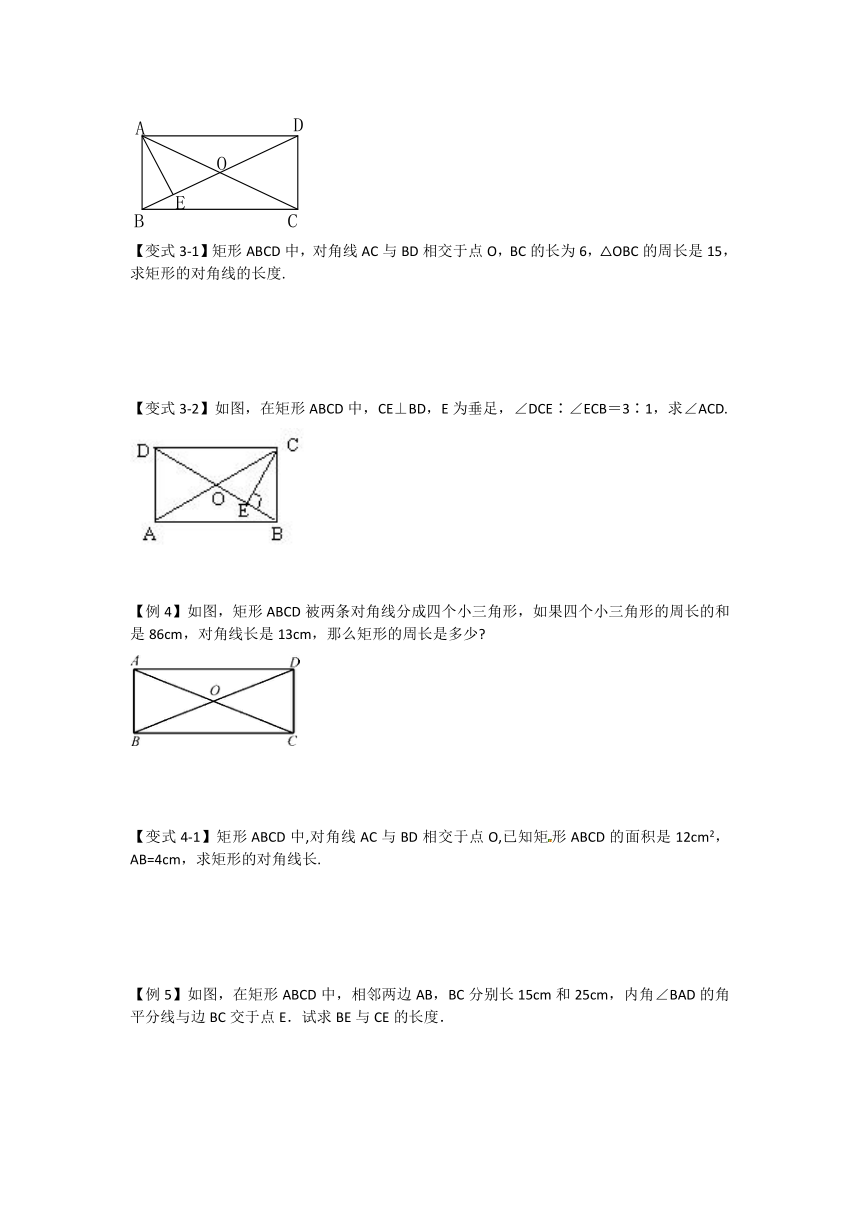
归纳结论:矩形定义:
3.学生观察教师的教具,研究其变化情况后,可以发现:矩形是平行四边形的特例,属于平行四边形,因此它具有平行四边形所有性质.
思考:矩形还具有哪些特殊的性质?为什么?
归纳结论:
矩形性质1:矩形的四个角都是
矩形性质2:矩形的对角线
4.矩形是轴对称图形吗?如果是,它有几条对称轴?
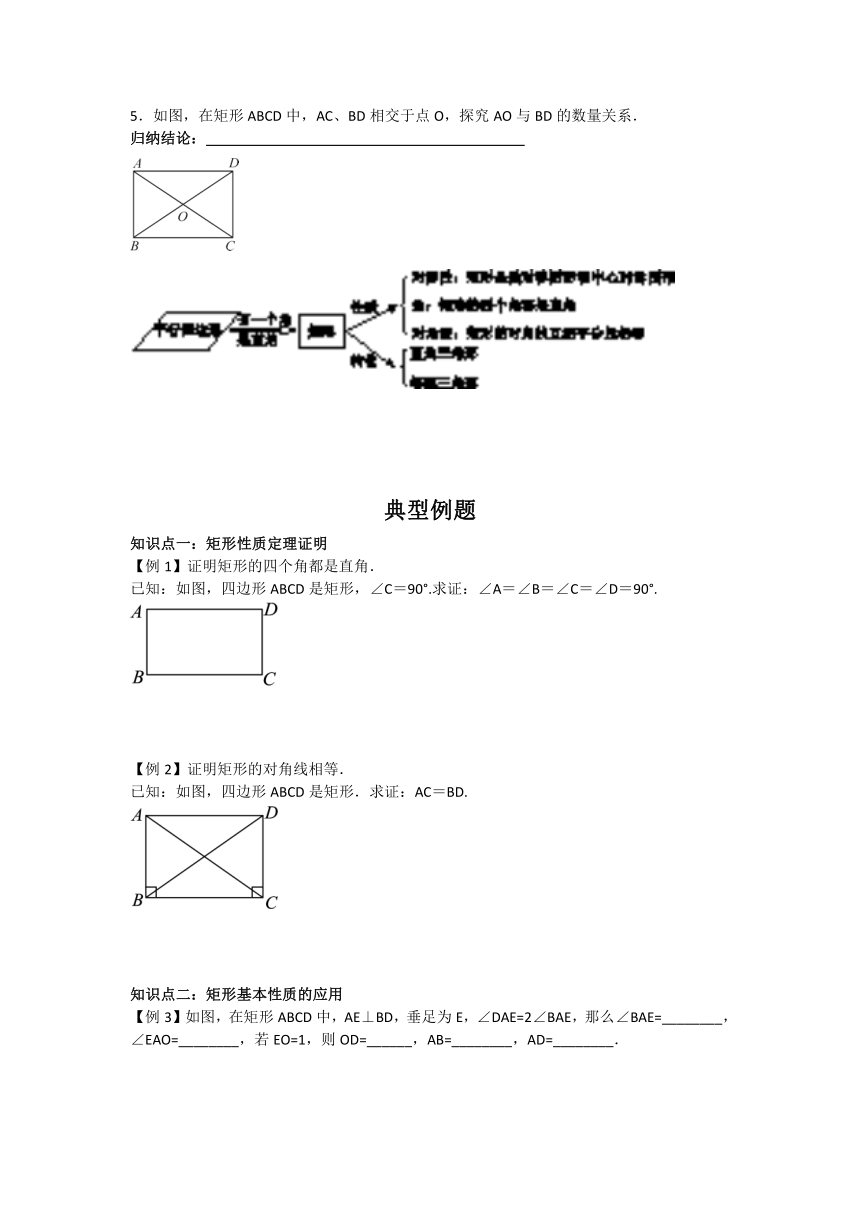
5.如图,在矩形ABCD中,AC、BD相交于点O,探究AO与BD的数量关系.
归纳结论:
典型例题
知识点一:矩形性质定理证明
【例1】证明矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,∠C=90°.求证:∠A=∠B=∠C=∠D=90°.
【例2】证明矩形的对角线相等.
已知:如图,四边形ABCD是矩形.求证:AC=BD.
知识点二:矩形基本性质的应用
【例3】如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,那么∠BAE=________,∠EAO=________,若EO=1,则OD=______,AB=________,AD=________.
【变式3-1】矩形ABCD中,对角线AC与BD相交于点O,BC的长为6,△OBC的周长是15,求矩形的对角线的长度.
【变式3-2】如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE∶∠ECB=3∶1,求∠ACD.
【例4】如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
【变式4-1】矩形ABCD中,对角线AC与BD相交于点O,已知矩形ABCD的面积是12cm2,AB=4cm,求矩形的对角线长.
【例5】如图,在矩形ABCD中,相邻两边AB,BC分别长15cm和25cm,内角∠BAD的角平分线与边BC交于点E.试求BE与CE的长度.
【变式5-1】如图,在矩形ABCD中,E是边AD上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.
【例6】如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
知识点三:等面积法
【例7】如图,在矩形ABCD中,AB=3,
BC=4,
BE⊥AC于E.试求出BE的长.
【变式7-1】如图,矩形ABCD中,E点在BC上,且AE平分∠BAC.
若BE=4,AC
=15,则△AEC面积为(
)
A.15
B.
30
C.
45
D.
60
【变式7-2】:如图:在矩形ABCD中,两条对角线AC,BD相交于点O,AB=4cm
,AD=cm.
(1)判定△AOB的形状.
(2)计算△BOC的面积.
【变式7-3】如图,将矩形ABCD沿着直线BD折叠使点C落在点
C'处,BC'交AD于E,AD=8,AB=4,BE=5,求△BED的面积.
【例8】如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,则PE+PF等于
.
知识点四:矩形对角线平分且相等
【例9】矩形的两条对角线相交成60°角,较短边与一条对角线之和为15cm
,则矩形的对角线长为
cm.
【变式9-1】矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是(
)
A.57.5°
B.32.5°
C.57.5°,
33.5°
D.57.5°,32.5°
【变式9-2】矩形两条对角线的夹角是120°,短边长4cm;则矩形的对角线长
.
【变式9-3】如图,矩形ABCD的对角线相交于点O,∠AOD=120°,AD=5cm,则AC=
.
知识点五:直角三角形斜边上的中线等于斜边的一半
【例10】如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为________.
【变式10-1】如图,在△ABC中,D,E,F分别为BC,AC,AB的中点,AH⊥BC于点H,FD=8cm,则HE的值为
【变式10-2】已知一个直角三角形斜边上的中线长为6cm,那么这个直角三角形的斜边长为______cm.
知识点七:折叠问题
【例11】如图,将矩形ABCD沿对角线AC翻折,点B落在点E处,FC交AD于F.
(1)求证:△AFE≌△CFD;
(2)若AB=4,BC=8,求图中阴影部分的面积.
【变式12-1】如图,长方形纸片ABCD沿对角线AC折叠,设点D落在D′处,BC交AD′于点E,AB=6cm,BC=8cm,求阴影部分的面积.
【变式12-2】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是
【变式12-3】将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为
课堂训练
A组
1.
已知四边形ABCD,若AB∥CD,AD∥BC,且∠A=90°,则四边形ABCD为____________.
2.下列命题是假命题的是( )
A.矩形的对角线相等
B.矩形的对边相等
C.矩形的对角线互相平分
D.矩形的对角线互相垂直
3.如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是(
)
A.30°
B.60°
C.90°
D.120°
第3题图
第4题图
第5题图
4.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )
A.∠ABC=90°
B.AC=BD
C.OA=OB
D.OA=AD
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为( )
A.4
B.3
C.2
D.1
6.如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是( )
A.8
B.6
C.4
D.2
第6题图
第7题图
第8题图
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,求AC的长.
8.如图,在矩形ABCD中,点E.
F分别是边AB,CD的中点.求证:DE=BF.
B组
1.如图,在Rt△ABC中,∠ACB=90°,AB=10
cm,D为AB的中点,则CD=____________cm.
第1题图
第2题图
第3题图
2.如图所示,一根长a
m的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.请判断木棍滑动的过程中,点P到点O的距离____________(填“发生”或“不发生”)变化.
3.如图,在矩形ABCD中,对角线AC与BD相交于点O,且AB=OA=2
cm,则AD的长为____________.
4.已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G,H,连接EH,FG.
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
1.如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
A.14
B.16
C.17
D.18
第1题图
第2题图
第3题图
2.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD,AC于点E,O,连接CE,则CE的长为( )
A.3
B.3.5
C.2.5
D.2.8
3.如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为____________.
4.如图,在矩形ABCD中,=,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE·ED=,则矩形ABCD的面积为____________.
5.如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.求证:DF=DC.
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.
矩形的性质
菱形的定义是什么?
答:
2.菱形的性质
菱形的判定
自主探究
1.拿一个可以活动的平行四边形教具,轻轻拉动一个点并观察,它还是一个平行四边形吗?为什么?(演示拉动过程如图)
2.再次演示平行四边形的移动过程,当移动到一个角是直角时停止,让学生观察这是什么图形.
归纳结论:矩形定义:
3.学生观察教师的教具,研究其变化情况后,可以发现:矩形是平行四边形的特例,属于平行四边形,因此它具有平行四边形所有性质.
思考:矩形还具有哪些特殊的性质?为什么?
归纳结论:
矩形性质1:矩形的四个角都是
矩形性质2:矩形的对角线
4.矩形是轴对称图形吗?如果是,它有几条对称轴?
5.如图,在矩形ABCD中,AC、BD相交于点O,探究AO与BD的数量关系.
归纳结论:
典型例题
知识点一:矩形性质定理证明
【例1】证明矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,∠C=90°.求证:∠A=∠B=∠C=∠D=90°.
【例2】证明矩形的对角线相等.
已知:如图,四边形ABCD是矩形.求证:AC=BD.
知识点二:矩形基本性质的应用
【例3】如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,那么∠BAE=________,∠EAO=________,若EO=1,则OD=______,AB=________,AD=________.
【变式3-1】矩形ABCD中,对角线AC与BD相交于点O,BC的长为6,△OBC的周长是15,求矩形的对角线的长度.
【变式3-2】如图,在矩形ABCD中,CE⊥BD,E为垂足,∠DCE∶∠ECB=3∶1,求∠ACD.
【例4】如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
【变式4-1】矩形ABCD中,对角线AC与BD相交于点O,已知矩形ABCD的面积是12cm2,AB=4cm,求矩形的对角线长.
【例5】如图,在矩形ABCD中,相邻两边AB,BC分别长15cm和25cm,内角∠BAD的角平分线与边BC交于点E.试求BE与CE的长度.
【变式5-1】如图,在矩形ABCD中,E是边AD上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.
【例6】如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
知识点三:等面积法
【例7】如图,在矩形ABCD中,AB=3,
BC=4,
BE⊥AC于E.试求出BE的长.
【变式7-1】如图,矩形ABCD中,E点在BC上,且AE平分∠BAC.
若BE=4,AC
=15,则△AEC面积为(
)
A.15
B.
30
C.
45
D.
60
【变式7-2】:如图:在矩形ABCD中,两条对角线AC,BD相交于点O,AB=4cm
,AD=cm.
(1)判定△AOB的形状.
(2)计算△BOC的面积.
【变式7-3】如图,将矩形ABCD沿着直线BD折叠使点C落在点
C'处,BC'交AD于E,AD=8,AB=4,BE=5,求△BED的面积.
【例8】如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,则PE+PF等于
.
知识点四:矩形对角线平分且相等
【例9】矩形的两条对角线相交成60°角,较短边与一条对角线之和为15cm
,则矩形的对角线长为
cm.
【变式9-1】矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是(
)
A.57.5°
B.32.5°
C.57.5°,
33.5°
D.57.5°,32.5°
【变式9-2】矩形两条对角线的夹角是120°,短边长4cm;则矩形的对角线长
.
【变式9-3】如图,矩形ABCD的对角线相交于点O,∠AOD=120°,AD=5cm,则AC=
.
知识点五:直角三角形斜边上的中线等于斜边的一半
【例10】如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为________.
【变式10-1】如图,在△ABC中,D,E,F分别为BC,AC,AB的中点,AH⊥BC于点H,FD=8cm,则HE的值为
【变式10-2】已知一个直角三角形斜边上的中线长为6cm,那么这个直角三角形的斜边长为______cm.
知识点七:折叠问题
【例11】如图,将矩形ABCD沿对角线AC翻折,点B落在点E处,FC交AD于F.
(1)求证:△AFE≌△CFD;
(2)若AB=4,BC=8,求图中阴影部分的面积.
【变式12-1】如图,长方形纸片ABCD沿对角线AC折叠,设点D落在D′处,BC交AD′于点E,AB=6cm,BC=8cm,求阴影部分的面积.
【变式12-2】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是
【变式12-3】将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为
课堂训练
A组
1.
已知四边形ABCD,若AB∥CD,AD∥BC,且∠A=90°,则四边形ABCD为____________.
2.下列命题是假命题的是( )
A.矩形的对角线相等
B.矩形的对边相等
C.矩形的对角线互相平分
D.矩形的对角线互相垂直
3.如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是(
)
A.30°
B.60°
C.90°
D.120°
第3题图
第4题图
第5题图
4.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是( )
A.∠ABC=90°
B.AC=BD
C.OA=OB
D.OA=AD
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为( )
A.4
B.3
C.2
D.1
6.如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是( )
A.8
B.6
C.4
D.2
第6题图
第7题图
第8题图
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,求AC的长.
8.如图,在矩形ABCD中,点E.
F分别是边AB,CD的中点.求证:DE=BF.
B组
1.如图,在Rt△ABC中,∠ACB=90°,AB=10
cm,D为AB的中点,则CD=____________cm.
第1题图
第2题图
第3题图
2.如图所示,一根长a
m的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.请判断木棍滑动的过程中,点P到点O的距离____________(填“发生”或“不发生”)变化.
3.如图,在矩形ABCD中,对角线AC与BD相交于点O,且AB=OA=2
cm,则AD的长为____________.
4.已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G,H,连接EH,FG.
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
1.如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
A.14
B.16
C.17
D.18
第1题图
第2题图
第3题图
2.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD,AC于点E,O,连接CE,则CE的长为( )
A.3
B.3.5
C.2.5
D.2.8
3.如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为____________.
4.如图,在矩形ABCD中,=,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE·ED=,则矩形ABCD的面积为____________.
5.如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.求证:DF=DC.
6.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
