北师大版九年级数学上册1.3正方形的性质与判定第二课时正方形的判定学案(无答案)
文档属性
| 名称 | 北师大版九年级数学上册1.3正方形的性质与判定第二课时正方形的判定学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 213.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 23:19:49 | ||
图片预览



文档简介
正方形的判定
正方形性质定理复习
1.正方形的四个角都是
,四条边
.
2.正方形的对角线相等且
.
3.正方形的一条对角线长为4,则这个正方形的面积是(
)
A.8
B.4
C.8 D.16
1.活动内容:问题:将一长方形纸对折两次,然后剪下一个角,打开,怎样剪才能剪出一个正方形?(学生动手折叠.
思考.
剪切)
答:
2.思考:由矩形变为正方形还需要哪些条件?由菱形变为正方形还需要哪些条件?
归纳结论:
正方形的判定定理:
(1)对角线相等的菱形是正方形;
(2)有一个角是直角的菱形是正方形;
(3)对角线垂直的矩形是正方形;
(4)有一组邻边相等的矩形是正方形.
3.教师可以课件展示下面的框架图,复习巩固平行四边形,矩形,菱形,正方形之间的关系.
知识点一:正方形的判定定理的应用
【例1】四边形ABCD中,AC,BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD
B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C
D.OA=OC,OB=OD,AB=BC
【变式1-1】下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.两组对边分别相等的四边形是平行四边形
C.矩形的对角线相等
D.有一组邻边相等且有一个角是直角的四边形是正方形
【变式1-2】在下列命题中,是真命题的是( )
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相平分的四边形是平行四边形
D.两条对角线互相垂直且相等的四边形是正方形
【变式1-3】下列命题中,正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线相等的菱形是正方形
【例2】如图,在矩形
ABCD
中,BE平分∠
ABC,CE
平分∠
DCB,BF∥CE,CF∥BE.求证:四边形
BECF
是正方形.
【变式2-1】如图,在Rt△ABC中,∠ACB=90?,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F,求证:四边形CFDE是正方形.
【变式2-2】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF,FG相交于点H.
(1)判断线段DE.
FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
【变式2-3】:如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
知识点二:“添加条件”类型题目
【例3】下列条件之一能使菱形ABCD是正方形的为( )
①AC⊥BD
②∠BAD=90°
③AB=BC
④AC=BD.
A.①③
B.②③
C.②④
D.①②③
【变式3-1】已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①②
B.选②③
C.选①③
D.选②④
【变式3-2】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
【变式3-3】如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、BC的中点,连接DE、DF、EF,要使四边形DECF是正方形,只需增加一个条件为 .
【例4】如图,在△ABC中,点D.
E分别是边BC.
AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD,CF.
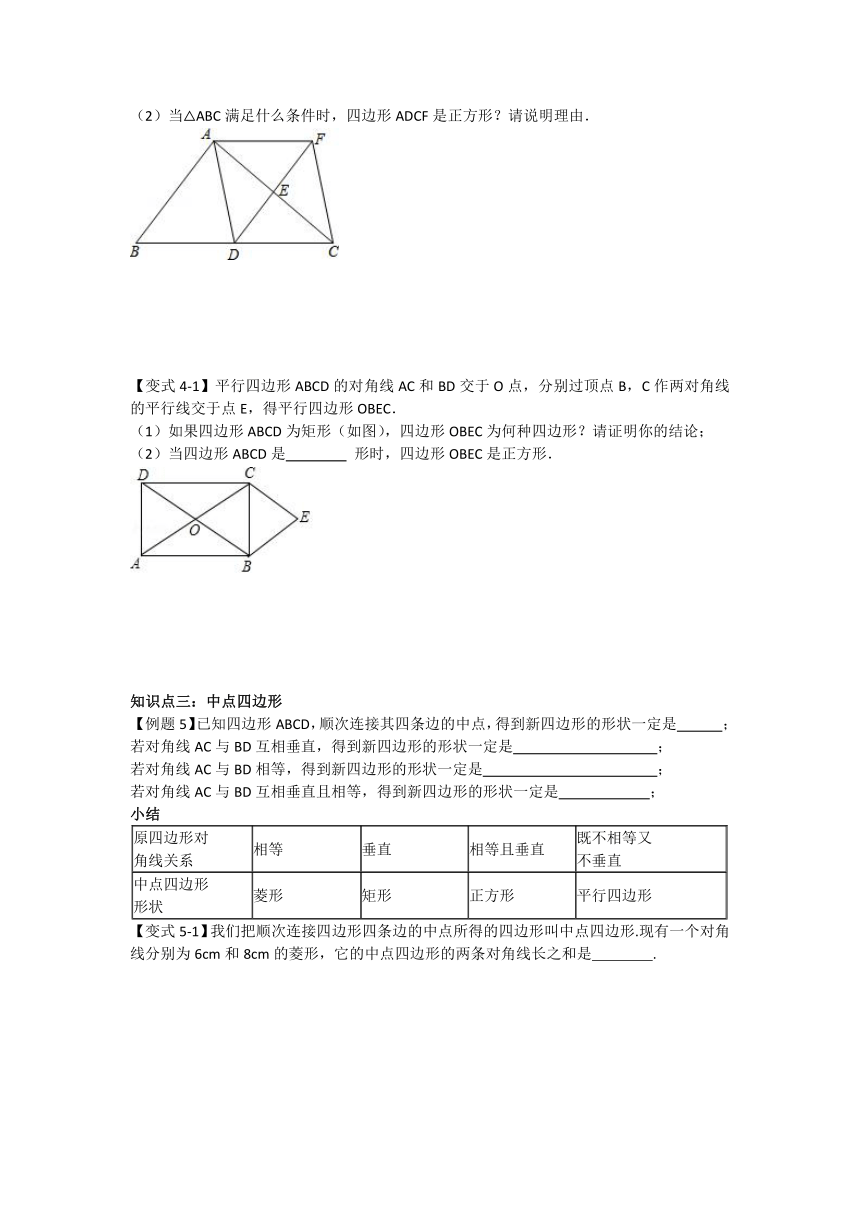
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【变式4-1】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是
形时,四边形OBEC是正方形.
知识点三:中点四边形
【例题5】已知四边形ABCD,顺次连接其四条边的中点,得到新四边形的形状一定是
;若对角线AC与BD互相垂直,得到新四边形的形状一定是
;
若对角线AC与BD相等,得到新四边形的形状一定是
;
若对角线AC与BD互相垂直且相等,得到新四边形的形状一定是
;
小结
原四边形对
角线关系
相等
垂直
相等且垂直
既不相等又
不垂直
中点四边形
形状
菱形
矩形
正方形
平行四边形
【变式5-1】我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形.现有一个对角线分别为6cm和8cm的菱形,它的中点四边形的两条对角线长之和是 .
【变式5-1】
【变式5-2】
【变式5-2】如图,已知矩形ABCD的对角线长为8cm,E,F,G,H分别是AB,BC,CD,DA的点,则四边形EFGH的周长等于
.
A组
1.下列说法不正确的是( )
A.对角线互相垂直的矩形是正方形
B.对角线相等的菱形是正方形
C.有一个角是直角的平行四边形是正方形
D.一组邻边相等的矩形是正方形
2.如图,在四边形ABCD中,对角线AC,BD相交于点O,若AO=CO=BO=DO,AC⊥BD,则四边形ABCD的形状是( )
A.平行四边形
B.矩形
C.菱形
D.正方形
3.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.∠D=90°
B.AB=CD
C.AD=BC
D.BC=CD
4.如图,将矩形纸片折叠,使A点落在BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
第4题图
第5题图
第6题图
5.小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使?ABCD成为正方形(如图).现有下列四种选法,你认为其中错误的是( )
A.①②
B.②③
C.①③
D.②④
6.如图,菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件______________,使四边形ABCD是正方形(填一个即可).
7.矩形各内角的平分线围成一个( )
A.平行四边形
B.正方形
C.矩形
D.菱形
8.如图,把一个矩形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为____________.
B组
1.如图,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连接AF与BE,CE与DF,分别交于点M,N,则四边形EMFN是( )
A.正方形
B.菱形
C.矩形
D.无法确定
第1题图
第2题图
2.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
3.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD.垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
4.已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=_________°时,四边形ACED是正方形?请说明理由.
1.正方形具有而菱形不一定具有的性质是(
)
A.内角和为360°
B.对角线相等
C.对角线平分内角
D.对角线互相垂直平分
2.正方形具有而矩形不一定具有的性质是(
)
A.四个角都相等
B.四条边相等
C.对角线相等
D.对角线互相平分
3.一个正方形和一个等腰三角形有相同的周长,等腰三角形的边长分别为5.6cm和13.2cm,则这个正方形的面积为(
)
A.24cm2
B.36cm2
C.48cm2
D.64cm2
4.如图,正方形ABCD中,点E是CD边上一点,连接AE,交对角线BD于点F,连接CF,则图中全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
第4题图
第5题图
第6题图
5.如图,E为正方形ABCD内的一点,且△BCE为等边三角形,则∠ABE=
,∠AEB=
,∠AED=
.
6.如图,已知正方形ABCD中,E为对角线AC上的一点,且AE=AB.则∠EBC的度数是
.
7.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP度数是
.
第7题图
第8题图
第9题图
8.如图,四边形ABCD为正方形,以AB为边向正方形外做等边△ABE,交BD于F,则∠AFD=
.
9.如图,正方形ABCD的周长为15cm,则矩形EFCG的周长是________.
10.如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点为中心,把△ADE顺时针旋转900,得△ABE/,连接EE/,则EE/的长等于
.
第10题图
第11题图
11.如图,正方形ABCD的面积等于9cm2,正方形DEFG的面积等于4cm2,则阴影部分的面积为多少?
12.如图,B.
C.
E是同一直线上的三个点,四边形ABCD与四边形CEFG是都是正方形.连接BG,DE,观察猜想BG与DE之间的大小关系,并证明你的结论.
13.如图,点E,F在正方形ABCD的边BC,CD上,BE=CF.
(1)AE与BF相等吗?为什么?(2)AE与BF是否垂直?说明你的理由.
14.在正方形ABCD中,E在BC上,且BE=2,EC=1,点P在BD上,求PE+PC的最小值.
正方形性质定理复习
1.正方形的四个角都是
,四条边
.
2.正方形的对角线相等且
.
3.正方形的一条对角线长为4,则这个正方形的面积是(
)
A.8
B.4
C.8 D.16
1.活动内容:问题:将一长方形纸对折两次,然后剪下一个角,打开,怎样剪才能剪出一个正方形?(学生动手折叠.
思考.
剪切)
答:
2.思考:由矩形变为正方形还需要哪些条件?由菱形变为正方形还需要哪些条件?
归纳结论:
正方形的判定定理:
(1)对角线相等的菱形是正方形;
(2)有一个角是直角的菱形是正方形;
(3)对角线垂直的矩形是正方形;
(4)有一组邻边相等的矩形是正方形.
3.教师可以课件展示下面的框架图,复习巩固平行四边形,矩形,菱形,正方形之间的关系.
知识点一:正方形的判定定理的应用
【例1】四边形ABCD中,AC,BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD
B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C
D.OA=OC,OB=OD,AB=BC
【变式1-1】下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.两组对边分别相等的四边形是平行四边形
C.矩形的对角线相等
D.有一组邻边相等且有一个角是直角的四边形是正方形
【变式1-2】在下列命题中,是真命题的是( )
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相平分的四边形是平行四边形
D.两条对角线互相垂直且相等的四边形是正方形
【变式1-3】下列命题中,正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线相等的菱形是正方形
【例2】如图,在矩形
ABCD
中,BE平分∠
ABC,CE
平分∠
DCB,BF∥CE,CF∥BE.求证:四边形
BECF
是正方形.
【变式2-1】如图,在Rt△ABC中,∠ACB=90?,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F,求证:四边形CFDE是正方形.
【变式2-2】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF,FG相交于点H.
(1)判断线段DE.
FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
【变式2-3】:如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
知识点二:“添加条件”类型题目
【例3】下列条件之一能使菱形ABCD是正方形的为( )
①AC⊥BD
②∠BAD=90°
③AB=BC
④AC=BD.
A.①③
B.②③
C.②④
D.①②③
【变式3-1】已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①②
B.选②③
C.选①③
D.选②④
【变式3-2】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
【变式3-3】如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、BC的中点,连接DE、DF、EF,要使四边形DECF是正方形,只需增加一个条件为 .
【例4】如图,在△ABC中,点D.
E分别是边BC.
AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD,CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【变式4-1】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是
形时,四边形OBEC是正方形.
知识点三:中点四边形
【例题5】已知四边形ABCD,顺次连接其四条边的中点,得到新四边形的形状一定是
;若对角线AC与BD互相垂直,得到新四边形的形状一定是
;
若对角线AC与BD相等,得到新四边形的形状一定是
;
若对角线AC与BD互相垂直且相等,得到新四边形的形状一定是
;
小结
原四边形对
角线关系
相等
垂直
相等且垂直
既不相等又
不垂直
中点四边形
形状
菱形
矩形
正方形
平行四边形
【变式5-1】我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形.现有一个对角线分别为6cm和8cm的菱形,它的中点四边形的两条对角线长之和是 .
【变式5-1】
【变式5-2】
【变式5-2】如图,已知矩形ABCD的对角线长为8cm,E,F,G,H分别是AB,BC,CD,DA的点,则四边形EFGH的周长等于
.
A组
1.下列说法不正确的是( )
A.对角线互相垂直的矩形是正方形
B.对角线相等的菱形是正方形
C.有一个角是直角的平行四边形是正方形
D.一组邻边相等的矩形是正方形
2.如图,在四边形ABCD中,对角线AC,BD相交于点O,若AO=CO=BO=DO,AC⊥BD,则四边形ABCD的形状是( )
A.平行四边形
B.矩形
C.菱形
D.正方形
3.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.∠D=90°
B.AB=CD
C.AD=BC
D.BC=CD
4.如图,将矩形纸片折叠,使A点落在BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
第4题图
第5题图
第6题图
5.小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使?ABCD成为正方形(如图).现有下列四种选法,你认为其中错误的是( )
A.①②
B.②③
C.①③
D.②④
6.如图,菱形ABCD中,对角线AC,BD相交于点O,不添加任何辅助线,请添加一个条件______________,使四边形ABCD是正方形(填一个即可).
7.矩形各内角的平分线围成一个( )
A.平行四边形
B.正方形
C.矩形
D.菱形
8.如图,把一个矩形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为____________.
B组
1.如图,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连接AF与BE,CE与DF,分别交于点M,N,则四边形EMFN是( )
A.正方形
B.菱形
C.矩形
D.无法确定
第1题图
第2题图
2.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
3.如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD.垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
4.已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=_________°时,四边形ACED是正方形?请说明理由.
1.正方形具有而菱形不一定具有的性质是(
)
A.内角和为360°
B.对角线相等
C.对角线平分内角
D.对角线互相垂直平分
2.正方形具有而矩形不一定具有的性质是(
)
A.四个角都相等
B.四条边相等
C.对角线相等
D.对角线互相平分
3.一个正方形和一个等腰三角形有相同的周长,等腰三角形的边长分别为5.6cm和13.2cm,则这个正方形的面积为(
)
A.24cm2
B.36cm2
C.48cm2
D.64cm2
4.如图,正方形ABCD中,点E是CD边上一点,连接AE,交对角线BD于点F,连接CF,则图中全等三角形共有(
)
A.1对
B.2对
C.3对
D.4对
第4题图
第5题图
第6题图
5.如图,E为正方形ABCD内的一点,且△BCE为等边三角形,则∠ABE=
,∠AEB=
,∠AED=
.
6.如图,已知正方形ABCD中,E为对角线AC上的一点,且AE=AB.则∠EBC的度数是
.
7.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP度数是
.
第7题图
第8题图
第9题图
8.如图,四边形ABCD为正方形,以AB为边向正方形外做等边△ABE,交BD于F,则∠AFD=
.
9.如图,正方形ABCD的周长为15cm,则矩形EFCG的周长是________.
10.如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点为中心,把△ADE顺时针旋转900,得△ABE/,连接EE/,则EE/的长等于
.
第10题图
第11题图
11.如图,正方形ABCD的面积等于9cm2,正方形DEFG的面积等于4cm2,则阴影部分的面积为多少?
12.如图,B.
C.
E是同一直线上的三个点,四边形ABCD与四边形CEFG是都是正方形.连接BG,DE,观察猜想BG与DE之间的大小关系,并证明你的结论.
13.如图,点E,F在正方形ABCD的边BC,CD上,BE=CF.
(1)AE与BF相等吗?为什么?(2)AE与BF是否垂直?说明你的理由.
14.在正方形ABCD中,E在BC上,且BE=2,EC=1,点P在BD上,求PE+PC的最小值.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
