第2章轴对称图形 单元复习一(基础卷)-苏科版八年级数学上册期末复习(word版含答案)
文档属性
| 名称 | 第2章轴对称图形 单元复习一(基础卷)-苏科版八年级数学上册期末复习(word版含答案) | 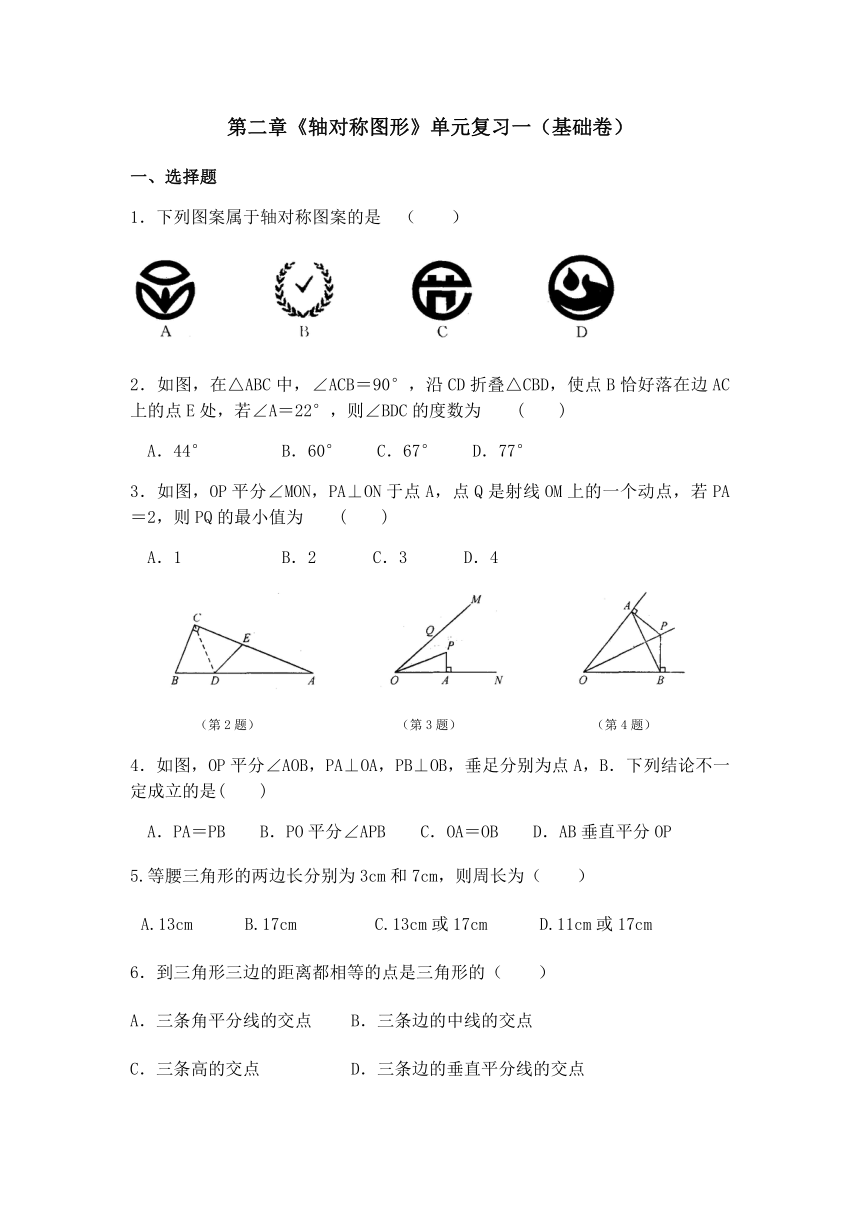 | |
| 格式 | zip | ||
| 文件大小 | 112.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 21:50:20 | ||
图片预览




文档简介
第二章《轴对称图形》单元复习一(基础卷)
一、选择题
1.下列图案属于轴对称图案的是 ( )
2.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上的点E处,若∠A=22°,则∠BDC的度数为
(
)
A.44°
B.60°
C.67°
D.77°
3.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为
(
)
A.1
B.2
C.3
D.4
(第2题)
(第3题)
(第4题)
4.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为点A,B.下列结论不一定成立的是(
)
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
5.等腰三角形的两边长分别为3cm和7cm,则周长为( )
A.13cm
B.17cm
C.13cm或17cm
D.11cm或17cm
6.到三角形三边的距离都相等的点是三角形的( )
A.三条角平分线的交点
B.三条边的中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
7.下列满足条件的三角形中,不是直角三角形的是
A.三内角之比为1:2:3
B.三边长的平方之比为1:2:3
C.三边长之比为3:4:5
D.三内角之比为3:4:5
8.已知等腰三角形的一个外角等于100°,则它的顶角是( )
A.80°
B.20°
C.80°或20°
D.不能确定
填空题
9.如图,在正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有_______种.
(第9题)
(第12题)
(第13题)
(第14题)
10.等腰三角形的周长为16,若一边长为6,则另两边的长为_______.
11.在△ABC中,∠A=400
,当∠C=
时,△ABC为等腰三角形.
12.如图,△ABC是等边三角形,D,E,F分别是AB,BC,CA边上的一点.若AD=BE=CF,则△DEF的形状是_______.
13.如图,在△ABC中,AB=AC,CD平分∠ACB,∠A=36°,则∠BDC=_______.
14.如图,在△ABC中,AB=AC,DE垂直平分AB.若BE⊥AC,AF⊥BC,垂足分别为点E,F,则么∠EFC=_______.
15.如图,△ABC中,∠C=90°,AC=3,AB=5,点D是边BC上一点.若沿AD将△ACD翻折,点C刚好落在AB边上点E处,则BD=
.
16.若直角三角形的三边分别为x,8,10,则=
.
17.已知直角三角形两边a,b满足,则斜边c上中线的长为
.
18.如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC=AD.有如下四个结论:CDAC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.请写出正确结论的序号_______.(填序号)
(第18题)
三、解答题
19.(1)已知△DEF,用直尺和圆规作点P,使点P到△DEF三边距离相等
(不写作法,保留作图痕迹).
(2)在图示的网格中,作出△ABC关于MN对称的图形△A1B1C1;
说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
20.现有9个相同的小正三角形拼成的大正三角形,将其部分涂黑.如图(1),(2)所示.观察图(1),图(2)中涂黑部分构成的图案.它们具有如下特征:①都是轴对称图形;②涂黑部分都是三个小正三角形.
请在图(3),图(4)内分别设计一个新图案,使图案具有上述两个特征.
21.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
22.如图,在△ABC中,AB=AC,D为边BC上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)求证:DC=AB.
23.如图,在△ABC中,AB=AC,BE平分∠ABC,DE∥BC,交AC于点D.
(1)求证:BD=DE;
(2)若∠DEB=30°且DE=3,求AD的长度.
24.如图,在△ABC中,CD是AB边上的高,BE是AC边上的中线,
BD=CE.
(1)求证:点D在BE的垂直平分线上;
(2)若∠ABE
=25°,求∠BEC的度数.
25.如图,在△ABC中,∠A=70°,BP是∠ABC的平分线,CP是∠ACD的平分线.
(1)如图1,求∠P的度数;
(2)如图2,过点P作EF∥BC,分别与边AB,AC交于点E,F,判断线段BE,EF,CF之间的数_______.量关系,并说明理由.
26.【感知】
如图1,在四边形ABCD中,∠C=∠ADC=90°,点E在边CD,且满足△AEB是等腰直角三角形,∠AEB=90°.求证:△ADE≌△ECB.
【探究】
如图2,在四边形ABCD中,∠C=∠ADC=90°,点E在边CD,且满足△AEB是等腰直角三角形,∠AEB=90°,点F在边AD的延长线上,连接EF,以EF为直角边作等腰Rt△EFG,过点G作GT⊥CD,垂足为T,连接BG交CD于点H.
求证:BH=GH.
【拓展】
如图3,点E在四边形ABCD内,∠AEB+∠DEC=180°,且AE=BE,DE=CE,过点E作EF交AD于点F,使∠EFA=∠AEB,延长FE交BC于点G.试探究BG与BC之间的数量关系,并说明理由.
第二章《轴对称图形》单元复习一(基础卷)
参考答案
一、选择题
1.A
2.C
3.B
4.D
5.B
6.A
7.D
8.C
二、填空题
9.3
10.5,5或6,4
11
40或70或
100°
12.等边三角形
13.72°
14.45°15.2.5
16.
36或164
17.4或5
18.①③
三、解答题
19.
(1)分别作两条角平分线交于点P,作出△A1B1C1,
(2)将它先向右平移6格,再向下平移2格得到△A2B2C
20.解:如图
21.(1)15cm
(2)40°
22.(1)
∵AB=AC,
∴∠B=∠C=30°,
∵∠C
+∠BAC+∠B=180°,
∴∠BAC
=180°-
30°-30°=120°,
∵∠DAB=45°,
∴∠DAC=∠BAC-∠DAB=120°-45°=75°
(2)
∵∠DAB=45°,
∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,
∴DC=AC,
∴DC=AB.
23.(1)由BE平分∠ABC,DE//BC证得△BDE是等腰三角形;
(2)△ADE为等边三角形,得到AD=DE=3.
24.(1)连接DE,∵CD是AB边上的高,∴∠ADC=∠BDC=90°,
∵BE是AC边上的中线,∴AE=CE,∴DE=CE,∵BD=CE,∴BD=DE,∴点D在BE的垂直平分线上
25.(1)35°
(2)EF=BE-CF
26.∵△AEB是等腰直角三角形∵∠C=∠D=∠AEB=90°,AE=BE∴∠BEC+∠AED=∠AED+∠EAD=90°,∴∠BEC=∠EAD,∴Rt△AED≌Rt△EBC(AAS).
【探究】证明:∵Rt△AED≌Rt△EBC(AAS),∴BC=GM,又∵∠C=∠GMH=90°,∠CHB=∠MHG,∴△BCH≌△GMH(AAS),∴BH=GH,
【拓展】证明:如图2,在EG上取点M,使∠BME=∠AFE,
过点C作CN∥BM,交EG的延长线于点N,则∠N=∠BMG,
∵∠EAF+∠AFE+∠AEF=∠AEF+∠AEB+∠BEM=180°,∠EFA=∠AEB,
∴∠EAF=∠BEM,∵AE=BE∴△AEF≌△EBM,∴EF=BM,
∵∠AEB+∠DEC=180°,∠EFA+∠DFE=180°,而∠EFA=∠AEB,∴∠CED=∠EFD,∵∠BMG+∠BME=180°,∴∠N=∠EFD,∵∠EFD+∠EDF+∠FED=∠FED+∠DEC+∠CEN=180°,∴∠EDF=∠CEN,∵DE=CE∴△DEF≌△ECN,∴EF=CN∴BM=CN,又∵∠N=∠BMG,∠BGM=∠CGN,
∴△BGM≌△CGN(AAS),∴BG=CG.
一、选择题
1.下列图案属于轴对称图案的是 ( )
2.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上的点E处,若∠A=22°,则∠BDC的度数为
(
)
A.44°
B.60°
C.67°
D.77°
3.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为
(
)
A.1
B.2
C.3
D.4
(第2题)
(第3题)
(第4题)
4.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为点A,B.下列结论不一定成立的是(
)
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
5.等腰三角形的两边长分别为3cm和7cm,则周长为( )
A.13cm
B.17cm
C.13cm或17cm
D.11cm或17cm
6.到三角形三边的距离都相等的点是三角形的( )
A.三条角平分线的交点
B.三条边的中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
7.下列满足条件的三角形中,不是直角三角形的是
A.三内角之比为1:2:3
B.三边长的平方之比为1:2:3
C.三边长之比为3:4:5
D.三内角之比为3:4:5
8.已知等腰三角形的一个外角等于100°,则它的顶角是( )
A.80°
B.20°
C.80°或20°
D.不能确定
填空题
9.如图,在正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有_______种.
(第9题)
(第12题)
(第13题)
(第14题)
10.等腰三角形的周长为16,若一边长为6,则另两边的长为_______.
11.在△ABC中,∠A=400
,当∠C=
时,△ABC为等腰三角形.
12.如图,△ABC是等边三角形,D,E,F分别是AB,BC,CA边上的一点.若AD=BE=CF,则△DEF的形状是_______.
13.如图,在△ABC中,AB=AC,CD平分∠ACB,∠A=36°,则∠BDC=_______.
14.如图,在△ABC中,AB=AC,DE垂直平分AB.若BE⊥AC,AF⊥BC,垂足分别为点E,F,则么∠EFC=_______.
15.如图,△ABC中,∠C=90°,AC=3,AB=5,点D是边BC上一点.若沿AD将△ACD翻折,点C刚好落在AB边上点E处,则BD=
.
16.若直角三角形的三边分别为x,8,10,则=
.
17.已知直角三角形两边a,b满足,则斜边c上中线的长为
.
18.如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC=AD.有如下四个结论:CDAC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.请写出正确结论的序号_______.(填序号)
(第18题)
三、解答题
19.(1)已知△DEF,用直尺和圆规作点P,使点P到△DEF三边距离相等
(不写作法,保留作图痕迹).
(2)在图示的网格中,作出△ABC关于MN对称的图形△A1B1C1;
说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
20.现有9个相同的小正三角形拼成的大正三角形,将其部分涂黑.如图(1),(2)所示.观察图(1),图(2)中涂黑部分构成的图案.它们具有如下特征:①都是轴对称图形;②涂黑部分都是三个小正三角形.
请在图(3),图(4)内分别设计一个新图案,使图案具有上述两个特征.
21.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
22.如图,在△ABC中,AB=AC,D为边BC上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)求证:DC=AB.
23.如图,在△ABC中,AB=AC,BE平分∠ABC,DE∥BC,交AC于点D.
(1)求证:BD=DE;
(2)若∠DEB=30°且DE=3,求AD的长度.
24.如图,在△ABC中,CD是AB边上的高,BE是AC边上的中线,
BD=CE.
(1)求证:点D在BE的垂直平分线上;
(2)若∠ABE
=25°,求∠BEC的度数.
25.如图,在△ABC中,∠A=70°,BP是∠ABC的平分线,CP是∠ACD的平分线.
(1)如图1,求∠P的度数;
(2)如图2,过点P作EF∥BC,分别与边AB,AC交于点E,F,判断线段BE,EF,CF之间的数_______.量关系,并说明理由.
26.【感知】
如图1,在四边形ABCD中,∠C=∠ADC=90°,点E在边CD,且满足△AEB是等腰直角三角形,∠AEB=90°.求证:△ADE≌△ECB.
【探究】
如图2,在四边形ABCD中,∠C=∠ADC=90°,点E在边CD,且满足△AEB是等腰直角三角形,∠AEB=90°,点F在边AD的延长线上,连接EF,以EF为直角边作等腰Rt△EFG,过点G作GT⊥CD,垂足为T,连接BG交CD于点H.
求证:BH=GH.
【拓展】
如图3,点E在四边形ABCD内,∠AEB+∠DEC=180°,且AE=BE,DE=CE,过点E作EF交AD于点F,使∠EFA=∠AEB,延长FE交BC于点G.试探究BG与BC之间的数量关系,并说明理由.
第二章《轴对称图形》单元复习一(基础卷)
参考答案
一、选择题
1.A
2.C
3.B
4.D
5.B
6.A
7.D
8.C
二、填空题
9.3
10.5,5或6,4
11
40或70或
100°
12.等边三角形
13.72°
14.45°15.2.5
16.
36或164
17.4或5
18.①③
三、解答题
19.
(1)分别作两条角平分线交于点P,作出△A1B1C1,
(2)将它先向右平移6格,再向下平移2格得到△A2B2C
20.解:如图
21.(1)15cm
(2)40°
22.(1)
∵AB=AC,
∴∠B=∠C=30°,
∵∠C
+∠BAC+∠B=180°,
∴∠BAC
=180°-
30°-30°=120°,
∵∠DAB=45°,
∴∠DAC=∠BAC-∠DAB=120°-45°=75°
(2)
∵∠DAB=45°,
∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,
∴DC=AC,
∴DC=AB.
23.(1)由BE平分∠ABC,DE//BC证得△BDE是等腰三角形;
(2)△ADE为等边三角形,得到AD=DE=3.
24.(1)连接DE,∵CD是AB边上的高,∴∠ADC=∠BDC=90°,
∵BE是AC边上的中线,∴AE=CE,∴DE=CE,∵BD=CE,∴BD=DE,∴点D在BE的垂直平分线上
25.(1)35°
(2)EF=BE-CF
26.∵△AEB是等腰直角三角形∵∠C=∠D=∠AEB=90°,AE=BE∴∠BEC+∠AED=∠AED+∠EAD=90°,∴∠BEC=∠EAD,∴Rt△AED≌Rt△EBC(AAS).
【探究】证明:∵Rt△AED≌Rt△EBC(AAS),∴BC=GM,又∵∠C=∠GMH=90°,∠CHB=∠MHG,∴△BCH≌△GMH(AAS),∴BH=GH,
【拓展】证明:如图2,在EG上取点M,使∠BME=∠AFE,
过点C作CN∥BM,交EG的延长线于点N,则∠N=∠BMG,
∵∠EAF+∠AFE+∠AEF=∠AEF+∠AEB+∠BEM=180°,∠EFA=∠AEB,
∴∠EAF=∠BEM,∵AE=BE∴△AEF≌△EBM,∴EF=BM,
∵∠AEB+∠DEC=180°,∠EFA+∠DFE=180°,而∠EFA=∠AEB,∴∠CED=∠EFD,∵∠BMG+∠BME=180°,∴∠N=∠EFD,∵∠EFD+∠EDF+∠FED=∠FED+∠DEC+∠CEN=180°,∴∠EDF=∠CEN,∵DE=CE∴△DEF≌△ECN,∴EF=CN∴BM=CN,又∵∠N=∠BMG,∠BGM=∠CGN,
∴△BGM≌△CGN(AAS),∴BG=CG.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
