沪教版(上海)初中数学九年级第一学期 24.5 相似三角形复习 教案
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 24.5 相似三角形复习 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 58.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 23:40:34 | ||
图片预览

文档简介
课题:相似三角形复习教案(二)
一、教学目标
1、进一步巩固与掌握相似三角形的判定与性质定理。
2、熟练运用相似三角形的判定和性质解决有关问题,并在探究过程中运用一题多解、运动转化、图形化归等数学思想方法。
3、通过例题的分析、研究,揭示基本图形的变化,提高分析问题和解决问题的能力,养成在自主探究的过程中,仔细观察、大胆猜想、严格推理、合作解决问题的精神。
二、重点与难点
1、重点:利用相似三角形的判定与性质解决有关问题。
2、难点:灵活运用相似形的判定与性质,探究运动变化过程中图形的基本特征
。
三、教学技术与学习资源:多媒体辅助教学(几何画板)
四、教学过程
(一)基本图形回顾:
[问题设置]
如图△ABC中,已知点D、E分别在△ABC的边AB、AC上(点D不与点A、B重合,点E不与点A、C重合)
问题1、请添上一个条件,使得以点A、D、E为顶点的三角形与△ABC相似。(学生口答)
总结归纳并画出示意图:添加以下任意一个条件,都可以使得以点A、D、E为顶点与△ABC相似
①DE//BC
②∠ADE=∠B
③∠AED=∠C
④∠B+∠BDE=180°
⑤∠DEC+∠C=180°
⑥
⑥
⑦
⑧∠ADE=∠C
⑨∠AED=∠B
⑩
。
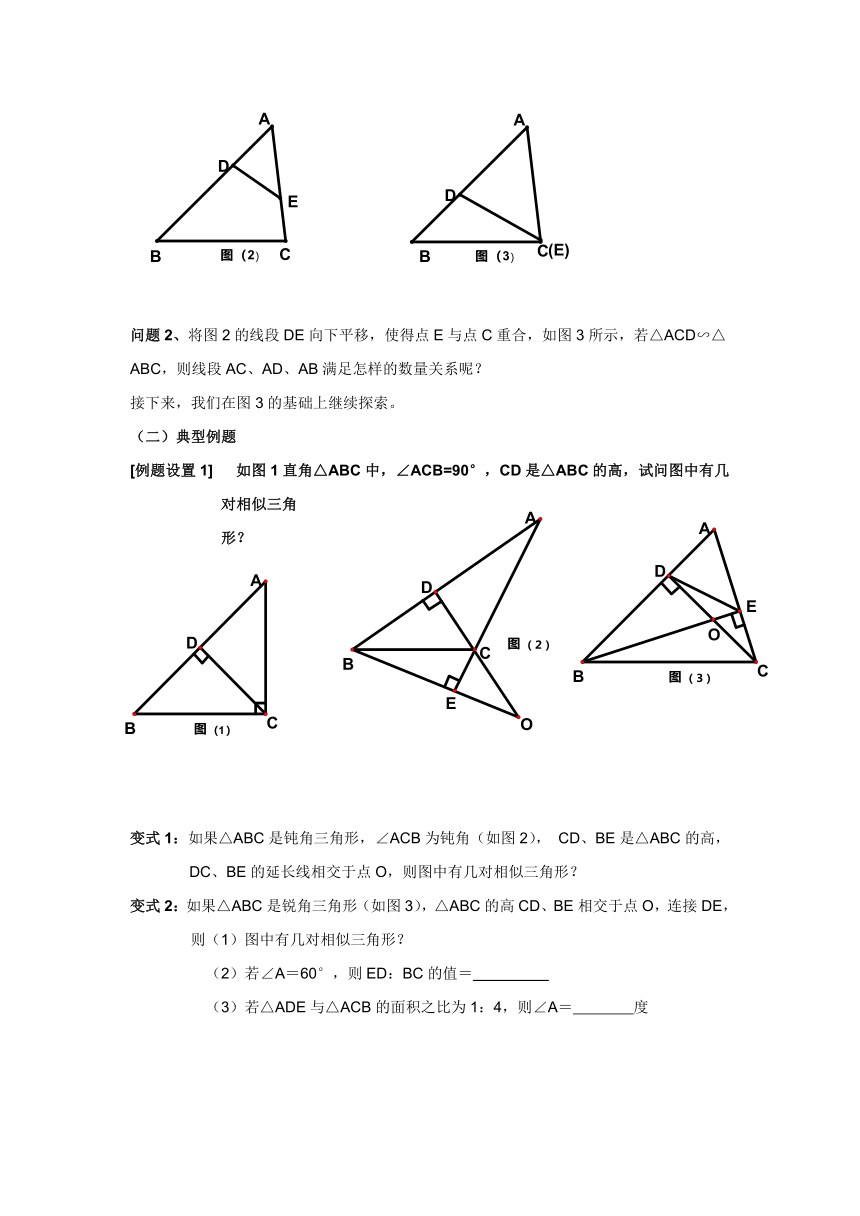
问题2、将图2的线段DE向下平移,使得点E与点C重合,如图3所示,若△ACD∽△ABC,则线段AC、AD、AB满足怎样的数量关系呢?
接下来,我们在图3的基础上继续探索。
(二)典型例题
[例题设置1]
如图1直角△ABC中,∠ACB=90°,CD是△ABC的高,试问图中有几对相似三角形?
变式1:如果△ABC是钝角三角形,∠ACB为钝角(如图2),
CD、BE是△ABC的高,DC、BE的延长线相交于点O,则图中有几对相似三角形?
变式2:如果△ABC是锐角三角形(如图3),△ABC的高CD、BE相交于点O,连接DE,则(1)图中有几对相似三角形?
(2)若∠A=60°,则ED:BC的值=
(3)若△ADE与△ACB的面积之比为1:4,则∠A= 度
[例题设置2]
如图四边形ABCD中,点E、F分别是线段AB、AC上两点,且AD//EF//BC
若AD=10,BC=16,,求线段EF的长。
(学生分小组探究本题多种解法,并作简要口述)
变式1:如图四边形ABCD中,点E、F分别是线段AB、AC上两点,且AD//EF//BC,连接BD、CA相交与点O,且点O正好在EF上(如图1),观察图1中有相等的线段吗?线段BC、AD、EO、OF有什么数量关系吗?
变式2:将图1中的线段EF向下平移,(如图2):在AD//EF//BC的条件下,你还能找到相等的线段吗?此时还有线段符合类似上述的数量关系吗?
变式3:(如图3)AD//OF//BC,AD=2,BC=3,则OF=
。
变式4:若图(3)增加条件∠DBC=90°,并以BD为边作正方形BDAH得图(4),猜测OB、OF的数量关系并证明。
三、课堂小结:通过这节课的复习,你学到了什么?你还有什么问题吗?
四、布置作业:①完成例1的变式2 ②例2 ③例2的变式3、4。
一、教学目标
1、进一步巩固与掌握相似三角形的判定与性质定理。
2、熟练运用相似三角形的判定和性质解决有关问题,并在探究过程中运用一题多解、运动转化、图形化归等数学思想方法。
3、通过例题的分析、研究,揭示基本图形的变化,提高分析问题和解决问题的能力,养成在自主探究的过程中,仔细观察、大胆猜想、严格推理、合作解决问题的精神。
二、重点与难点
1、重点:利用相似三角形的判定与性质解决有关问题。
2、难点:灵活运用相似形的判定与性质,探究运动变化过程中图形的基本特征
。
三、教学技术与学习资源:多媒体辅助教学(几何画板)
四、教学过程
(一)基本图形回顾:
[问题设置]
如图△ABC中,已知点D、E分别在△ABC的边AB、AC上(点D不与点A、B重合,点E不与点A、C重合)
问题1、请添上一个条件,使得以点A、D、E为顶点的三角形与△ABC相似。(学生口答)
总结归纳并画出示意图:添加以下任意一个条件,都可以使得以点A、D、E为顶点与△ABC相似
①DE//BC
②∠ADE=∠B
③∠AED=∠C
④∠B+∠BDE=180°
⑤∠DEC+∠C=180°
⑥
⑥
⑦
⑧∠ADE=∠C
⑨∠AED=∠B
⑩
。
问题2、将图2的线段DE向下平移,使得点E与点C重合,如图3所示,若△ACD∽△ABC,则线段AC、AD、AB满足怎样的数量关系呢?
接下来,我们在图3的基础上继续探索。
(二)典型例题
[例题设置1]
如图1直角△ABC中,∠ACB=90°,CD是△ABC的高,试问图中有几对相似三角形?
变式1:如果△ABC是钝角三角形,∠ACB为钝角(如图2),
CD、BE是△ABC的高,DC、BE的延长线相交于点O,则图中有几对相似三角形?
变式2:如果△ABC是锐角三角形(如图3),△ABC的高CD、BE相交于点O,连接DE,则(1)图中有几对相似三角形?
(2)若∠A=60°,则ED:BC的值=
(3)若△ADE与△ACB的面积之比为1:4,则∠A= 度
[例题设置2]
如图四边形ABCD中,点E、F分别是线段AB、AC上两点,且AD//EF//BC
若AD=10,BC=16,,求线段EF的长。
(学生分小组探究本题多种解法,并作简要口述)
变式1:如图四边形ABCD中,点E、F分别是线段AB、AC上两点,且AD//EF//BC,连接BD、CA相交与点O,且点O正好在EF上(如图1),观察图1中有相等的线段吗?线段BC、AD、EO、OF有什么数量关系吗?
变式2:将图1中的线段EF向下平移,(如图2):在AD//EF//BC的条件下,你还能找到相等的线段吗?此时还有线段符合类似上述的数量关系吗?
变式3:(如图3)AD//OF//BC,AD=2,BC=3,则OF=
。
变式4:若图(3)增加条件∠DBC=90°,并以BD为边作正方形BDAH得图(4),猜测OB、OF的数量关系并证明。
三、课堂小结:通过这节课的复习,你学到了什么?你还有什么问题吗?
四、布置作业:①完成例1的变式2 ②例2 ③例2的变式3、4。
