沪教版(上海)初中数学九年级第一学期第二十四章 相似三角形 本章小结 专题复习一类旋转相似三角形 教案
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期第二十四章 相似三角形 本章小结 专题复习一类旋转相似三角形 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 235.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:00:00 | ||
图片预览

文档简介
专题复习-
-
-
一类旋转相似三角形
教学目标
1、理解两个相似三角形绕一个顶点旋转得到的相关结论;
2、通过对基本图形的反思与总结,学会在复杂的图形中识别基本图形、构造基本图形,体会化归的思想方法,提高分析问题和解决问题的能力;
3、在解题过程中,培养学生的探究意识、反思意识,进一步提升思维品质.
教学重点
一类旋转相似三角形的识别与构造
教学难点
在具体问题情境中灵活运用基本图形
教学过程
一、总结基本图形:
引例(上海市九年级第一学期教材第32页)已知:如图,.
求证:△ADB∽AEC.
二、识别基本图形
1、如图,直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角(),得到Rt△,在三角板旋转的过程中,边与AB所在直线交于点D,过点D作DE∥交边于点E,联结BE,则
(1)BE:AD的值为
;
(2)设.设△EBD的面积为,则与之间的函数解析式为
.
2、如图,已知在△
ABC中AB
=
AC,点D为BC边的中点,点F在AB上,点E在线段DF的延长线上,且∠
BAE
=∠
BDF,点M在线段DF上,且∠
EBM
=∠
C.
(1)求证:;
(2)求证:AE⊥BE.
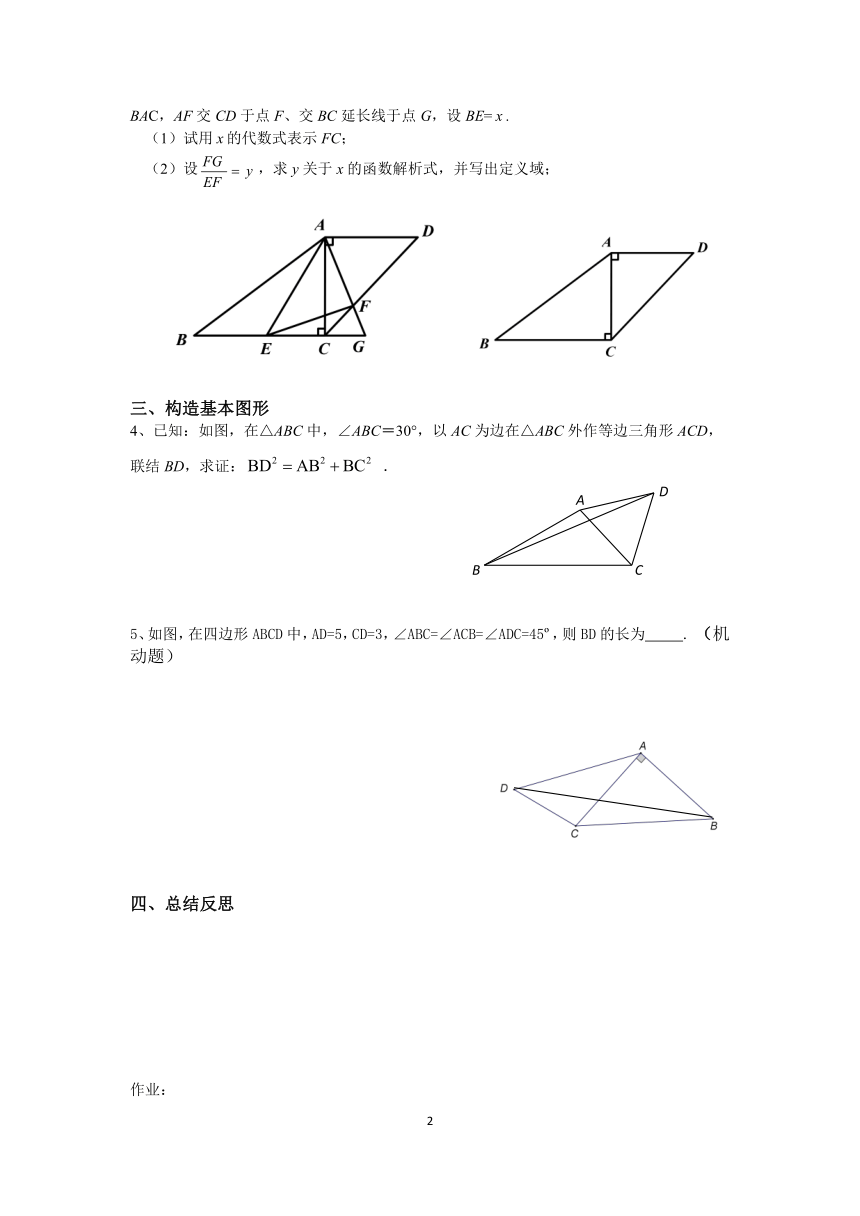
3、如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,
AD=9,AC=12,BC=16,点E是边BC上一个动点,∠EAF=∠BAC,AF交CD于点F、交BC延长线于点G,设BE=.
(1)试用的代数式表示FC;
(2)设,求y关于x的函数解析式,并写出定义域;
三、构造基本图形
4、已知:如图,在△ABC中,∠ABC=30°,以AC为边在△ABC外作等边三角形ACD,联结BD,求证:
.
5、如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45?,则BD的长为
.
(机动题)
四、总结反思
作业:
1、如图,在中,,,,将绕着点旋转得,点的对应点落在边上,联结,那么的长是_
.
2、如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A?B?C,点A的对应点A?落在中线AD上,且点A?是△ABC的重心,A?B?与BC相交于点E。则BE:EC=
.
3、如图,将□ABCD绕点A旋转到□AEFG的位置,其中点B、C、D分别落在点E、F、G处,且B、E、D、F在一条直线上,如果点E恰好是对角线BD的中点,则的值是 .
4、如图,已知等腰,是底边上的高,,将绕着点旋转,得,点分别与点对应,且与直线重合,
设与相交于点,则。
5、已知:如图,在△ABC中,∠ABC=45°,AB=
,BC=12,将线段AC绕点A逆时针旋转90°,得线段AD,联结BD,则BD的长为____________.
6、在等边△ABC和等边△DEF中,点O既是BC的中点,又是DE的中点,则AF:CE的值为
.
7、已知△ABC中,∠ABC=45°,AB=7
,BC=17,以AC为斜边在△ABC外作等腰直角三角形ACD,联结BD,则BD的长为____________.
8、已知:如图,在等腰直角△ABC中,
AC
=
BC,斜边AB的长为4,过点C作射线CP//AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.
(1)求证:△ADE∽△ACB;
(2)设CD=x,BAE
=
y,求y关于x的函数
解析式,并写出它的定义域;
(3)如果△COD与△BEA相似,求CD的值.
1
-
-
一类旋转相似三角形
教学目标
1、理解两个相似三角形绕一个顶点旋转得到的相关结论;
2、通过对基本图形的反思与总结,学会在复杂的图形中识别基本图形、构造基本图形,体会化归的思想方法,提高分析问题和解决问题的能力;
3、在解题过程中,培养学生的探究意识、反思意识,进一步提升思维品质.
教学重点
一类旋转相似三角形的识别与构造
教学难点
在具体问题情境中灵活运用基本图形
教学过程
一、总结基本图形:
引例(上海市九年级第一学期教材第32页)已知:如图,.
求证:△ADB∽AEC.
二、识别基本图形
1、如图,直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角(),得到Rt△,在三角板旋转的过程中,边与AB所在直线交于点D,过点D作DE∥交边于点E,联结BE,则
(1)BE:AD的值为
;
(2)设.设△EBD的面积为,则与之间的函数解析式为
.
2、如图,已知在△
ABC中AB
=
AC,点D为BC边的中点,点F在AB上,点E在线段DF的延长线上,且∠
BAE
=∠
BDF,点M在线段DF上,且∠
EBM
=∠
C.
(1)求证:;
(2)求证:AE⊥BE.
3、如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,
AD=9,AC=12,BC=16,点E是边BC上一个动点,∠EAF=∠BAC,AF交CD于点F、交BC延长线于点G,设BE=.
(1)试用的代数式表示FC;
(2)设,求y关于x的函数解析式,并写出定义域;
三、构造基本图形
4、已知:如图,在△ABC中,∠ABC=30°,以AC为边在△ABC外作等边三角形ACD,联结BD,求证:
.
5、如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45?,则BD的长为
.
(机动题)
四、总结反思
作业:
1、如图,在中,,,,将绕着点旋转得,点的对应点落在边上,联结,那么的长是_
.
2、如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A?B?C,点A的对应点A?落在中线AD上,且点A?是△ABC的重心,A?B?与BC相交于点E。则BE:EC=
.
3、如图,将□ABCD绕点A旋转到□AEFG的位置,其中点B、C、D分别落在点E、F、G处,且B、E、D、F在一条直线上,如果点E恰好是对角线BD的中点,则的值是 .
4、如图,已知等腰,是底边上的高,,将绕着点旋转,得,点分别与点对应,且与直线重合,
设与相交于点,则。
5、已知:如图,在△ABC中,∠ABC=45°,AB=
,BC=12,将线段AC绕点A逆时针旋转90°,得线段AD,联结BD,则BD的长为____________.
6、在等边△ABC和等边△DEF中,点O既是BC的中点,又是DE的中点,则AF:CE的值为
.
7、已知△ABC中,∠ABC=45°,AB=7
,BC=17,以AC为斜边在△ABC外作等腰直角三角形ACD,联结BD,则BD的长为____________.
8、已知:如图,在等腰直角△ABC中,
AC
=
BC,斜边AB的长为4,过点C作射线CP//AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.
(1)求证:△ADE∽△ACB;
(2)设CD=x,BAE
=
y,求y关于x的函数
解析式,并写出它的定义域;
(3)如果△COD与△BEA相似,求CD的值.
1
