沪科版八年级数学上册14.2:全等三角形判定培优讲义
文档属性
| 名称 | 沪科版八年级数学上册14.2:全等三角形判定培优讲义 |
|
|
| 格式 | zip | ||
| 文件大小 | 236.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-30 00:00:00 | ||
图片预览

文档简介
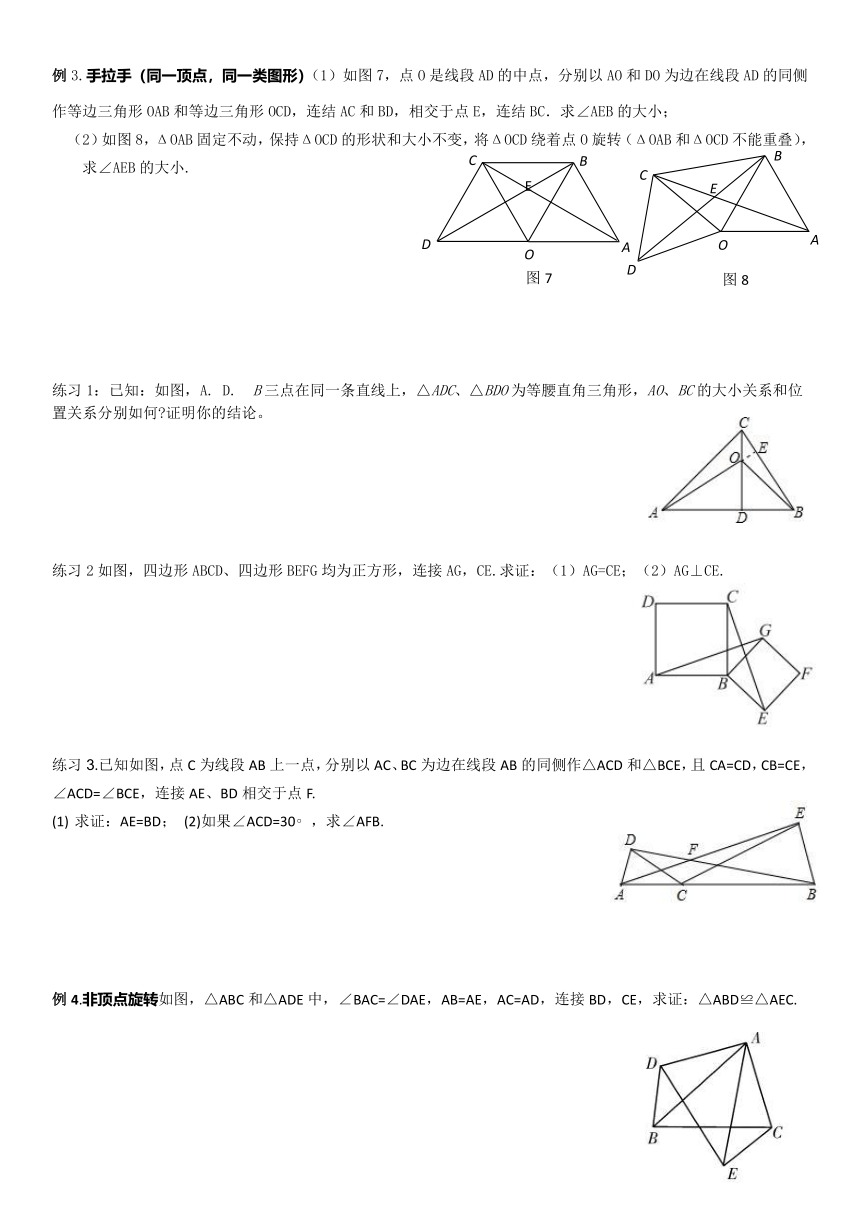
三角形全等判定培优训练1——图形变换
例1.翻折变换如图①,△ABC≌△DEF,将△ABC和△DEF的顶点B和顶点E重合,把△DEF绕点B顺时针方向旋转,这时AC与DF相交于点O.
⑴当△DEF旋转至如图②位置,点B(E)、C、D在同一直线上时,∠AFD与∠DCA的数量关系是________________;
⑵当△DEF继续旋转至如图③位置时,⑴中的结论成立吗?请说明理由_____________.
练习1:如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
练习2:如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB.求证:BD=CE.
练习3:如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.
例2.旋转变换.同一点旋转如图1所示,AB=AD,AC=AE,∠1=∠2.
(1)求证:BC=DE.
(2)如图2,若M、N分别为BC、DE的中点,试确定AM与AN的关系,并说明理由。
练习1.如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.
例3.手拉手(同一顶点,同一类图形)(1)如图7,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;
(2)如图8,ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),求∠AEB的大小.
练习1:已知:如图,A.
D.?B三点在同一条直线上,△ADC、△BDO为等腰直角三角形,AO、BC的大小关系和位置关系分别如何?证明你的结论。
练习2如图,四边形ABCD、四边形BEFG均为正方形,连接AG,CE.求证:(1)AG=CE;(2)AG⊥CE.
练习3.已知如图,点C为线段AB上一点,分别以AC、BC为边在线段AB的同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,连接AE、BD相交于点F.
求证:AE=BD;
(2)如果∠ACD=30?,求∠AFB.
例4.非顶点旋转如图,△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
练习1.已知BE,CF是△ABC的高,且BP=AC,CQ=AB,试确定AP与AQ的数量关系和位置关系
练习2.如图,在△ABC中,∠BAC=∠B=60?,AB=AC,点D.?E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.(1)当点D.?E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数,若变化,写出其变化规律;(2)当点D.?E运动到BC、AB的延长线上时,(1)中的结论是否改变?说明理由。
例5利用全等探索线段的数量关系.如图①所示,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B,C两点在AE的同侧,BD⊥AE于点D,CE⊥AE于点E.(1)求证:DE=BD+CE;
(2)若直线AE绕A旋转到如图②位置时(BO≥CO),其余条件不变,则DE与BD,CE的关系如何?请予以证明;
(3)若直线AE绕点A旋转如图③位置时(B0<C0),其余条件不变,则DE与BD,CE的关系如何?请直接写出结果,不需证明;(4)归纳(1)(2)(3),请用简洁的语言表达DE,BD,CE的关系.
.
例6.一线三等角已知,如图①,在△ABC中,∠BAC=90?,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.?E,求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D.
A.?E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由。
练习1.如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF交AB于点E,连接EG、EF.
(1)求证:BG=CF;
(2)求证:EG=EF;
(3)请你判断BE+CF与EF的大小关系,并证明你的结论。
练习2:如图,已知AD∥BC一点E为CD上一点,AE、BE分别平分∠DAB、∠CBA,BE交AD的延长线于点F.
(1)求证:△ABE≌△AFE;?(2)求证:AD+BC=AB.
练习3.已知,如图所示,在△ABC中,∠ABC=45?,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.?H是BC边上的中点,连接DH与BE相交于点G.(1)求证:BF=AC;(2)求证:CE=1/2BF;
练习4:如图,在△ABC中,已知AB=AC,点D.
E.?F分别在边BC、CA、AB上,且BD=CE,∠BDF=∠CED,那么∠FDE与∠B相等吗?为什么?
练习5.
直线CD经过的顶点C,CA=CB.E、F分别是直线CD上两点,且.
(1)若直线CD经过的内部,且E、F在射线CD上,请解决下面两个问题:
①如图1,若,则
(填“”,“”或“”号);
②如图2,若,若使①中的结论仍然成立,则
与
应满足的关系是
;
(2)如图3,若直线CD经过的外部,,请探究EF、与BE、AF三条线段的数量关系,并给予证明.
例1.翻折变换如图①,△ABC≌△DEF,将△ABC和△DEF的顶点B和顶点E重合,把△DEF绕点B顺时针方向旋转,这时AC与DF相交于点O.
⑴当△DEF旋转至如图②位置,点B(E)、C、D在同一直线上时,∠AFD与∠DCA的数量关系是________________;
⑵当△DEF继续旋转至如图③位置时,⑴中的结论成立吗?请说明理由_____________.
练习1:如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.
练习2:如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB.求证:BD=CE.
练习3:如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.
例2.旋转变换.同一点旋转如图1所示,AB=AD,AC=AE,∠1=∠2.
(1)求证:BC=DE.
(2)如图2,若M、N分别为BC、DE的中点,试确定AM与AN的关系,并说明理由。
练习1.如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.
例3.手拉手(同一顶点,同一类图形)(1)如图7,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;
(2)如图8,ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),求∠AEB的大小.
练习1:已知:如图,A.
D.?B三点在同一条直线上,△ADC、△BDO为等腰直角三角形,AO、BC的大小关系和位置关系分别如何?证明你的结论。
练习2如图,四边形ABCD、四边形BEFG均为正方形,连接AG,CE.求证:(1)AG=CE;(2)AG⊥CE.
练习3.已知如图,点C为线段AB上一点,分别以AC、BC为边在线段AB的同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,连接AE、BD相交于点F.
求证:AE=BD;
(2)如果∠ACD=30?,求∠AFB.
例4.非顶点旋转如图,△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
练习1.已知BE,CF是△ABC的高,且BP=AC,CQ=AB,试确定AP与AQ的数量关系和位置关系
练习2.如图,在△ABC中,∠BAC=∠B=60?,AB=AC,点D.?E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.(1)当点D.?E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数,若变化,写出其变化规律;(2)当点D.?E运动到BC、AB的延长线上时,(1)中的结论是否改变?说明理由。
例5利用全等探索线段的数量关系.如图①所示,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B,C两点在AE的同侧,BD⊥AE于点D,CE⊥AE于点E.(1)求证:DE=BD+CE;
(2)若直线AE绕A旋转到如图②位置时(BO≥CO),其余条件不变,则DE与BD,CE的关系如何?请予以证明;
(3)若直线AE绕点A旋转如图③位置时(B0<C0),其余条件不变,则DE与BD,CE的关系如何?请直接写出结果,不需证明;(4)归纳(1)(2)(3),请用简洁的语言表达DE,BD,CE的关系.
.
例6.一线三等角已知,如图①,在△ABC中,∠BAC=90?,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.?E,求证:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D.
A.?E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明:若不成立,请说明理由。
练习1.如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF交AB于点E,连接EG、EF.
(1)求证:BG=CF;
(2)求证:EG=EF;
(3)请你判断BE+CF与EF的大小关系,并证明你的结论。
练习2:如图,已知AD∥BC一点E为CD上一点,AE、BE分别平分∠DAB、∠CBA,BE交AD的延长线于点F.
(1)求证:△ABE≌△AFE;?(2)求证:AD+BC=AB.
练习3.已知,如图所示,在△ABC中,∠ABC=45?,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.?H是BC边上的中点,连接DH与BE相交于点G.(1)求证:BF=AC;(2)求证:CE=1/2BF;
练习4:如图,在△ABC中,已知AB=AC,点D.
E.?F分别在边BC、CA、AB上,且BD=CE,∠BDF=∠CED,那么∠FDE与∠B相等吗?为什么?
练习5.
直线CD经过的顶点C,CA=CB.E、F分别是直线CD上两点,且.
(1)若直线CD经过的内部,且E、F在射线CD上,请解决下面两个问题:
①如图1,若,则
(填“”,“”或“”号);
②如图2,若,若使①中的结论仍然成立,则
与
应满足的关系是
;
(2)如图3,若直线CD经过的外部,,请探究EF、与BE、AF三条线段的数量关系,并给予证明.
