沪教版(上海)数学八年级第二学期-22.4 四 边 形 复 习(二)—梯形 课件
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.4 四 边 形 复 习(二)—梯形 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 364.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 19:16:49 | ||
图片预览




文档简介
(共26张PPT)
四
边
形
复
习(二)
——梯形
中考第一轮专题复习六
第三单元
1、概念辨析
1)四边形可以分为平行四边形和梯形两类
(
)
2)直角梯形和等腰梯形是两种特殊的梯形
(
)
3)梯形的对角线相等
(
)
X
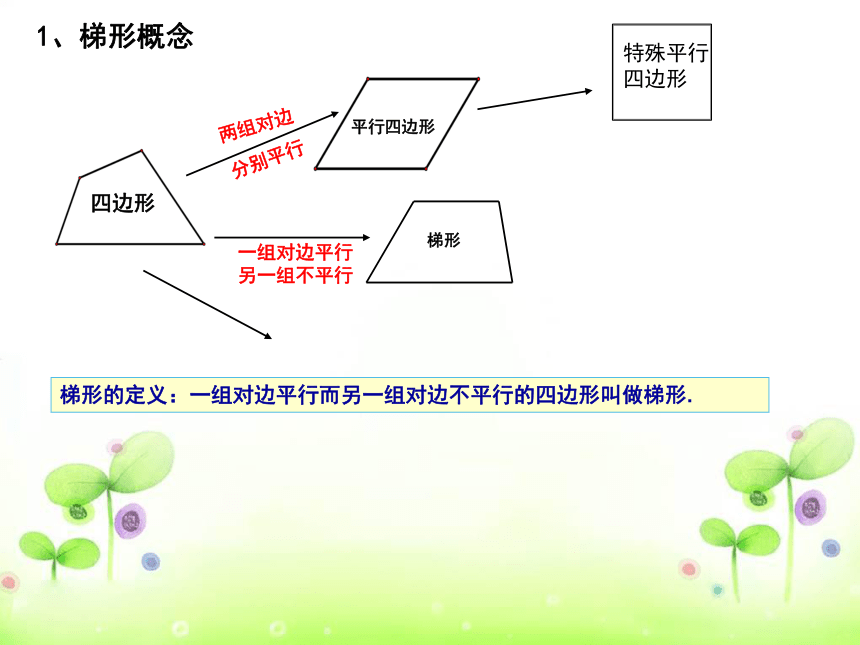
1、梯形概念
四边形
平行四边形
两组对边
分别平行
一组对边平行
另一组不平行
梯形
梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.
特殊平行四边形
1、概念辨析
1)四边形可以分为平行四边形和梯形两类
(
X
)
2)等腰梯形和直角梯形是两种特殊的梯形
(
)
3)梯形的对角线相等
(
)
√
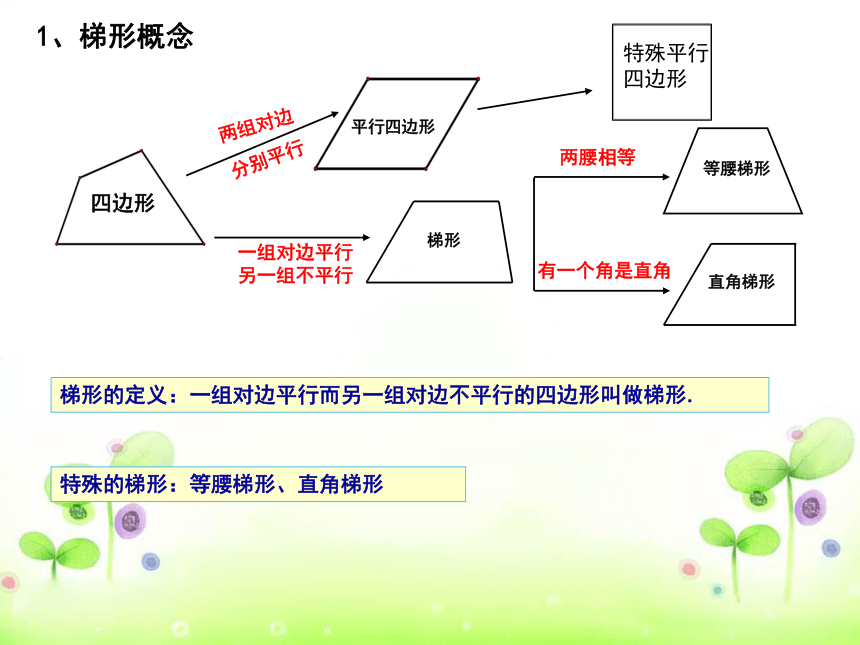
1、梯形概念
四边形
平行四边形
两组对边
分别平行
一组对边平行
另一组不平行
直角梯形
两腰相等
等腰梯形
梯形
有一个角是直角
梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.
特殊的梯形:等腰梯形、直角梯形
特殊平行四边形
1、概念辨析
1)四边形可以分为平行四边形和梯形两类
(
X
)
2)等腰梯形和直角梯形是两种特殊的梯形
(
√
)
3)梯形的对角线相等
(
)
X
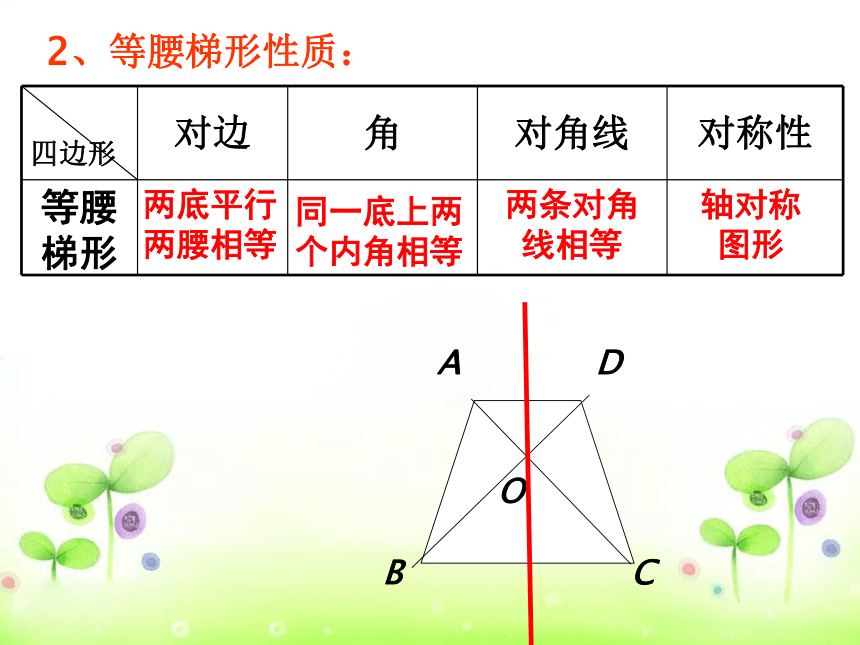
四边形
对边
角
对角线
对称性
同一底上两个内角相等
两条对角线相等
轴对称图形
2、等腰梯形性质:
等腰梯形
两底平行两腰相等
A
B
C
D
O
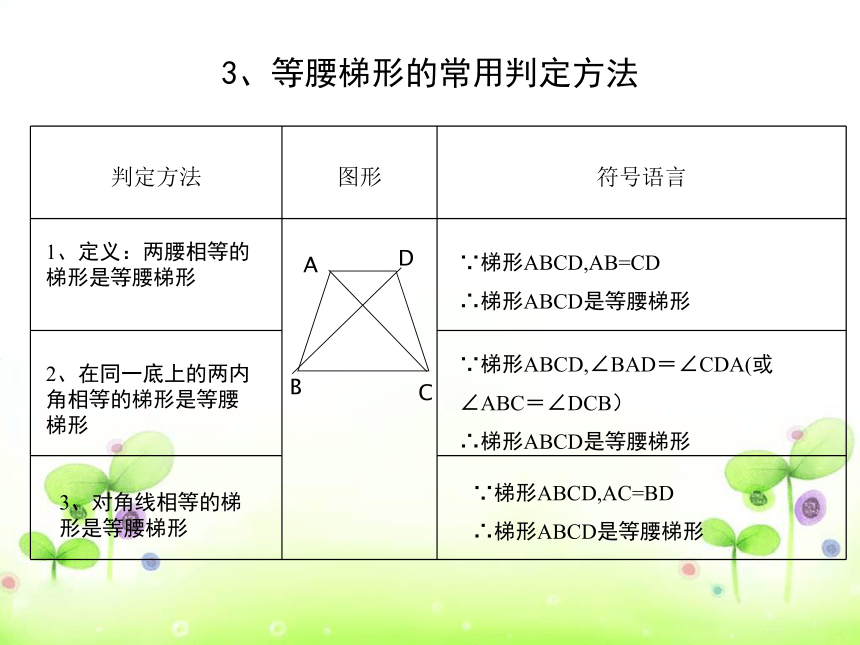
判定方法
图形
符号语言
3、等腰梯形的常用判定方法
1、定义:两腰相等的梯形是等腰梯形
∵梯形ABCD,AB=CD
∴梯形ABCD是等腰梯形
2、在同一底上的两内角相等的梯形是等腰梯形
∵梯形ABCD,∠BAD=∠CDA(或∠ABC=∠DCB)
∴梯形ABCD是等腰梯形
3、对角线相等的梯形是等腰梯形
∵梯形ABCD,AC=BD
∴梯形ABCD是等腰梯形
A
B
C
D
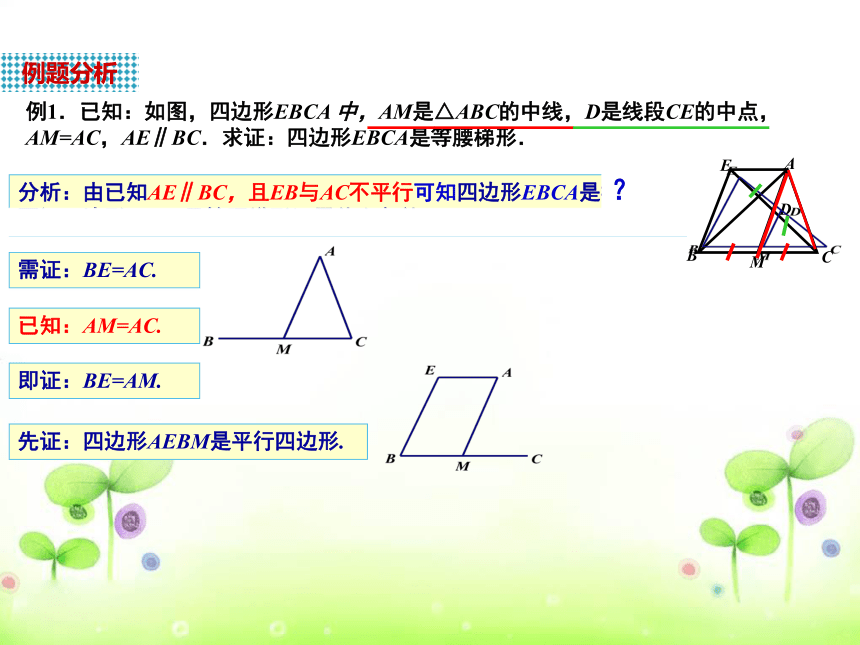
例1.已知:如图,四边形EBCA
中,AM是△ABC的中线,D是线段CE的中点,
AM=AC,AE∥BC.求证:四边形EBCA是等腰梯形.
分析:由已知AE∥BC,且EB与AC不平行可知四边形EBCA是梯形,要证四边形EBCA是等腰梯形还需什么条件?
例题分析
A
E
B
M
C
D
?
需证:BE=AC.
已知:AM=AC.
即证:BE=AM.
先证:四边形AEBM是平行四边形.
例1.已知:如图,AM是△ABC的中线,D是线段CE的中点,
AM=AC,AE∥BC.求证:四边形EBCA是等腰梯形.
例题分析
A
E
B
M
C
D
证明:
∵
AE∥BC且D是线段CE的中点,
∴
DM是△CEB的中位线.
∴AM∥EB.
∵
AE∥BC,
∵
AM是△ABC的中线
∴四边形EBMA是平行四边形.
∴AM=EB.
∴
EB=AC.
∴四边形EBCA是梯形.
∵
AM=AC,
∵
AE∥BC且
EB与AC不平行,
∴四边形EBCA是等腰梯形.
∵
EB=AC
【小结】要证明一个四边形是等腰梯形,先要证明它是一个梯形.
3、梯形的中位线
什么叫做梯形的中位线,它有什么的性质?
联结梯形两腰的中点的线段叫做梯形的中位线.
梯形的中位线平行于两底,并且等于两底和的一半.
梯形的中位线=
联结三角形两边的中点的线段叫做三角形的中位线.
三角形的中位线平行于第三边,并且等于第三边的一半.
4、梯形面积公式。
梯形的面积公式=
=
中位线×高
例3、(1)梯形ABCD中,AD∥BC,AB=CD=6,AD=4,∠B=60°,则下底BC的长是____________.
A
B
C
D
(请你用多种方法解决这个问题)
5、回顾常用辅助线添加
2、等腰梯形ABCD,AD//BC,AB=CD,对角线AC⊥BD于O,若AD=6,BC=8,求梯形的高是
.
O
(3)、如图,梯形ABCD中,AD=1,BC=4,AD∥BC,E是AB的中点,DE⊥CE,CD=_________
.
.
梯形中常用的辅助线:
延腰交于一点
作高
平移腰
平移对角线
连中位线
连一腰中点并延长
方法一,由点E是CD的中点及待证结论,
联想梯形中位线性质
方法二,由结论想到作一条长度等于AD+BC的线段,于是考虑把AD平移到与BC相接的位置;
分析:
例题分析
证明:(方法二)联结AE并延长交BC的延长线于点G
∵
E是CD的中点,可知,DE=EC
∵
AD//BC,
∴AD=CG,AE=EG
∴
BG=AD+BC
∵
BG=BC+CG,
例4.已知:如图,在梯形ABCD中,AD//BC,点E是边CD的中点,点F在边BC上
,EF//AB.
求证:
从而取AB中点M,
∴
,
∴
∵在
中,EF//AB
∴
∴BF=FG,即BF=
BG=
E
F
D
C
B
A
可通过联结AE并延长交BC的延长线于G来实现
这样就只要证明F是线段BG的中点即可.
只要证明ME=BF
G
E
F
D
C
B
A
1
2
M
方法二,由结论想到作一条长度等于AD+BC的线段,于是考虑把AD平移到与BC相接的位置;
分析:
例题分析
说明:解决有关梯形的问题时,常要通过添加辅助线构造三角形
或平行四边形将问题转化,本题还可如方法三所示添加辅助线,
构造全等三角形,进而证明结论.
方法三:考虑把FC平移到与AD相接的位置;
1
2
G
E
F
D
C
B
A
E
F
D
C
B
A
G
E
F
D
C
B
A
可通过联结AE并延长交BC的延长线于G来实现
这样就只要证明F是线段BG的中点即可.
可通过延长FE交AD的延长线于G来实现
这样就只要证明DG=FC即可.
方法一,由点E是CD的中点及待证结论,
联想梯形中位线性质
从而取AB中点M,
只要证明ME=BF
例4.(学科基本要求P109
例3)已知:如图,在梯形ABCD中,AD//BC,点E是边CD的中点,点F在边BC上
,EF//AB.
求证:
M
小结:
谈谈这节课你有什么收获、体会或想法?
?
?
布置作业:二模练习
M
H
M
H
2、过梯形ABCD一腰中点M向另一腰作垂线,垂足为H,
中考要求:
1、懂得梯形的有关概念
2、掌握等腰梯形的性质与判定
3、掌握梯形中位线定理
4、掌握梯形常用辅助线添加
四
边
形
复
习(二)
——梯形
中考第一轮专题复习六
第三单元
1、概念辨析
1)四边形可以分为平行四边形和梯形两类
(
)
2)直角梯形和等腰梯形是两种特殊的梯形
(
)
3)梯形的对角线相等
(
)
X
1、梯形概念
四边形
平行四边形
两组对边
分别平行
一组对边平行
另一组不平行
梯形
梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.
特殊平行四边形
1、概念辨析
1)四边形可以分为平行四边形和梯形两类
(
X
)
2)等腰梯形和直角梯形是两种特殊的梯形
(
)
3)梯形的对角线相等
(
)
√
1、梯形概念
四边形
平行四边形
两组对边
分别平行
一组对边平行
另一组不平行
直角梯形
两腰相等
等腰梯形
梯形
有一个角是直角
梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.
特殊的梯形:等腰梯形、直角梯形
特殊平行四边形
1、概念辨析
1)四边形可以分为平行四边形和梯形两类
(
X
)
2)等腰梯形和直角梯形是两种特殊的梯形
(
√
)
3)梯形的对角线相等
(
)
X
四边形
对边
角
对角线
对称性
同一底上两个内角相等
两条对角线相等
轴对称图形
2、等腰梯形性质:
等腰梯形
两底平行两腰相等
A
B
C
D
O
判定方法
图形
符号语言
3、等腰梯形的常用判定方法
1、定义:两腰相等的梯形是等腰梯形
∵梯形ABCD,AB=CD
∴梯形ABCD是等腰梯形
2、在同一底上的两内角相等的梯形是等腰梯形
∵梯形ABCD,∠BAD=∠CDA(或∠ABC=∠DCB)
∴梯形ABCD是等腰梯形
3、对角线相等的梯形是等腰梯形
∵梯形ABCD,AC=BD
∴梯形ABCD是等腰梯形
A
B
C
D
例1.已知:如图,四边形EBCA
中,AM是△ABC的中线,D是线段CE的中点,
AM=AC,AE∥BC.求证:四边形EBCA是等腰梯形.
分析:由已知AE∥BC,且EB与AC不平行可知四边形EBCA是梯形,要证四边形EBCA是等腰梯形还需什么条件?
例题分析
A
E
B
M
C
D
?
需证:BE=AC.
已知:AM=AC.
即证:BE=AM.
先证:四边形AEBM是平行四边形.
例1.已知:如图,AM是△ABC的中线,D是线段CE的中点,
AM=AC,AE∥BC.求证:四边形EBCA是等腰梯形.
例题分析
A
E
B
M
C
D
证明:
∵
AE∥BC且D是线段CE的中点,
∴
DM是△CEB的中位线.
∴AM∥EB.
∵
AE∥BC,
∵
AM是△ABC的中线
∴四边形EBMA是平行四边形.
∴AM=EB.
∴
EB=AC.
∴四边形EBCA是梯形.
∵
AM=AC,
∵
AE∥BC且
EB与AC不平行,
∴四边形EBCA是等腰梯形.
∵
EB=AC
【小结】要证明一个四边形是等腰梯形,先要证明它是一个梯形.
3、梯形的中位线
什么叫做梯形的中位线,它有什么的性质?
联结梯形两腰的中点的线段叫做梯形的中位线.
梯形的中位线平行于两底,并且等于两底和的一半.
梯形的中位线=
联结三角形两边的中点的线段叫做三角形的中位线.
三角形的中位线平行于第三边,并且等于第三边的一半.
4、梯形面积公式。
梯形的面积公式=
=
中位线×高
例3、(1)梯形ABCD中,AD∥BC,AB=CD=6,AD=4,∠B=60°,则下底BC的长是____________.
A
B
C
D
(请你用多种方法解决这个问题)
5、回顾常用辅助线添加
2、等腰梯形ABCD,AD//BC,AB=CD,对角线AC⊥BD于O,若AD=6,BC=8,求梯形的高是
.
O
(3)、如图,梯形ABCD中,AD=1,BC=4,AD∥BC,E是AB的中点,DE⊥CE,CD=_________
.
.
梯形中常用的辅助线:
延腰交于一点
作高
平移腰
平移对角线
连中位线
连一腰中点并延长
方法一,由点E是CD的中点及待证结论,
联想梯形中位线性质
方法二,由结论想到作一条长度等于AD+BC的线段,于是考虑把AD平移到与BC相接的位置;
分析:
例题分析
证明:(方法二)联结AE并延长交BC的延长线于点G
∵
E是CD的中点,可知,DE=EC
∵
AD//BC,
∴AD=CG,AE=EG
∴
BG=AD+BC
∵
BG=BC+CG,
例4.已知:如图,在梯形ABCD中,AD//BC,点E是边CD的中点,点F在边BC上
,EF//AB.
求证:
从而取AB中点M,
∴
,
∴
∵在
中,EF//AB
∴
∴BF=FG,即BF=
BG=
E
F
D
C
B
A
可通过联结AE并延长交BC的延长线于G来实现
这样就只要证明F是线段BG的中点即可.
只要证明ME=BF
G
E
F
D
C
B
A
1
2
M
方法二,由结论想到作一条长度等于AD+BC的线段,于是考虑把AD平移到与BC相接的位置;
分析:
例题分析
说明:解决有关梯形的问题时,常要通过添加辅助线构造三角形
或平行四边形将问题转化,本题还可如方法三所示添加辅助线,
构造全等三角形,进而证明结论.
方法三:考虑把FC平移到与AD相接的位置;
1
2
G
E
F
D
C
B
A
E
F
D
C
B
A
G
E
F
D
C
B
A
可通过联结AE并延长交BC的延长线于G来实现
这样就只要证明F是线段BG的中点即可.
可通过延长FE交AD的延长线于G来实现
这样就只要证明DG=FC即可.
方法一,由点E是CD的中点及待证结论,
联想梯形中位线性质
从而取AB中点M,
只要证明ME=BF
例4.(学科基本要求P109
例3)已知:如图,在梯形ABCD中,AD//BC,点E是边CD的中点,点F在边BC上
,EF//AB.
求证:
M
小结:
谈谈这节课你有什么收获、体会或想法?
?
?
布置作业:二模练习
M
H
M
H
2、过梯形ABCD一腰中点M向另一腰作垂线,垂足为H,
中考要求:
1、懂得梯形的有关概念
2、掌握等腰梯形的性质与判定
3、掌握梯形中位线定理
4、掌握梯形常用辅助线添加
