2020-2021学年江苏省南京师大附中高三上学期期中数学试卷 (Word版含解析)
文档属性
| 名称 | 2020-2021学年江苏省南京师大附中高三上学期期中数学试卷 (Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 19:58:55 | ||
图片预览




文档简介
2020-2021学年江苏省南京师大附中高三(上)期中数学试卷
一、选择题(共12小题).
1.(3分)已知集合M={x|(x﹣1)2<4,x∈R},N={﹣2,﹣1,0,1,2},则M∩N=( )
A.{0,1,2} B.{﹣1,0,1,2} C.{﹣1,0,2,3} D.{0,1,2,3}
2.(3分)设z=,则z的虚部为( )
A. B.﹣ C. D.﹣
3.(3分)已知m,n∈R,则“mn<0”是“抛物线mx2+ny=0的焦点在y轴正半轴上”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.(3分)设λ为实数,已知向量=(﹣1,2),=(1,λ).若⊥,则向量+2与之间的夹角为( )
A. B. C. D.
5.(3分)音乐与数学有着密切的联系,我国春秋时期有个著名的“三分损益法”:以“宫”为基本音,“宫”经过一次“损”,频率变为原来的,得到“徵”;“徵”经过一次“益”,频率变为原来的,得到“商”;…….依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶.据此可推得( )
A.“宫、商、角”的频率成等比数列
B.“宫、徵、商”的频率成等比数列
C.“商、羽、角”的频率成等比数列
D.“徵、商、羽”的频率成等比数列
6.(3分)若函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)图象的一条对称轴是( )
A.x= B.x=﹣ C.x= D.x=
7.(3分)函数f(x)=ex﹣x2﹣2x的图象大致为( )
A. B.
C. D.
8.(3分)设实数k,已知函数f(x)=,若函数f(x)﹣k在区间(0,+∞)上有两个零点x1,x2(x1<x2),则(x2﹣x1)f(x1)的取值范围是( )
A.[1,e2] B.[﹣1,e) C.[e,e2) D.[2,e2)
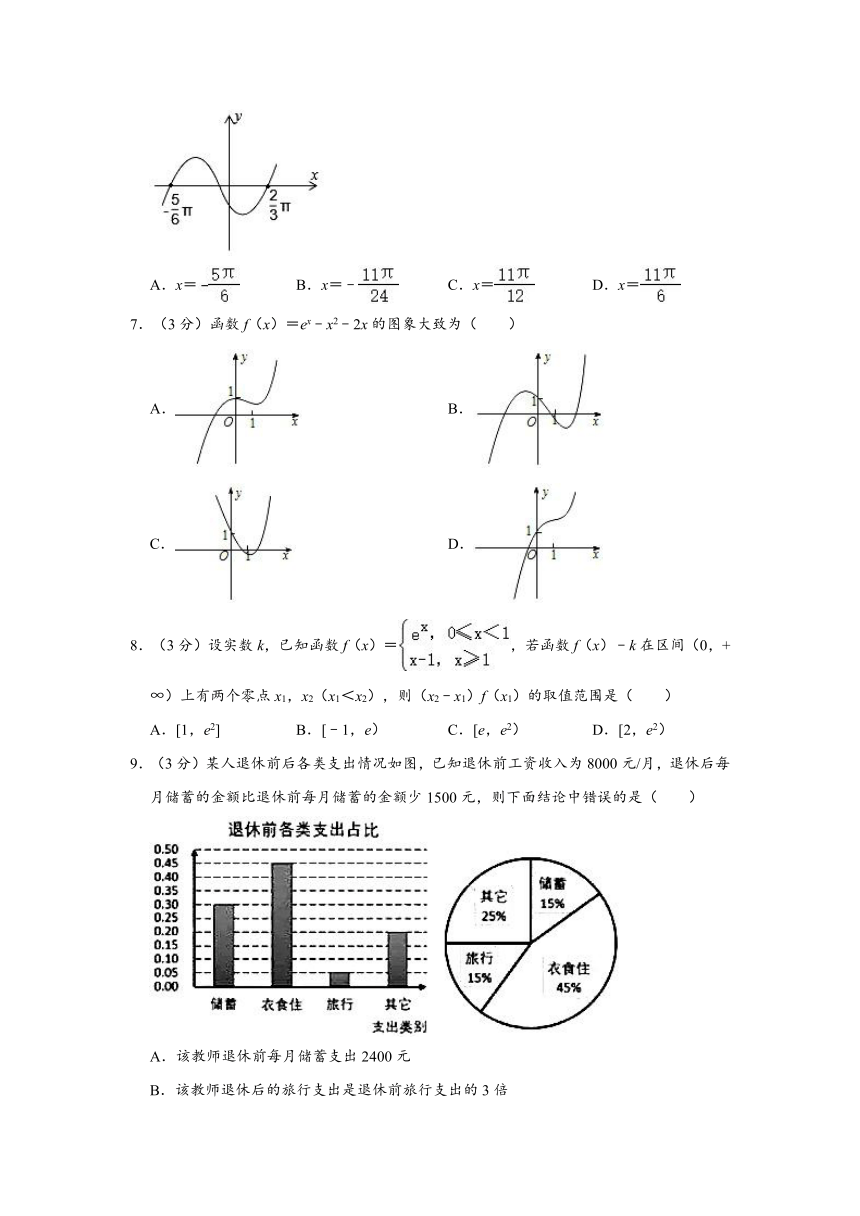
9.(3分)某人退休前后各类支出情况如图,已知退休前工资收入为8000元/月,退休后每月储蓄的金额比退休前每月储蓄的金额少1500元,则下面结论中错误的是( )
A.该教师退休前每月储蓄支出2400元
B.该教师退休后的旅行支出是退休前旅行支出的3倍
C.该教师退休工资收入为6000元/月
D.该教师退休后的其他支出比退休前的其他支出少
10.(3分)在平面直角坐标系xOy中,已知双曲线C:=1(a>0,b>0)的焦点在圆O:x2+y2=20上,圆O与双曲线C的渐近线在第一、二象限分别交于M、N两点,若点E(0,3)满足ME⊥ON(O为坐标原点),下列说法正确的有( )
A.双曲线C的虚轴长为4
B.双曲线的离心率为
C.双曲线C的一条渐近线方程为y=x
D.三角形OMN的面积为8
11.(3分)在正方体ABCD﹣A1B1C1D1中,AB=2,E、F分别为BB1、CD中点,P是BC1上的动点,则下列说法正确的有( )
A.A1F⊥AE
B.三棱锥P﹣AED1的体积与点P位置有关系
C.平面AED1截正方体ABCD﹣A1B1C1D的截面面积为
D.点A到平面AED1的距离为
12.(3分)已知函数f(x)=+cosx﹣(x∈R),则下列说法错误的有( )
A.直线y=0为曲线y=f(x)的一条切线
B.f(x)的极值点个数为3
C.f(x)的零点个数为4
D.若f(x1)=f(x2)(x1≠x2),则x1+x2=0
三、填空题(共4小题)
13.(3分)二项式(2x﹣)6的展开式中x3的系数为 .
14.(3分)已知α、β均为锐角,且sinα=,cos(α+β)=,则cos2β= .
15.(3分)设a,b为实数,对于任意的a≥2,关于x的不等式x≤eax+b(e为自然对数的底数)在实数域R上恒成立,则b的取值范围为 .
16.(3分)农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为 ;若该六面体内有一球,则该球表面积的最大值为 .
三、解答题
17.在△ABC中,设内角A,B,C所对的边分别为a,b,c,已知bcosC+ccosB=﹣4cosA,a=2.
(1)求角A的值;
(2)若三角形ABC的面积为,求△ABC的周长.
18.已知函数f(x)=ax(a为常数,a>0且a≠1)
(1)在下列条件中选择一个条件_____(仅填序号),使得以此条件可以推出数列{an}为等差数列,并说明理由;
①数列{f(an)}是首项为4,公比为2的等比数列;
②数列{f(an)}是首项为4,公差为2的等差数列;
③数列{f(an)}是首项为4,公比为2的等比数列的前n项和构成的数列;
(2)在(1)的选择下,若a=2,b=(n∈N*),求数列{an?bn}的前n项和Sn.
19.如图,在四棱台ABCD﹣A1B1C1D1中,底面ABCD是菱形,AA1=A1B1=AB=1,∠ABC=60°,AA1⊥平面ABCD,点E是棱BC上一点.
(1)若E是BC中点,求证:平面AD1E⊥平面CC1D1D;
(2)设二面角E﹣AD1﹣D的平面角为θ,且|cosθ|=,求线段CE的长.
20.第13届女排世界杯于2019年9月14日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球MIKSA﹣V200W,已知这种球的质量指标ξ(单位:g)服从正态分布N(270,52).比赛赛制采取单循环方式,即每支球队进行11场比赛(采取5局3胜制),最后靠积分选出最后冠军积分规则如下:比赛中以3:0或3:1取胜的球队积3分,负队积0分;而在比赛中以3:2取胜的球队积2分,负队积1分.已知第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为p(0<p<1).
(1)如果比赛准备了1000个排球,估计质量指标在(260,265]内的排球个数(计算结果取整数).
(2)第10轮比赛中,记中国队3:1取胜的概率为f(p).
(ⅰ)求出f(p)的最大值点p0;
(ⅱ)若以p0作为p的值记第10轮比赛中,中国队所得积分为X,求X的分布列.
参考数据:ξ~N(u,σ2),则p(μ﹣σ<X<μ+σ)≈0.6826,p(μ﹣2σ<X<μ+2σ)≈0.9644.
21.设a为实数,已知函数f(x)=ex+ae﹣x+(1﹣a)x﹣2.
(1)当a=2时,求f(x)的单调区间;
(2)当a≥1时,若f(x)有两个不同的零点,求a的取值范围.
22.在平面直角坐标系xOy中,已知椭圆C:=1(a>b>0)的离心率为,以椭圆上的一点和长轴的两个端点为顶点的三角形面积最大值为.
(1)求a,b的值;
(2)当过点P(6,0)的动直线l与椭圆C交于不同的点A,B时,在线段AB上取点Q,使得||?||=||?||,问:点Q是否总在某条定直线上?若是,求出该直线方程,若不是,说明理由.
参考答案
一、单项选择题
1.(3分)已知集合M={x|(x﹣1)2<4,x∈R},N={﹣2,﹣1,0,1,2},则M∩N=( )
A.{0,1,2} B.{﹣1,0,1,2} C.{﹣1,0,2,3} D.{0,1,2,3}
解:由M中不等式变形得:﹣2<x﹣1<2,
解得:﹣1<x<3,即M=(﹣1,3),
∵N={﹣2.﹣1,0,1,2},
∴M∩N={0,1,2}.
故选:A.
2.(3分)设z=,则z的虚部为( )
A. B.﹣ C. D.﹣
解:∵z====+i,
∴z的虚部为,
故选:A.
3.(3分)已知m,n∈R,则“mn<0”是“抛物线mx2+ny=0的焦点在y轴正半轴上”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解:抛物线mx2+ny=0的焦点在y轴正半轴上?>0,即mn<0,
∴“mn<0”是“抛物线mx2+ny=0的焦点在y轴正半轴上”的充要条件.
故选:C.
4.(3分)设λ为实数,已知向量=(﹣1,2),=(1,λ).若⊥,则向量+2与之间的夹角为( )
A. B. C. D.
解:λ为实数,已知向量=(﹣1,2),=(1,λ),
若⊥,则﹣1×1+2λ=0,解得λ=,
所以=(1,),+2=(1,3),
设+2与之间的夹角为θ,
则(+2)?=2+2?=5+0=5,
再根据(+2)?=|+2|?||?cosθ=??cosθ,
所以??cosθ=5,求得cosθ=,
由0≤θ≤π,
所以θ=,
故选:A.
5.(3分)音乐与数学有着密切的联系,我国春秋时期有个著名的“三分损益法”:以“宫”为基本音,“宫”经过一次“损”,频率变为原来的,得到“徵”;“徵”经过一次“益”,频率变为原来的,得到“商”;…….依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶.据此可推得( )
A.“宫、商、角”的频率成等比数列
B.“宫、徵、商”的频率成等比数列
C.“商、羽、角”的频率成等比数列
D.“徵、商、羽”的频率成等比数列
解:设“宫”的频率为a,由题意经过一次“损”,可得“徵”的频率为a,“徵”经过一次“益”,可得“商”的频率为a,
“商”经过一次“损”,可得“羽”频率为a,最后“羽”经过一次“益”,可得“角”的频率是a,
由于a,a,a成等比数列,所以“宫、商、角”的频率成等比数列,
故选:A.
6.(3分)若函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)图象的一条对称轴是( )
A.x= B.x=﹣ C.x= D.x=
解:根据函数f(x)=Asin(ωx+φ)的部分图象,
可得它的一个对称中心的横坐标为x==﹣,
故它的一条对称轴为 x==﹣,
另一条为 x==,
故选:B.
7.(3分)函数f(x)=ex﹣x2﹣2x的图象大致为( )
A. B.
C. D.
解:作出函数y=ex与函数y=x2+2x的图象如下图所示,
由图象可知,函数y=ex与函数y=x2+2x的图象有3个交点,则函数f(x)=ex﹣x2﹣2x有3个零点,
观察选项可知,只有选项B符合题意.
故选:B.
8.(3分)设实数k,已知函数f(x)=,若函数f(x)﹣k在区间(0,+∞)上有两个零点x1,x2(x1<x2),则(x2﹣x1)f(x1)的取值范围是( )
A.[1,e2] B.[﹣1,e) C.[e,e2) D.[2,e2)
解:画出函数f(x)图象如图所示:
令y=f(x)﹣k=0,可得f(x)=k,
即y=f(x)和y=k有两个不同的交点根据图象可知:
k∈[1,e),由e=x2﹣1=k得x1=lnk,x2=k+1,
所以(x2﹣x1)?f(x1)=k2+k﹣klnk,
构造函数h(k)=k2+k﹣klnk(k∈[1,e)),
由于h′(k)=2k﹣lnk,h″(k)=2﹣>0,k∈[1,e),
所以k∈[1,e)时h′(k)递增,因为h′(k)≥h′(1)=2>0,
所以h(k)在k∈[1,e)时递增,所以h(k)∈[2,e2),
故选:D.
9.(3分)某人退休前后各类支出情况如图,已知退休前工资收入为8000元/月,退休后每月储蓄的金额比退休前每月储蓄的金额少1500元,则下面结论中错误的是( )
A.该教师退休前每月储蓄支出2400元
B.该教师退休后的旅行支出是退休前旅行支出的3倍
C.该教师退休工资收入为6000元/月
D.该教师退休后的其他支出比退休前的其他支出少
解:∵退休前工资收入为8000元/月,每月储蓄的金额占30%,
则该教师退休前每月储蓄支出8000×30%=2400元,故A正确;
该教师退休后每月储蓄的金额比退休前每月储蓄的金额少1500元,
则该教师退休后每月储蓄的金额为900元,设该教师退休工资收入为x元/月,
则x?15%=900,即x=6000元/月,故C正确;
该教师退休前的旅行支出为8000×5%=400元,退休后的旅行支出为6000×15%=900元,
∴该教师退休后的旅行支出不是退休前旅行支出的3倍,故B错误;
该教师退休前的其他支出为8000×20%=1600元,退休后的其他支出为6000×25%=1500元,
∴该教师退休后的其他支出比退休前的其他支出少,故D正确.
故选:B.
10.(3分)在平面直角坐标系xOy中,已知双曲线C:=1(a>0,b>0)的焦点在圆O:x2+y2=20上,圆O与双曲线C的渐近线在第一、二象限分别交于M、N两点,若点E(0,3)满足ME⊥ON(O为坐标原点),下列说法正确的有( )
A.双曲线C的虚轴长为4
B.双曲线的离心率为
C.双曲线C的一条渐近线方程为y=x
D.三角形OMN的面积为8
解:令圆中y=0,可得x=±2,由题意可得双曲线的焦点坐标为:(±2,0),
且双曲线的渐近线的方程为:y=±x,代入圆的方程可得x2+x2=20,所以可得x=±=±,
由题意可得M(,),N(﹣,),
所以=(﹣,3﹣),=(﹣,),
因为ME⊥ON,所以?=0,
即(﹣,3﹣)?(﹣,)=0,
整理可得:﹣+=0,c=2=,
解得:b=4,a=2,
所以双曲线的方程为:﹣=1;
可得虚轴长为8,所以A不正确;
离心率e===,所以B正确;
渐近线的方程为:y=±2x,所以C不正确;
可得M(2,4),N(﹣2,4),
则S△MON=|MN|?yN=×4×4=8,
所以D正确,
故选:BD.
11.(3分)在正方体ABCD﹣A1B1C1D1中,AB=2,E、F分别为BB1、CD中点,P是BC1上的动点,则下列说法正确的有( )
A.A1F⊥AE
B.三棱锥P﹣AED1的体积与点P位置有关系
C.平面AED1截正方体ABCD﹣A1B1C1D的截面面积为
D.点A到平面AED1的距离为
解:A选项,取AB中点G,连接FG,A1G,记A1G与AE交点为O,
在正方体ABCD﹣A1B1C1D1中,AA1=AB,∠A1AG=∠ABE=,
因为E,F分别为BB1,CD中点,所以AG=BE,FG∥AD,
因此Rt△A1AG≌Rt△ABE,所以∠AA1G=∠BAE,∠A1GA=∠AEB,
因此∠OAG+∠OGA=∠BAE+∠A1GA=,因此∠AOG=,即AE⊥A1G,
又在正方体ABCD﹣A1B1C1D1中,AD⊥平面ABB1A1,所以FG⊥平面ABB1A1,
因为AE?平面ABB1A1,所以FG⊥AE,
又A1G∩FG=G,A1G?平面A1FG,所以A1F⊥AE,故A正确.
B选项,因为在正方体中AB∥C1D1,且AB=C1D1,
所以四边形ABC1D1为平行四边形,
因此BC1∥AD1,又BC1?平面AED1,AD1?平面AED1,
所以BC1∥平面AED1.
因此棱BC1上的所有点到平面AED1的距离都相等,
又P是棱BC1上的动点,
所以三棱锥P﹣AED1的体积始终为定值,故B错误.
C选项,取B1C1的中点M,连接EM,MD1,则EM∥BC1,且EM=BC1,
则EM∥AD1,
又正方体中,AB=2,所以MD1=AE==,
BC1=AD1=2,
因此EM=BC1=,
所以平面AED1截正方体ABCD﹣A1B1C1D1所得截面为等腰梯形EMD1A,
因此该等腰梯形的高为h===.
所以该截面的面积S=(AD1+EM)?h=,故C正确.
D选项,设点A1到平面AA1D1D的距离为d,
因为BB1∥平面AA1D1D,
所以点E到平面AA1D1D的距离为AB=2,
即点E到平面AA1D1的距离为2,
所以V=×2=??22?2=,
在△AED1中,AD1=2,AE=,ED1==3,
所以cos∠EAD1==,因此sin∠EAD1=,
所以S=?AD1?AE?sin∠EAD1=?2??=3,
又V=V=?S?d=,所以d=,
即点A1到平面AED1的距离为,故D错误.
故选:AC.
12.(3分)已知函数f(x)=+cosx﹣(x∈R),则下列说法错误的有( )
A.直线y=0为曲线y=f(x)的一条切线
B.f(x)的极值点个数为3
C.f(x)的零点个数为4
D.若f(x1)=f(x2)(x1≠x2),则x1+x2=0
解:∵f(x)=+cosx﹣(x∈R),
∴f′(x)=﹣sinx,令f′(x)=0,得sinx=,
画出函数y=和y=sinx的图象,如图1示:
,
显然x∈(,+∞),(﹣,0)时,f′(x)>0,f(x)递增,
x∈(0,),(﹣∞,﹣)时,f′(x)<0,f(x)递减,
f(0)=1﹣,f()=0,f(﹣)=0,
故f(x)的大致图象如图2示:
,
对于A:f′()=0,f()=0,
所以切线的方程为:y﹣f()=f′()(x﹣),即y=0,A正确;
对于B:结合图1,两函数y=和y=sinx的图象有3个交点,
故f′(x)=0有3个不同的解,即f(x)有3个极值点,故B正确;
对于C:x=,x=﹣为其2个零点,故C错误;
对于D:因为f(﹣x)==f(x),
所以f(x)为偶函数,
若f(x1)=f(x2),则f(x1)=f(x2)=f(﹣x2),
所以x1=﹣x2,即x1+x2=0,故D正确.
故选:C.
三、填空题
13.(3分)二项式(2x﹣)6的展开式中x3的系数为 240 .
解:二项式(2x﹣)6的展开式的通项公式为
Tr+1=?(2x)6﹣r?(﹣)r=26﹣r??(﹣1)r?x,
令6﹣=3可得r=2,
∴二项式(2x﹣)6的展开式中x3的系数为:(﹣1)2??24=240.
故答案为:240.
14.(3分)已知α、β均为锐角,且sinα=,cos(α+β)=,则cos2β= .
解:∵α、β均为锐角,且sinα=,故cosα===,
∴sin2α=2sinαcosα=,cos2α=2cos2α﹣1=.
∵cos(α+β)=,∴sin(α+β)==,
∴sin2(α+β)=2sin(α+β)cos(α+β)=,cos2(α+β)=2cos2(α+β)﹣1=,
则cos2β=cos[2(α+β)﹣2α]=cos2(α+β)cos2α+sin2(α+β)sin2α=×+=,
故答案为:.
15.(3分)设a,b为实数,对于任意的a≥2,关于x的不等式x≤eax+b(e为自然对数的底数)在实数域R上恒成立,则b的取值范围为 [﹣ln2﹣1,+∞) .
解:当x≤0时,x≤eax+b恒成立;
当x>0时,x≤eax+b即为lnx≤ax+b,
考虑函数y=lnx的图象和直线y=ax+b的平行线y=ax+t,
即b≥tmax,
当a≥2时,设直线y=ax+t与函数y=lnx相切,设切点为(m,lnm),
由y=lnx的导数为y′=,
可得=a,即am=1,am+t=lnm,即t=lnm﹣1,
由a≥2可得0<≤,即0<m≤,
则t≤﹣ln2﹣1,
故b的取值范围是[﹣ln2﹣1,+∞).
故答案为:[﹣ln2﹣1,+∞).
16.(3分)农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为 ;若该六面体内有一球,则该球表面积的最大值为 .
解:该六面体是由两个全等的正四面体组合而成,正四面体的棱长为,
如图,在棱长为的正四面体S﹣ABC中,
取BC中点D,连结SD、AD,
作SO⊥平面ABC,垂足O在AD上,
则AD=SD==,OD=AD=,SO==,
∴该六面体的体积:
V=2VS﹣ABC=2××××=.
当该六面体内有一球,且该球体积取最大值时,球心为O,且该球与SD相切,
过球心O作OE⊥SD,则OE就是球半径,
∵SO×OD=SD×OE,
∴球半径R=OE===,
∴该球表面积的最大值为:S球=4π?=.
故答案为:,.
三、解答题
17.在△ABC中,设内角A,B,C所对的边分别为a,b,c,已知bcosC+ccosB=﹣4cosA,a=2.
(1)求角A的值;
(2)若三角形ABC的面积为,求△ABC的周长.
解:(1)由余弦定理可得b?+c?==a=2=﹣4cosA,
即cosA=﹣,
由0<A<π,可得A=;
(2)S△ABC=bcsinA=bc?sin=bc=,
则bc=,
由余弦定理可得a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bc?cos
=(b+c)2﹣bc=4,
即b+c==,
则△ABC的周长为2+.
18.已知函数f(x)=ax(a为常数,a>0且a≠1)
(1)在下列条件中选择一个条件_____(仅填序号),使得以此条件可以推出数列{an}为等差数列,并说明理由;
①数列{f(an)}是首项为4,公比为2的等比数列;
②数列{f(an)}是首项为4,公差为2的等差数列;
③数列{f(an)}是首项为4,公比为2的等比数列的前n项和构成的数列;
(2)在(1)的选择下,若a=2,b=(n∈N*),求数列{an?bn}的前n项和Sn.
解:(1)若选条件①时:
由题设知:f(an)=4×2n﹣1=2n+1=a(a为常数,a>0且a≠1),则an=loga2n+1=(n+1)loga2,
又an+1﹣an=(n+2)loga2﹣(n+1)loga2=loga2为常数,
∴数列{an}是首项为2loga2,公差为loga2的等差数列,故选条件①;
若选条件②时:
由题设知:f(an)=4+2(n﹣1)=2n+2=a(a为常数,a>0且a≠1),则an=loga(2n+2),
又an+1﹣an=loga(2n+4)﹣loga(2n+2)=loga≠常数,此时数列{an}不是等差数列,故不能选条件②;
若选条件③时:
由题设知:f(an)==2n+2﹣4=a(a为常数,a>0且a≠1),则an=loga(2n+2﹣4),
又an+1﹣an=loga(2n+3﹣4)﹣loga(2n+2﹣4)=loga≠常数,此时数列{an}不是等差数列,故不能选条件③;
综合以上,知选条件①可以推出数列{an}为等差数列;
(2)由(1)知:an=(n+1)loga2,
又a=2,b=(n∈N*),∴anbn=,
∴Sn=++…+,
又Sn=+…++,
两式相减得:Sn=1+++…+﹣=1+﹣,
整理得:Sn=3﹣.
19.如图,在四棱台ABCD﹣A1B1C1D1中,底面ABCD是菱形,AA1=A1B1=AB=1,∠ABC=60°,AA1⊥平面ABCD,点E是棱BC上一点.
(1)若E是BC中点,求证:平面AD1E⊥平面CC1D1D;
(2)设二面角E﹣AD1﹣D的平面角为θ,且|cosθ|=,求线段CE的长.
【解答】(1)证明:取BC中点M,连接AM,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,∴AM⊥BC,
∴AM⊥AD,
又AA1⊥平面ABCD,
∴AM,AD,AA1两两垂直,
∵四棱台ABCD﹣A1B1C1D1,∴四边形ABCD∽四边形A1B1C1D1,
∴四边形A1B1C1D1是菱形,A1D1=A1B1=1,
以A为原点,以AM,AD,AA1为坐标轴建立空间直角坐标系A﹣xyz,如图所示,
则A(0,0,0),D(0,2,0),C(,1,0),D1(0,1,1),
若E为BC得中点,则E(,0,0),
∴=(,0,0),=(0,1,1),=(﹣,1,0),=(0,﹣1,1),
设平面AD1E的法向量为=(x1,y1,z1),则,即,
令z1=1可得=(0,﹣1,1),
设平面CDD1C1的法向量为=(x2,y2,z2),则,即,
令x2=1可得=(1,,),
∴=0﹣+=0,∴⊥,
∴平面平面AD1E⊥平面CC1D1D.
(2)解:设E(,m,0),﹣1≤m≤1,则=(,m,0),
设平面EAD1的法向量为=(x3,y3,z3),则,即,
令x3=m可得=(m,﹣,),
∵AM⊥平面ADD1A1,∴=(1,0,0)为平面ADD1的一个法向量,
∴cos<,>===,
∴|cosθ|==,解得m=±,
又CM=1,∴CE=1±.
20.第13届女排世界杯于2019年9月14日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球MIKSA﹣V200W,已知这种球的质量指标ξ(单位:g)服从正态分布N(270,52).比赛赛制采取单循环方式,即每支球队进行11场比赛(采取5局3胜制),最后靠积分选出最后冠军积分规则如下:比赛中以3:0或3:1取胜的球队积3分,负队积0分;而在比赛中以3:2取胜的球队积2分,负队积1分.已知第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为p(0<p<1).
(1)如果比赛准备了1000个排球,估计质量指标在(260,265]内的排球个数(计算结果取整数).
(2)第10轮比赛中,记中国队3:1取胜的概率为f(p).
(ⅰ)求出f(p)的最大值点p0;
(ⅱ)若以p0作为p的值记第10轮比赛中,中国队所得积分为X,求X的分布列.
参考数据:ξ~N(u,σ2),则p(μ﹣σ<X<μ+σ)≈0.6826,p(μ﹣2σ<X<μ+2σ)≈0.9644.
解:(1)∵ξ服从正态分布N(270,52),
∴P(260,275]===0.1359,
∴质量指标在(260,265]内的排球个数约为1000×0.1359≈136个;
(2)(ⅰ)前三场赢两场,第四场必赢,f(p)=C32p3(1﹣p),
因此f′(p)=3[3p2(1﹣p)+p3(﹣1)]=3p2(3﹣4p).
令f′(p)=0,得p=,
当p∈(0,)时,f′(p)>0,f(p)在(0,)上为增函数;
当p∈(,1)时,f′(p)<0,f(p)在(,1)上为减函数.
∴f(p)的最大值点p0=,
从而p0=,
(ⅱ)X的可能取值为3,2,1,0,
P(X=3)=()3+C32×()3×=,P(x=2)=C42×()3×()2=,
P(X=1)=C42×()2×()5=,
P(X=0)=()3+C31×()×()3=.
∴X的分布列:
X 3 2 1 0
P
21.设a为实数,已知函数f(x)=ex+ae﹣x+(1﹣a)x﹣2.
(1)当a=2时,求f(x)的单调区间;
(2)当a≥1时,若f(x)有两个不同的零点,求a的取值范围.
解:(1)a=2时,f(x)=ex+2e﹣x﹣x﹣2,
则f′(x)=ex﹣2e﹣x﹣1,f″(x)=ex+2e﹣x>0,
故f′(x)在R递增,而f′(ln2)=0,
故f(x)在(﹣∞,ln2)递减,在(ln2,+∞)递增;
(2)f(x)=ex+ae﹣x+(1﹣a)x﹣2,
则f′(x)=ex﹣ae﹣x+(1﹣a),f″(x)=ex+ae﹣x,
∵a≥1,∴f″(x)>0,f′(x)在R递增,
而f′(lna)=elna﹣ae﹣lna+1﹣a=0,
故f(x)在(﹣∞,lna)递减,在(lna,+∞)递增,
故f(x)min=f(lna)=a+1+(1﹣a)lna﹣2,
若f(x)有两个不同的零点,
则f(x)min=f(lna)=a+1+(1﹣a)lna﹣2<0,
解得:a>e,
故a的取值范围是(e,+∞).
22.在平面直角坐标系xOy中,已知椭圆C:=1(a>b>0)的离心率为,以椭圆上的一点和长轴的两个端点为顶点的三角形面积最大值为.
(1)求a,b的值;
(2)当过点P(6,0)的动直线l与椭圆C交于不同的点A,B时,在线段AB上取点Q,使得||?||=||?||,问:点Q是否总在某条定直线上?若是,求出该直线方程,若不是,说明理由.
解:(1)由题意,,解得,
∴a=2,b=;
(2)点Q总在直线x=上.
证明如下:由(1)可得,椭圆方程为.
由题意可得直线l的斜率存在,设直线l的方程为y=k(x﹣6),
代入椭圆方程,整理得(3+4k2)x2﹣48k2x+144k2﹣12=0,
设A(x1,y1),B(x2,y2),
则,,
设Q(x0,y0),由||?||=||?||,得:
(6﹣x1)(x0﹣x2)=(x1﹣x0)(6﹣x2)(考虑线段在x轴上的射影即可),
∴12x0=(6+x0)(x1+x2)﹣2x1x2,
于是,
整理得x0=,
∴点Q总在直线x=上.
一、选择题(共12小题).
1.(3分)已知集合M={x|(x﹣1)2<4,x∈R},N={﹣2,﹣1,0,1,2},则M∩N=( )
A.{0,1,2} B.{﹣1,0,1,2} C.{﹣1,0,2,3} D.{0,1,2,3}
2.(3分)设z=,则z的虚部为( )
A. B.﹣ C. D.﹣
3.(3分)已知m,n∈R,则“mn<0”是“抛物线mx2+ny=0的焦点在y轴正半轴上”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.(3分)设λ为实数,已知向量=(﹣1,2),=(1,λ).若⊥,则向量+2与之间的夹角为( )
A. B. C. D.
5.(3分)音乐与数学有着密切的联系,我国春秋时期有个著名的“三分损益法”:以“宫”为基本音,“宫”经过一次“损”,频率变为原来的,得到“徵”;“徵”经过一次“益”,频率变为原来的,得到“商”;…….依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶.据此可推得( )
A.“宫、商、角”的频率成等比数列
B.“宫、徵、商”的频率成等比数列
C.“商、羽、角”的频率成等比数列
D.“徵、商、羽”的频率成等比数列
6.(3分)若函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)图象的一条对称轴是( )
A.x= B.x=﹣ C.x= D.x=
7.(3分)函数f(x)=ex﹣x2﹣2x的图象大致为( )
A. B.
C. D.
8.(3分)设实数k,已知函数f(x)=,若函数f(x)﹣k在区间(0,+∞)上有两个零点x1,x2(x1<x2),则(x2﹣x1)f(x1)的取值范围是( )
A.[1,e2] B.[﹣1,e) C.[e,e2) D.[2,e2)
9.(3分)某人退休前后各类支出情况如图,已知退休前工资收入为8000元/月,退休后每月储蓄的金额比退休前每月储蓄的金额少1500元,则下面结论中错误的是( )
A.该教师退休前每月储蓄支出2400元
B.该教师退休后的旅行支出是退休前旅行支出的3倍
C.该教师退休工资收入为6000元/月
D.该教师退休后的其他支出比退休前的其他支出少
10.(3分)在平面直角坐标系xOy中,已知双曲线C:=1(a>0,b>0)的焦点在圆O:x2+y2=20上,圆O与双曲线C的渐近线在第一、二象限分别交于M、N两点,若点E(0,3)满足ME⊥ON(O为坐标原点),下列说法正确的有( )
A.双曲线C的虚轴长为4
B.双曲线的离心率为
C.双曲线C的一条渐近线方程为y=x
D.三角形OMN的面积为8
11.(3分)在正方体ABCD﹣A1B1C1D1中,AB=2,E、F分别为BB1、CD中点,P是BC1上的动点,则下列说法正确的有( )
A.A1F⊥AE
B.三棱锥P﹣AED1的体积与点P位置有关系
C.平面AED1截正方体ABCD﹣A1B1C1D的截面面积为
D.点A到平面AED1的距离为
12.(3分)已知函数f(x)=+cosx﹣(x∈R),则下列说法错误的有( )
A.直线y=0为曲线y=f(x)的一条切线
B.f(x)的极值点个数为3
C.f(x)的零点个数为4
D.若f(x1)=f(x2)(x1≠x2),则x1+x2=0
三、填空题(共4小题)
13.(3分)二项式(2x﹣)6的展开式中x3的系数为 .
14.(3分)已知α、β均为锐角,且sinα=,cos(α+β)=,则cos2β= .
15.(3分)设a,b为实数,对于任意的a≥2,关于x的不等式x≤eax+b(e为自然对数的底数)在实数域R上恒成立,则b的取值范围为 .
16.(3分)农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为 ;若该六面体内有一球,则该球表面积的最大值为 .
三、解答题
17.在△ABC中,设内角A,B,C所对的边分别为a,b,c,已知bcosC+ccosB=﹣4cosA,a=2.
(1)求角A的值;
(2)若三角形ABC的面积为,求△ABC的周长.
18.已知函数f(x)=ax(a为常数,a>0且a≠1)
(1)在下列条件中选择一个条件_____(仅填序号),使得以此条件可以推出数列{an}为等差数列,并说明理由;
①数列{f(an)}是首项为4,公比为2的等比数列;
②数列{f(an)}是首项为4,公差为2的等差数列;
③数列{f(an)}是首项为4,公比为2的等比数列的前n项和构成的数列;
(2)在(1)的选择下,若a=2,b=(n∈N*),求数列{an?bn}的前n项和Sn.
19.如图,在四棱台ABCD﹣A1B1C1D1中,底面ABCD是菱形,AA1=A1B1=AB=1,∠ABC=60°,AA1⊥平面ABCD,点E是棱BC上一点.
(1)若E是BC中点,求证:平面AD1E⊥平面CC1D1D;
(2)设二面角E﹣AD1﹣D的平面角为θ,且|cosθ|=,求线段CE的长.
20.第13届女排世界杯于2019年9月14日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球MIKSA﹣V200W,已知这种球的质量指标ξ(单位:g)服从正态分布N(270,52).比赛赛制采取单循环方式,即每支球队进行11场比赛(采取5局3胜制),最后靠积分选出最后冠军积分规则如下:比赛中以3:0或3:1取胜的球队积3分,负队积0分;而在比赛中以3:2取胜的球队积2分,负队积1分.已知第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为p(0<p<1).
(1)如果比赛准备了1000个排球,估计质量指标在(260,265]内的排球个数(计算结果取整数).
(2)第10轮比赛中,记中国队3:1取胜的概率为f(p).
(ⅰ)求出f(p)的最大值点p0;
(ⅱ)若以p0作为p的值记第10轮比赛中,中国队所得积分为X,求X的分布列.
参考数据:ξ~N(u,σ2),则p(μ﹣σ<X<μ+σ)≈0.6826,p(μ﹣2σ<X<μ+2σ)≈0.9644.
21.设a为实数,已知函数f(x)=ex+ae﹣x+(1﹣a)x﹣2.
(1)当a=2时,求f(x)的单调区间;
(2)当a≥1时,若f(x)有两个不同的零点,求a的取值范围.
22.在平面直角坐标系xOy中,已知椭圆C:=1(a>b>0)的离心率为,以椭圆上的一点和长轴的两个端点为顶点的三角形面积最大值为.
(1)求a,b的值;
(2)当过点P(6,0)的动直线l与椭圆C交于不同的点A,B时,在线段AB上取点Q,使得||?||=||?||,问:点Q是否总在某条定直线上?若是,求出该直线方程,若不是,说明理由.
参考答案
一、单项选择题
1.(3分)已知集合M={x|(x﹣1)2<4,x∈R},N={﹣2,﹣1,0,1,2},则M∩N=( )
A.{0,1,2} B.{﹣1,0,1,2} C.{﹣1,0,2,3} D.{0,1,2,3}
解:由M中不等式变形得:﹣2<x﹣1<2,
解得:﹣1<x<3,即M=(﹣1,3),
∵N={﹣2.﹣1,0,1,2},
∴M∩N={0,1,2}.
故选:A.
2.(3分)设z=,则z的虚部为( )
A. B.﹣ C. D.﹣
解:∵z====+i,
∴z的虚部为,
故选:A.
3.(3分)已知m,n∈R,则“mn<0”是“抛物线mx2+ny=0的焦点在y轴正半轴上”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解:抛物线mx2+ny=0的焦点在y轴正半轴上?>0,即mn<0,
∴“mn<0”是“抛物线mx2+ny=0的焦点在y轴正半轴上”的充要条件.
故选:C.
4.(3分)设λ为实数,已知向量=(﹣1,2),=(1,λ).若⊥,则向量+2与之间的夹角为( )
A. B. C. D.
解:λ为实数,已知向量=(﹣1,2),=(1,λ),
若⊥,则﹣1×1+2λ=0,解得λ=,
所以=(1,),+2=(1,3),
设+2与之间的夹角为θ,
则(+2)?=2+2?=5+0=5,
再根据(+2)?=|+2|?||?cosθ=??cosθ,
所以??cosθ=5,求得cosθ=,
由0≤θ≤π,
所以θ=,
故选:A.
5.(3分)音乐与数学有着密切的联系,我国春秋时期有个著名的“三分损益法”:以“宫”为基本音,“宫”经过一次“损”,频率变为原来的,得到“徵”;“徵”经过一次“益”,频率变为原来的,得到“商”;…….依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶.据此可推得( )
A.“宫、商、角”的频率成等比数列
B.“宫、徵、商”的频率成等比数列
C.“商、羽、角”的频率成等比数列
D.“徵、商、羽”的频率成等比数列
解:设“宫”的频率为a,由题意经过一次“损”,可得“徵”的频率为a,“徵”经过一次“益”,可得“商”的频率为a,
“商”经过一次“损”,可得“羽”频率为a,最后“羽”经过一次“益”,可得“角”的频率是a,
由于a,a,a成等比数列,所以“宫、商、角”的频率成等比数列,
故选:A.
6.(3分)若函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)图象的一条对称轴是( )
A.x= B.x=﹣ C.x= D.x=
解:根据函数f(x)=Asin(ωx+φ)的部分图象,
可得它的一个对称中心的横坐标为x==﹣,
故它的一条对称轴为 x==﹣,
另一条为 x==,
故选:B.
7.(3分)函数f(x)=ex﹣x2﹣2x的图象大致为( )
A. B.
C. D.
解:作出函数y=ex与函数y=x2+2x的图象如下图所示,
由图象可知,函数y=ex与函数y=x2+2x的图象有3个交点,则函数f(x)=ex﹣x2﹣2x有3个零点,
观察选项可知,只有选项B符合题意.
故选:B.
8.(3分)设实数k,已知函数f(x)=,若函数f(x)﹣k在区间(0,+∞)上有两个零点x1,x2(x1<x2),则(x2﹣x1)f(x1)的取值范围是( )
A.[1,e2] B.[﹣1,e) C.[e,e2) D.[2,e2)
解:画出函数f(x)图象如图所示:
令y=f(x)﹣k=0,可得f(x)=k,
即y=f(x)和y=k有两个不同的交点根据图象可知:
k∈[1,e),由e=x2﹣1=k得x1=lnk,x2=k+1,
所以(x2﹣x1)?f(x1)=k2+k﹣klnk,
构造函数h(k)=k2+k﹣klnk(k∈[1,e)),
由于h′(k)=2k﹣lnk,h″(k)=2﹣>0,k∈[1,e),
所以k∈[1,e)时h′(k)递增,因为h′(k)≥h′(1)=2>0,
所以h(k)在k∈[1,e)时递增,所以h(k)∈[2,e2),
故选:D.
9.(3分)某人退休前后各类支出情况如图,已知退休前工资收入为8000元/月,退休后每月储蓄的金额比退休前每月储蓄的金额少1500元,则下面结论中错误的是( )
A.该教师退休前每月储蓄支出2400元
B.该教师退休后的旅行支出是退休前旅行支出的3倍
C.该教师退休工资收入为6000元/月
D.该教师退休后的其他支出比退休前的其他支出少
解:∵退休前工资收入为8000元/月,每月储蓄的金额占30%,
则该教师退休前每月储蓄支出8000×30%=2400元,故A正确;
该教师退休后每月储蓄的金额比退休前每月储蓄的金额少1500元,
则该教师退休后每月储蓄的金额为900元,设该教师退休工资收入为x元/月,
则x?15%=900,即x=6000元/月,故C正确;
该教师退休前的旅行支出为8000×5%=400元,退休后的旅行支出为6000×15%=900元,
∴该教师退休后的旅行支出不是退休前旅行支出的3倍,故B错误;
该教师退休前的其他支出为8000×20%=1600元,退休后的其他支出为6000×25%=1500元,
∴该教师退休后的其他支出比退休前的其他支出少,故D正确.
故选:B.
10.(3分)在平面直角坐标系xOy中,已知双曲线C:=1(a>0,b>0)的焦点在圆O:x2+y2=20上,圆O与双曲线C的渐近线在第一、二象限分别交于M、N两点,若点E(0,3)满足ME⊥ON(O为坐标原点),下列说法正确的有( )
A.双曲线C的虚轴长为4
B.双曲线的离心率为
C.双曲线C的一条渐近线方程为y=x
D.三角形OMN的面积为8
解:令圆中y=0,可得x=±2,由题意可得双曲线的焦点坐标为:(±2,0),
且双曲线的渐近线的方程为:y=±x,代入圆的方程可得x2+x2=20,所以可得x=±=±,
由题意可得M(,),N(﹣,),
所以=(﹣,3﹣),=(﹣,),
因为ME⊥ON,所以?=0,
即(﹣,3﹣)?(﹣,)=0,
整理可得:﹣+=0,c=2=,
解得:b=4,a=2,
所以双曲线的方程为:﹣=1;
可得虚轴长为8,所以A不正确;
离心率e===,所以B正确;
渐近线的方程为:y=±2x,所以C不正确;
可得M(2,4),N(﹣2,4),
则S△MON=|MN|?yN=×4×4=8,
所以D正确,
故选:BD.
11.(3分)在正方体ABCD﹣A1B1C1D1中,AB=2,E、F分别为BB1、CD中点,P是BC1上的动点,则下列说法正确的有( )
A.A1F⊥AE
B.三棱锥P﹣AED1的体积与点P位置有关系
C.平面AED1截正方体ABCD﹣A1B1C1D的截面面积为
D.点A到平面AED1的距离为
解:A选项,取AB中点G,连接FG,A1G,记A1G与AE交点为O,
在正方体ABCD﹣A1B1C1D1中,AA1=AB,∠A1AG=∠ABE=,
因为E,F分别为BB1,CD中点,所以AG=BE,FG∥AD,
因此Rt△A1AG≌Rt△ABE,所以∠AA1G=∠BAE,∠A1GA=∠AEB,
因此∠OAG+∠OGA=∠BAE+∠A1GA=,因此∠AOG=,即AE⊥A1G,
又在正方体ABCD﹣A1B1C1D1中,AD⊥平面ABB1A1,所以FG⊥平面ABB1A1,
因为AE?平面ABB1A1,所以FG⊥AE,
又A1G∩FG=G,A1G?平面A1FG,所以A1F⊥AE,故A正确.
B选项,因为在正方体中AB∥C1D1,且AB=C1D1,
所以四边形ABC1D1为平行四边形,
因此BC1∥AD1,又BC1?平面AED1,AD1?平面AED1,
所以BC1∥平面AED1.
因此棱BC1上的所有点到平面AED1的距离都相等,
又P是棱BC1上的动点,
所以三棱锥P﹣AED1的体积始终为定值,故B错误.
C选项,取B1C1的中点M,连接EM,MD1,则EM∥BC1,且EM=BC1,
则EM∥AD1,
又正方体中,AB=2,所以MD1=AE==,
BC1=AD1=2,
因此EM=BC1=,
所以平面AED1截正方体ABCD﹣A1B1C1D1所得截面为等腰梯形EMD1A,
因此该等腰梯形的高为h===.
所以该截面的面积S=(AD1+EM)?h=,故C正确.
D选项,设点A1到平面AA1D1D的距离为d,
因为BB1∥平面AA1D1D,
所以点E到平面AA1D1D的距离为AB=2,
即点E到平面AA1D1的距离为2,
所以V=×2=??22?2=,
在△AED1中,AD1=2,AE=,ED1==3,
所以cos∠EAD1==,因此sin∠EAD1=,
所以S=?AD1?AE?sin∠EAD1=?2??=3,
又V=V=?S?d=,所以d=,
即点A1到平面AED1的距离为,故D错误.
故选:AC.
12.(3分)已知函数f(x)=+cosx﹣(x∈R),则下列说法错误的有( )
A.直线y=0为曲线y=f(x)的一条切线
B.f(x)的极值点个数为3
C.f(x)的零点个数为4
D.若f(x1)=f(x2)(x1≠x2),则x1+x2=0
解:∵f(x)=+cosx﹣(x∈R),
∴f′(x)=﹣sinx,令f′(x)=0,得sinx=,
画出函数y=和y=sinx的图象,如图1示:
,
显然x∈(,+∞),(﹣,0)时,f′(x)>0,f(x)递增,
x∈(0,),(﹣∞,﹣)时,f′(x)<0,f(x)递减,
f(0)=1﹣,f()=0,f(﹣)=0,
故f(x)的大致图象如图2示:
,
对于A:f′()=0,f()=0,
所以切线的方程为:y﹣f()=f′()(x﹣),即y=0,A正确;
对于B:结合图1,两函数y=和y=sinx的图象有3个交点,
故f′(x)=0有3个不同的解,即f(x)有3个极值点,故B正确;
对于C:x=,x=﹣为其2个零点,故C错误;
对于D:因为f(﹣x)==f(x),
所以f(x)为偶函数,
若f(x1)=f(x2),则f(x1)=f(x2)=f(﹣x2),
所以x1=﹣x2,即x1+x2=0,故D正确.
故选:C.
三、填空题
13.(3分)二项式(2x﹣)6的展开式中x3的系数为 240 .
解:二项式(2x﹣)6的展开式的通项公式为
Tr+1=?(2x)6﹣r?(﹣)r=26﹣r??(﹣1)r?x,
令6﹣=3可得r=2,
∴二项式(2x﹣)6的展开式中x3的系数为:(﹣1)2??24=240.
故答案为:240.
14.(3分)已知α、β均为锐角,且sinα=,cos(α+β)=,则cos2β= .
解:∵α、β均为锐角,且sinα=,故cosα===,
∴sin2α=2sinαcosα=,cos2α=2cos2α﹣1=.
∵cos(α+β)=,∴sin(α+β)==,
∴sin2(α+β)=2sin(α+β)cos(α+β)=,cos2(α+β)=2cos2(α+β)﹣1=,
则cos2β=cos[2(α+β)﹣2α]=cos2(α+β)cos2α+sin2(α+β)sin2α=×+=,
故答案为:.
15.(3分)设a,b为实数,对于任意的a≥2,关于x的不等式x≤eax+b(e为自然对数的底数)在实数域R上恒成立,则b的取值范围为 [﹣ln2﹣1,+∞) .
解:当x≤0时,x≤eax+b恒成立;
当x>0时,x≤eax+b即为lnx≤ax+b,
考虑函数y=lnx的图象和直线y=ax+b的平行线y=ax+t,
即b≥tmax,
当a≥2时,设直线y=ax+t与函数y=lnx相切,设切点为(m,lnm),
由y=lnx的导数为y′=,
可得=a,即am=1,am+t=lnm,即t=lnm﹣1,
由a≥2可得0<≤,即0<m≤,
则t≤﹣ln2﹣1,
故b的取值范围是[﹣ln2﹣1,+∞).
故答案为:[﹣ln2﹣1,+∞).
16.(3分)农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为 ;若该六面体内有一球,则该球表面积的最大值为 .
解:该六面体是由两个全等的正四面体组合而成,正四面体的棱长为,
如图,在棱长为的正四面体S﹣ABC中,
取BC中点D,连结SD、AD,
作SO⊥平面ABC,垂足O在AD上,
则AD=SD==,OD=AD=,SO==,
∴该六面体的体积:
V=2VS﹣ABC=2××××=.
当该六面体内有一球,且该球体积取最大值时,球心为O,且该球与SD相切,
过球心O作OE⊥SD,则OE就是球半径,
∵SO×OD=SD×OE,
∴球半径R=OE===,
∴该球表面积的最大值为:S球=4π?=.
故答案为:,.
三、解答题
17.在△ABC中,设内角A,B,C所对的边分别为a,b,c,已知bcosC+ccosB=﹣4cosA,a=2.
(1)求角A的值;
(2)若三角形ABC的面积为,求△ABC的周长.
解:(1)由余弦定理可得b?+c?==a=2=﹣4cosA,
即cosA=﹣,
由0<A<π,可得A=;
(2)S△ABC=bcsinA=bc?sin=bc=,
则bc=,
由余弦定理可得a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bc?cos
=(b+c)2﹣bc=4,
即b+c==,
则△ABC的周长为2+.
18.已知函数f(x)=ax(a为常数,a>0且a≠1)
(1)在下列条件中选择一个条件_____(仅填序号),使得以此条件可以推出数列{an}为等差数列,并说明理由;
①数列{f(an)}是首项为4,公比为2的等比数列;
②数列{f(an)}是首项为4,公差为2的等差数列;
③数列{f(an)}是首项为4,公比为2的等比数列的前n项和构成的数列;
(2)在(1)的选择下,若a=2,b=(n∈N*),求数列{an?bn}的前n项和Sn.
解:(1)若选条件①时:
由题设知:f(an)=4×2n﹣1=2n+1=a(a为常数,a>0且a≠1),则an=loga2n+1=(n+1)loga2,
又an+1﹣an=(n+2)loga2﹣(n+1)loga2=loga2为常数,
∴数列{an}是首项为2loga2,公差为loga2的等差数列,故选条件①;
若选条件②时:
由题设知:f(an)=4+2(n﹣1)=2n+2=a(a为常数,a>0且a≠1),则an=loga(2n+2),
又an+1﹣an=loga(2n+4)﹣loga(2n+2)=loga≠常数,此时数列{an}不是等差数列,故不能选条件②;
若选条件③时:
由题设知:f(an)==2n+2﹣4=a(a为常数,a>0且a≠1),则an=loga(2n+2﹣4),
又an+1﹣an=loga(2n+3﹣4)﹣loga(2n+2﹣4)=loga≠常数,此时数列{an}不是等差数列,故不能选条件③;
综合以上,知选条件①可以推出数列{an}为等差数列;
(2)由(1)知:an=(n+1)loga2,
又a=2,b=(n∈N*),∴anbn=,
∴Sn=++…+,
又Sn=+…++,
两式相减得:Sn=1+++…+﹣=1+﹣,
整理得:Sn=3﹣.
19.如图,在四棱台ABCD﹣A1B1C1D1中,底面ABCD是菱形,AA1=A1B1=AB=1,∠ABC=60°,AA1⊥平面ABCD,点E是棱BC上一点.
(1)若E是BC中点,求证:平面AD1E⊥平面CC1D1D;
(2)设二面角E﹣AD1﹣D的平面角为θ,且|cosθ|=,求线段CE的长.
【解答】(1)证明:取BC中点M,连接AM,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,∴AM⊥BC,
∴AM⊥AD,
又AA1⊥平面ABCD,
∴AM,AD,AA1两两垂直,
∵四棱台ABCD﹣A1B1C1D1,∴四边形ABCD∽四边形A1B1C1D1,
∴四边形A1B1C1D1是菱形,A1D1=A1B1=1,
以A为原点,以AM,AD,AA1为坐标轴建立空间直角坐标系A﹣xyz,如图所示,
则A(0,0,0),D(0,2,0),C(,1,0),D1(0,1,1),
若E为BC得中点,则E(,0,0),
∴=(,0,0),=(0,1,1),=(﹣,1,0),=(0,﹣1,1),
设平面AD1E的法向量为=(x1,y1,z1),则,即,
令z1=1可得=(0,﹣1,1),
设平面CDD1C1的法向量为=(x2,y2,z2),则,即,
令x2=1可得=(1,,),
∴=0﹣+=0,∴⊥,
∴平面平面AD1E⊥平面CC1D1D.
(2)解:设E(,m,0),﹣1≤m≤1,则=(,m,0),
设平面EAD1的法向量为=(x3,y3,z3),则,即,
令x3=m可得=(m,﹣,),
∵AM⊥平面ADD1A1,∴=(1,0,0)为平面ADD1的一个法向量,
∴cos<,>===,
∴|cosθ|==,解得m=±,
又CM=1,∴CE=1±.
20.第13届女排世界杯于2019年9月14日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球MIKSA﹣V200W,已知这种球的质量指标ξ(单位:g)服从正态分布N(270,52).比赛赛制采取单循环方式,即每支球队进行11场比赛(采取5局3胜制),最后靠积分选出最后冠军积分规则如下:比赛中以3:0或3:1取胜的球队积3分,负队积0分;而在比赛中以3:2取胜的球队积2分,负队积1分.已知第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为p(0<p<1).
(1)如果比赛准备了1000个排球,估计质量指标在(260,265]内的排球个数(计算结果取整数).
(2)第10轮比赛中,记中国队3:1取胜的概率为f(p).
(ⅰ)求出f(p)的最大值点p0;
(ⅱ)若以p0作为p的值记第10轮比赛中,中国队所得积分为X,求X的分布列.
参考数据:ξ~N(u,σ2),则p(μ﹣σ<X<μ+σ)≈0.6826,p(μ﹣2σ<X<μ+2σ)≈0.9644.
解:(1)∵ξ服从正态分布N(270,52),
∴P(260,275]===0.1359,
∴质量指标在(260,265]内的排球个数约为1000×0.1359≈136个;
(2)(ⅰ)前三场赢两场,第四场必赢,f(p)=C32p3(1﹣p),
因此f′(p)=3[3p2(1﹣p)+p3(﹣1)]=3p2(3﹣4p).
令f′(p)=0,得p=,
当p∈(0,)时,f′(p)>0,f(p)在(0,)上为增函数;
当p∈(,1)时,f′(p)<0,f(p)在(,1)上为减函数.
∴f(p)的最大值点p0=,
从而p0=,
(ⅱ)X的可能取值为3,2,1,0,
P(X=3)=()3+C32×()3×=,P(x=2)=C42×()3×()2=,
P(X=1)=C42×()2×()5=,
P(X=0)=()3+C31×()×()3=.
∴X的分布列:
X 3 2 1 0
P
21.设a为实数,已知函数f(x)=ex+ae﹣x+(1﹣a)x﹣2.
(1)当a=2时,求f(x)的单调区间;
(2)当a≥1时,若f(x)有两个不同的零点,求a的取值范围.
解:(1)a=2时,f(x)=ex+2e﹣x﹣x﹣2,
则f′(x)=ex﹣2e﹣x﹣1,f″(x)=ex+2e﹣x>0,
故f′(x)在R递增,而f′(ln2)=0,
故f(x)在(﹣∞,ln2)递减,在(ln2,+∞)递增;
(2)f(x)=ex+ae﹣x+(1﹣a)x﹣2,
则f′(x)=ex﹣ae﹣x+(1﹣a),f″(x)=ex+ae﹣x,
∵a≥1,∴f″(x)>0,f′(x)在R递增,
而f′(lna)=elna﹣ae﹣lna+1﹣a=0,
故f(x)在(﹣∞,lna)递减,在(lna,+∞)递增,
故f(x)min=f(lna)=a+1+(1﹣a)lna﹣2,
若f(x)有两个不同的零点,
则f(x)min=f(lna)=a+1+(1﹣a)lna﹣2<0,
解得:a>e,
故a的取值范围是(e,+∞).
22.在平面直角坐标系xOy中,已知椭圆C:=1(a>b>0)的离心率为,以椭圆上的一点和长轴的两个端点为顶点的三角形面积最大值为.
(1)求a,b的值;
(2)当过点P(6,0)的动直线l与椭圆C交于不同的点A,B时,在线段AB上取点Q,使得||?||=||?||,问:点Q是否总在某条定直线上?若是,求出该直线方程,若不是,说明理由.
解:(1)由题意,,解得,
∴a=2,b=;
(2)点Q总在直线x=上.
证明如下:由(1)可得,椭圆方程为.
由题意可得直线l的斜率存在,设直线l的方程为y=k(x﹣6),
代入椭圆方程,整理得(3+4k2)x2﹣48k2x+144k2﹣12=0,
设A(x1,y1),B(x2,y2),
则,,
设Q(x0,y0),由||?||=||?||,得:
(6﹣x1)(x0﹣x2)=(x1﹣x0)(6﹣x2)(考虑线段在x轴上的射影即可),
∴12x0=(6+x0)(x1+x2)﹣2x1x2,
于是,
整理得x0=,
∴点Q总在直线x=上.
同课章节目录
