命题
图片预览





文档简介
(共18张PPT)
事例:主人邀请张三、李四、王五三个人吃饭聊天,时间到了,只有张三和李四两人准时赶到,王五打来电话说:“临时有急事,不能来了。”主人听了随口说了句:“你看看,该来的没有来。”张三听了,脸色一沉,起来一声不吭地走了;主人愣了片刻,又道:“哎,不该走的又走了。”李四听了大怒,拂袖而去。你能用逻辑学原理解释这两人离去的原因吗?
这就是今天我们来学习常用逻辑用语
命题
(1) 12>5; (2) 3是12的约数;
(3) 0.5是整数吗? (4)请把门关上!
(5)3 能被2整除; (6)2+4=7
(7)今天天气真好啊! (8)对顶角相等;
观察下列语句的特点
问1:哪几个语句是陈述句?
问3:哪几个语句能判断为假?
问2:哪几个语句能判断为真?
(1)、(2)、(5)、(6)、(8)
(1)、(2)、(8)
(5)、(6)
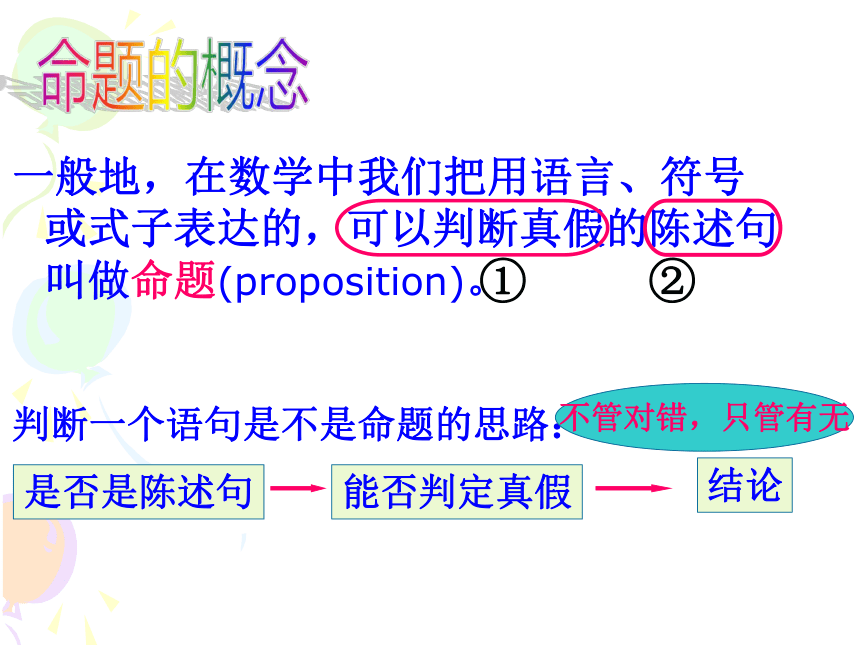
一般地,在数学中我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题(proposition)。
①
②
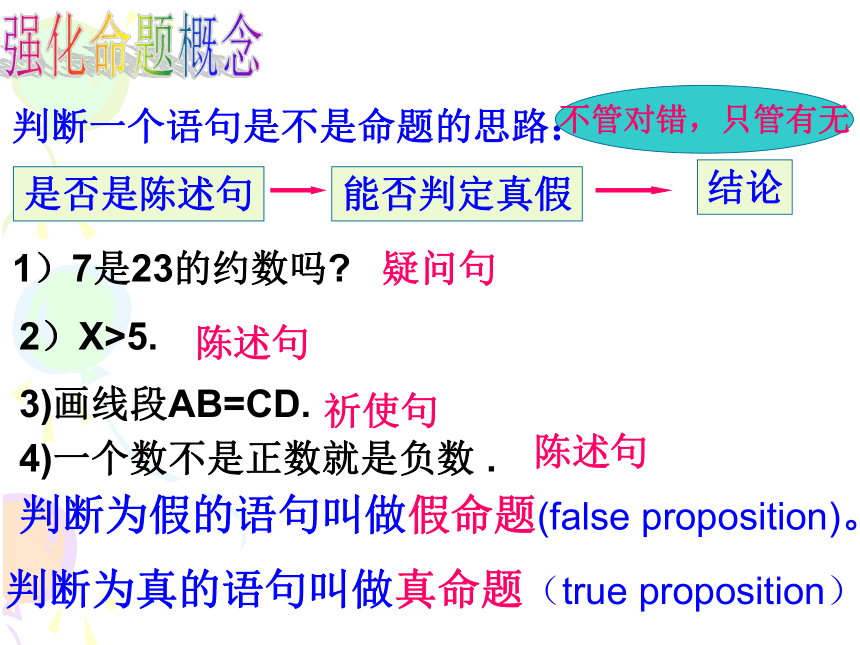
判断一个语句是不是命题的思路:
是否是陈述句
能否判定真假
结论
不管对错,只管有无
1)7是23的约数吗
陈述句
3)画线段AB=CD.
2)X>5.
疑问句
祈使句
4)一个数不是正数就是负数 .
陈述句
判断为假的语句叫做假命题(false proposition)。
判断为真的语句叫做真命题(true proposition)。
判断一个语句是不是命题的思路:
是否是陈述句
能否判定真假
结论
不管对错,只管有无
课本4页 练习 2
(1)空集是任何集合的子集;
真命题
真命题
假命题
假命题
上面(2)(4)具有“若p,则q”的形式.在数学中,这种形式的命题是常见的
“若p,则q”也可写成“如果p,那么q”“只要p,就有q”等形式.
其中p叫做命题的条件,q叫做命题的结论.
例1 判断下列语句中哪些是命题?是真命题还是假命题?
真命题
是
是
不是命题
是
是
是
(7)15>4.
(6)x>15.
(4)若空间中两条直线不相交,则这两条直线平行;
(3)指数函数是增函数吗?
(2)若整数a是素数,则a是奇数;
(5)
不是命题
下面来研究命题的“若p,则q”形式
命题的常见形式:
“若p,则q”形式
“若p则q”形式的命题
命题“若整数a是素数,则a是奇数。”具有“若p则q”的形式。
q
p
通常,我们把这种形式的命题中的p叫做命题的条件,q叫做命题的结论。
“若p则q”形式的命题是命题的一种形式而不是唯一的形式,也可写成“如果p,那么q” “只要p,就有q”等形式。
1)条件p:整数a能被2整除
结论q:整数a 是偶数。
解:
2)条件p:四边形是菱形
结论q:四边形的对角线互相垂直平分
例2. 指出下列命题的条件p和结论q
1)若整数a能被2整除,则a是偶数;
2)若四边形是菱形,则它的对角线互相
垂直且平分。
“若p则q”形式的命题的书写
对于一些条件与结论不明显的命题,一般采取先添补一些命题中省略的词句, 确定条件与结论。
如命题:“垂直于同一条直线的两个平面平行”。
写成“若p则q”的形式为:
若两个平面垂直于同一条直线,则这两个平面平行。
相等
对顶角
改写成:
若两个角是对顶角,则这两
个角相等。
(两个角是)
条件:
(补上适当词语)
结论:
角
两个
对顶角相等
(1)
方法:
先结论,
后条件
例3 把下列命题改写成“若……则……”的形式,并判断真假:
两条边相等
两个角相等
(2)在同一个三角形中,等角对等边
改写成:
同一个三角形中
条件:
(补上适当的词语)
结论:
这两个角所对的
在同一个三角形中,若两个角相等,则这两个角所对的边也相等。
例3 把下列命题改写成“若……则……”的形式,并判断真假:
把下列命题改写“若……则……”的形式,并判断真假:
(1)方程x2+2x-3=0是一元二次方程;
(2)垂直于同一条直线的两条直线平行;
(3)当a>0时,函数y=ax+b的值随着x的值的增加而增加;
若两条直线垂直于同一条直线,则这两条直线平行。
当a>0时,若x的值的增加,则函数y=ax+b的值也随着增加;
若一个方程是x2+2x-3=0,则这个方程是一元二次方程。
课本4页 练习 3
1.把下列命题改写成“若……则……”的形式,并判断真假:
(1)6是12和24的最大公约数;
(2)弦的垂直平分线经过圆心,并平分弦所对的弧;
事例:主人邀请张三、李四、王五三个人吃饭聊天,时间到了,只有张三和李四两人准时赶到,王五打来电话说:“临时有急事,不能来了。”主人听了随口说了句:“你看看,该来的没有来。”张三听了,脸色一沉,起来一声不吭地走了;主人愣了片刻,又道:“哎,不该走的又走了。”李四听了大怒,拂袖而去。你能用逻辑学原理解释这两人离去的原因吗?
这就是今天我们来学习常用逻辑用语
命题
(1) 12>5; (2) 3是12的约数;
(3) 0.5是整数吗? (4)请把门关上!
(5)3 能被2整除; (6)2+4=7
(7)今天天气真好啊! (8)对顶角相等;
观察下列语句的特点
问1:哪几个语句是陈述句?
问3:哪几个语句能判断为假?
问2:哪几个语句能判断为真?
(1)、(2)、(5)、(6)、(8)
(1)、(2)、(8)
(5)、(6)
一般地,在数学中我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题(proposition)。
①
②
判断一个语句是不是命题的思路:
是否是陈述句
能否判定真假
结论
不管对错,只管有无
1)7是23的约数吗
陈述句
3)画线段AB=CD.
2)X>5.
疑问句
祈使句
4)一个数不是正数就是负数 .
陈述句
判断为假的语句叫做假命题(false proposition)。
判断为真的语句叫做真命题(true proposition)。
判断一个语句是不是命题的思路:
是否是陈述句
能否判定真假
结论
不管对错,只管有无
课本4页 练习 2
(1)空集是任何集合的子集;
真命题
真命题
假命题
假命题
上面(2)(4)具有“若p,则q”的形式.在数学中,这种形式的命题是常见的
“若p,则q”也可写成“如果p,那么q”“只要p,就有q”等形式.
其中p叫做命题的条件,q叫做命题的结论.
例1 判断下列语句中哪些是命题?是真命题还是假命题?
真命题
是
是
不是命题
是
是
是
(7)15>4.
(6)x>15.
(4)若空间中两条直线不相交,则这两条直线平行;
(3)指数函数是增函数吗?
(2)若整数a是素数,则a是奇数;
(5)
不是命题
下面来研究命题的“若p,则q”形式
命题的常见形式:
“若p,则q”形式
“若p则q”形式的命题
命题“若整数a是素数,则a是奇数。”具有“若p则q”的形式。
q
p
通常,我们把这种形式的命题中的p叫做命题的条件,q叫做命题的结论。
“若p则q”形式的命题是命题的一种形式而不是唯一的形式,也可写成“如果p,那么q” “只要p,就有q”等形式。
1)条件p:整数a能被2整除
结论q:整数a 是偶数。
解:
2)条件p:四边形是菱形
结论q:四边形的对角线互相垂直平分
例2. 指出下列命题的条件p和结论q
1)若整数a能被2整除,则a是偶数;
2)若四边形是菱形,则它的对角线互相
垂直且平分。
“若p则q”形式的命题的书写
对于一些条件与结论不明显的命题,一般采取先添补一些命题中省略的词句, 确定条件与结论。
如命题:“垂直于同一条直线的两个平面平行”。
写成“若p则q”的形式为:
若两个平面垂直于同一条直线,则这两个平面平行。
相等
对顶角
改写成:
若两个角是对顶角,则这两
个角相等。
(两个角是)
条件:
(补上适当词语)
结论:
角
两个
对顶角相等
(1)
方法:
先结论,
后条件
例3 把下列命题改写成“若……则……”的形式,并判断真假:
两条边相等
两个角相等
(2)在同一个三角形中,等角对等边
改写成:
同一个三角形中
条件:
(补上适当的词语)
结论:
这两个角所对的
在同一个三角形中,若两个角相等,则这两个角所对的边也相等。
例3 把下列命题改写成“若……则……”的形式,并判断真假:
把下列命题改写“若……则……”的形式,并判断真假:
(1)方程x2+2x-3=0是一元二次方程;
(2)垂直于同一条直线的两条直线平行;
(3)当a>0时,函数y=ax+b的值随着x的值的增加而增加;
若两条直线垂直于同一条直线,则这两条直线平行。
当a>0时,若x的值的增加,则函数y=ax+b的值也随着增加;
若一个方程是x2+2x-3=0,则这个方程是一元二次方程。
课本4页 练习 3
1.把下列命题改写成“若……则……”的形式,并判断真假:
(1)6是12和24的最大公约数;
(2)弦的垂直平分线经过圆心,并平分弦所对的弧;
