四种命题间的相互关系
图片预览






文档简介
(共32张PPT)
新课讲授
(1)和(2)这样的两个命题叫做互
逆命题,(1)和(2)这样的两个命题叫
做互否命题,(1)和(4)这样的两个命
题叫做互为逆否命题.
总 结:
新课讲授
问题2:一个命题的逆命题、否命题与逆否
命题之间是否还存在着一定的关系呢?
新课讲授
新课讲授
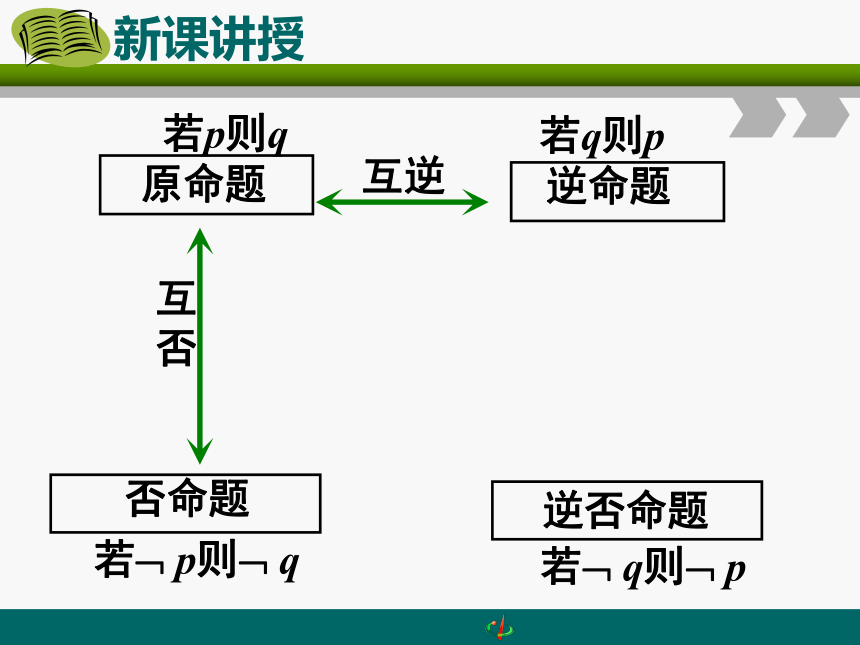
原命题
逆命题
否命题
逆否命题
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
原命题
逆命题
否命题
逆否命题
互逆
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
原命题
逆命题
否命题
逆否命题
互
否
互逆
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
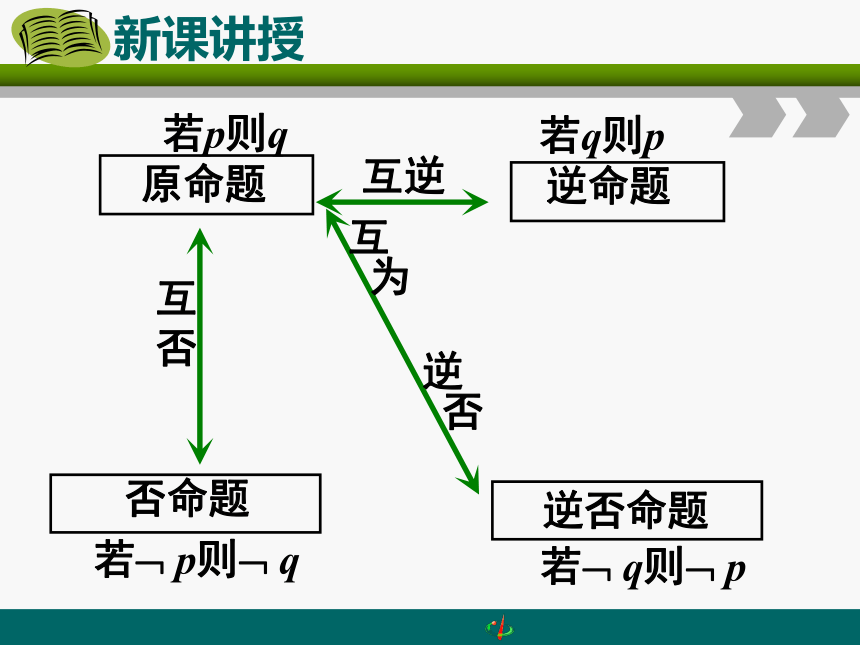
原命题
逆命题
否命题
逆否命题
互
否
互逆
互
为
逆
否
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
原命题
逆命题
否命题
逆否命题
互
否
互
否
互逆
若p则q
若q则p
若 p则 q
若 q则 p
互
为
逆
否
新课讲授
原命题
逆命题
否命题
逆否命题
互
否
互
否
互逆
互逆
若p则q
若q则p
若 p则 q
若 q则 p
互
为
逆
否
新课讲授
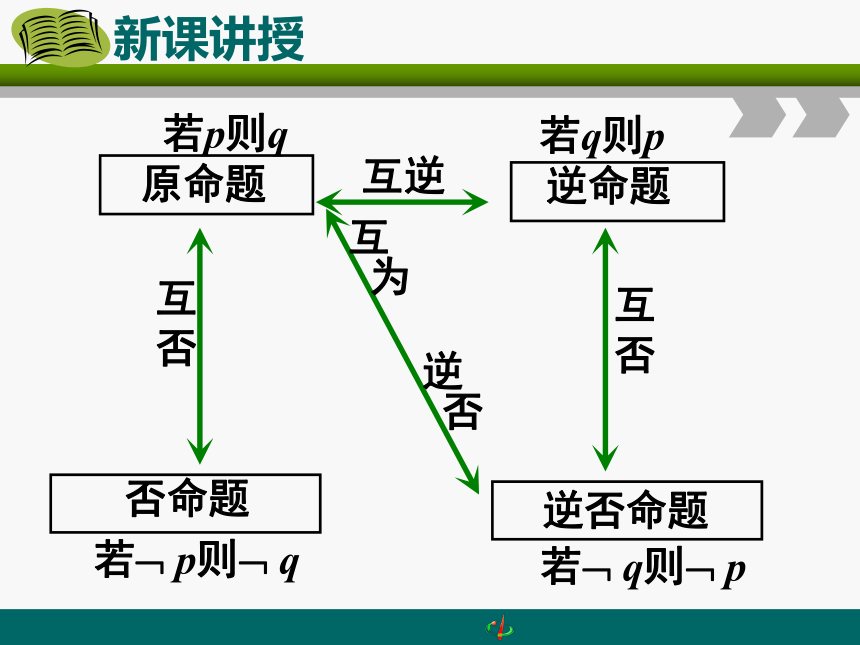
原命题
逆命题
否命题
逆否命题
互
否
互
否
互逆
互逆
互
为
逆
否
为
互
否
逆
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
问题3:原命题的真假与其它三种命题的真
假有什么关系?
结 论 1
原命题的真假和逆命题的真假没有关系。
原命题与逆命题之间的真假关系
结 论 2
原命题的真假和否命题的真假没有关系。
原命题与否命题之间的真假关系
结 论 3
原命题和逆否命题总是同真同假。
原命题与逆否命题之间的真假关系
否命题:若a≤b,则a+c≤b+c
逆命题:若a+c>b+c,则a>b
否命题:若四边形是不正方形,则四边形两对角线不垂直。
逆命题:若四边形两对角线垂直,则四边形是正方形。
真
真
假
假
观察下列命题的真假,并总结规律。
否命题与逆命题之间的真假关系
原命题:若a>b,则a+c>b+c
真
原命题:若四边形是正方形,则四边形两对角线垂直。
真
否命题:若a≤b,则ac2≤bc2
逆命题:若ac2>bc2,则a>b
否命题:若四边形对角线不相等,则四边形不是平行四边形。
逆命题:若四边形是平行四边形,则四边形对角线相等。
真
真
假
假
观察下列命题的真假,并总结规律。
否命题与逆命题之间的真假关系
原命题:若a>b,则ac2>bc2
假
原命题:若四边形对角线相等,则四边形是平行四边形。
假
结 论 4
逆命题和否命题总是同真同假。
否命题与逆命题之间的真假关系
一般的,四种命题的真假性,有且仅有以下四种情况:
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
四种命题的真假性之间的关系:
两个命题互为逆否命题,它们同真同假;
两个命题为互逆或互否命题,它们的真假性没有关系.
四种命题
原命题
逆命题
否命题
逆否命题
真假一致
真假
一致
若 p则 q
若 q则 p
若 p则 q
若 q则 p
课本 第8页 练习
总结
反证法:
要证明某一结论A是正确的,但不直接证明,而是先去证明A的反面(非A)是错误的,从而断定A是正确的。
即反证法就是通过否定命题的结论而导出矛盾来达到肯定命题的结论,完成命题的论证的一种数学证明方法。
反证法的步骤:
假设命题的结论不成立,即假设结论的反面成立。
从这个假设出发,通过推理论证,得出矛盾。
由矛盾判定假设不正确,从而肯定命题的结论正确。
推理过程中一定要用到才行
显而易见的矛盾(如和已知条件矛盾).
可能出现矛盾四种情况:
与题设矛盾;
与反设矛盾;
与公理、定理矛盾;
在证明过程中,推出自相矛盾的结论。
(课本8页B组).证明:圆的两条不是直径的相交弦不能互相平分.
.O
P
A
B
C
D
已知:在⊙O中,弦AB、CD相交于P,且AB、CD不是直径.
求证:弦AB、CD不被P平分
证明:
假设弦AB、CD被P平分,
则P是AB、CD 的中点,
连接OP,
由垂径定理的推论,可得:
OP⊥AB,OP⊥CD.
这与“在平面上过一点有且只有一条直线与已知直线垂直”相矛盾.
∴弦AB、CD不被P平分.
新课讲授
(1)和(2)这样的两个命题叫做互
逆命题,(1)和(2)这样的两个命题叫
做互否命题,(1)和(4)这样的两个命
题叫做互为逆否命题.
总 结:
新课讲授
问题2:一个命题的逆命题、否命题与逆否
命题之间是否还存在着一定的关系呢?
新课讲授
新课讲授
原命题
逆命题
否命题
逆否命题
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
原命题
逆命题
否命题
逆否命题
互逆
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
原命题
逆命题
否命题
逆否命题
互
否
互逆
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
原命题
逆命题
否命题
逆否命题
互
否
互逆
互
为
逆
否
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
原命题
逆命题
否命题
逆否命题
互
否
互
否
互逆
若p则q
若q则p
若 p则 q
若 q则 p
互
为
逆
否
新课讲授
原命题
逆命题
否命题
逆否命题
互
否
互
否
互逆
互逆
若p则q
若q则p
若 p则 q
若 q则 p
互
为
逆
否
新课讲授
原命题
逆命题
否命题
逆否命题
互
否
互
否
互逆
互逆
互
为
逆
否
为
互
否
逆
若p则q
若q则p
若 p则 q
若 q则 p
新课讲授
问题3:原命题的真假与其它三种命题的真
假有什么关系?
结 论 1
原命题的真假和逆命题的真假没有关系。
原命题与逆命题之间的真假关系
结 论 2
原命题的真假和否命题的真假没有关系。
原命题与否命题之间的真假关系
结 论 3
原命题和逆否命题总是同真同假。
原命题与逆否命题之间的真假关系
否命题:若a≤b,则a+c≤b+c
逆命题:若a+c>b+c,则a>b
否命题:若四边形是不正方形,则四边形两对角线不垂直。
逆命题:若四边形两对角线垂直,则四边形是正方形。
真
真
假
假
观察下列命题的真假,并总结规律。
否命题与逆命题之间的真假关系
原命题:若a>b,则a+c>b+c
真
原命题:若四边形是正方形,则四边形两对角线垂直。
真
否命题:若a≤b,则ac2≤bc2
逆命题:若ac2>bc2,则a>b
否命题:若四边形对角线不相等,则四边形不是平行四边形。
逆命题:若四边形是平行四边形,则四边形对角线相等。
真
真
假
假
观察下列命题的真假,并总结规律。
否命题与逆命题之间的真假关系
原命题:若a>b,则ac2>bc2
假
原命题:若四边形对角线相等,则四边形是平行四边形。
假
结 论 4
逆命题和否命题总是同真同假。
否命题与逆命题之间的真假关系
一般的,四种命题的真假性,有且仅有以下四种情况:
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
四种命题的真假性之间的关系:
两个命题互为逆否命题,它们同真同假;
两个命题为互逆或互否命题,它们的真假性没有关系.
四种命题
原命题
逆命题
否命题
逆否命题
真假一致
真假
一致
若 p则 q
若 q则 p
若 p则 q
若 q则 p
课本 第8页 练习
总结
反证法:
要证明某一结论A是正确的,但不直接证明,而是先去证明A的反面(非A)是错误的,从而断定A是正确的。
即反证法就是通过否定命题的结论而导出矛盾来达到肯定命题的结论,完成命题的论证的一种数学证明方法。
反证法的步骤:
假设命题的结论不成立,即假设结论的反面成立。
从这个假设出发,通过推理论证,得出矛盾。
由矛盾判定假设不正确,从而肯定命题的结论正确。
推理过程中一定要用到才行
显而易见的矛盾(如和已知条件矛盾).
可能出现矛盾四种情况:
与题设矛盾;
与反设矛盾;
与公理、定理矛盾;
在证明过程中,推出自相矛盾的结论。
(课本8页B组).证明:圆的两条不是直径的相交弦不能互相平分.
.O
P
A
B
C
D
已知:在⊙O中,弦AB、CD相交于P,且AB、CD不是直径.
求证:弦AB、CD不被P平分
证明:
假设弦AB、CD被P平分,
则P是AB、CD 的中点,
连接OP,
由垂径定理的推论,可得:
OP⊥AB,OP⊥CD.
这与“在平面上过一点有且只有一条直线与已知直线垂直”相矛盾.
∴弦AB、CD不被P平分.
