人教八上数学14.2.1平方差公式 课件(29张ppt)
文档属性
| 名称 | 人教八上数学14.2.1平方差公式 课件(29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 15:05:50 | ||
图片预览








文档简介
(共29张PPT)
§14.2.1
平方差公式
小明同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,小明就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你真是个神童!”小明同学说:“过奖了,我只是利用了在数学上刚学过的一个公式.”
多项式与多项式是如何相乘的?
(a+b)(m+n)
=am
+an
+bm
+bn
①(x
+
4)(
x-4)
②
(6m+
n)(6m-n)
计算下列各题
算一算,比一比,看谁算得又快又准
①(x
+
4)(
x-4)=x2
-
16
x2
-
42
(6m)2
-
n2
(x
+
4)(
x-4)=
(6m+
n)(6m-n)=
②
(6m+
n)(6m-n)=36m2
-
n2
x2
-
42
(x
+
4)(
x-4)=
(6m)2
-
n2
(6m+
n)(6m-n)=
它们的结果有什么特点?
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
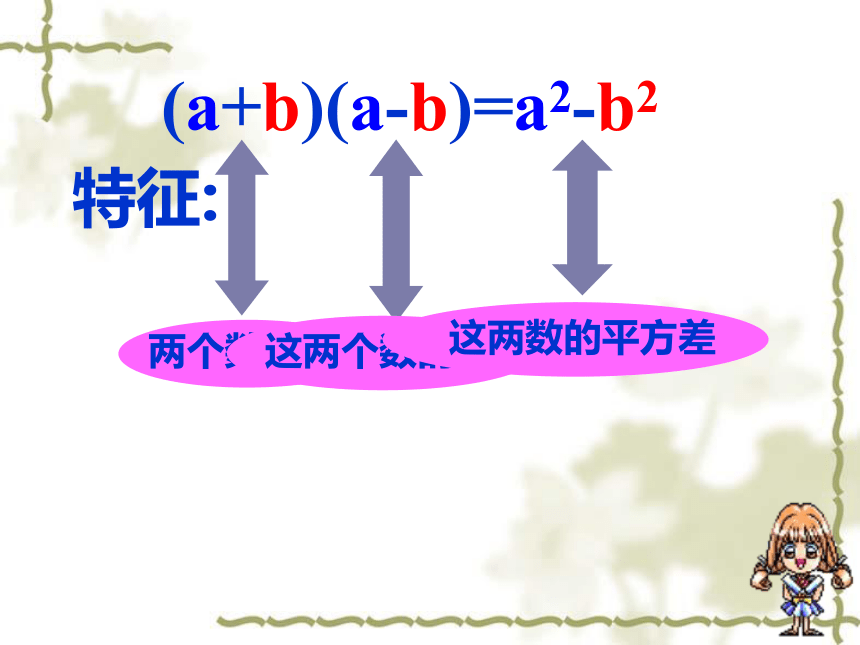
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
两个二项式相乘
(a+b)(a-b)=a2-b2
特征:
相同项
(a+b)(a-b)=a2-b2
特征:
符号相反的项
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(符号相反项)2
(a+b)(a-b)=a2-b2
说明:
公式中字母a、b可以是具体数字,也可以是单项式或多项式。
重点:只要符合公式的结构特征,就可以运用这一公式。
怎样验证?
(a+b)(a-b)
=
a2-b2
(a+b)(a-b)
=
a2-ab+ab-b2
-ab
+ab
=
a2-b2
a2
b2
代数法验证
b
b
a
a
a-b
a-b
a
b
a-b
几何图形验证
(a+b)(a-b)=a2-b2
结论:
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
1、找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(
0.3x)2-12
(a-b)(a+b)
拓
展
练
习
(1)
(a+b)(?a?b)
;
(2)
(a?b)(b?a)
;
(3)
(a+2b)(2b+a);
(4)
?(a?b)(a+b)
;
(5)
(?2x+y)(y?2x).
(不能)
本题是公式的变式训练,以加深对公式本质特征的理解.
下列式子可用平方差公式计算吗?
为什么?
如果能够,怎样计算?
(第一个数不完全一样
)
(不能)
(不能)
(能)
?(a2
?b2)=
?a2
+
b2
;
(不能)
(a
+
b
)
(
a
–
b
)
=
a2
-
b2
例1、用平方差公式计算
计算:(x+2y)(x-2y)
解:原式=
x2
-
(2y)2
=x2
-
4y2
注意
?
1、先把要计算的式子与公式对照,
2、哪个是
a
哪个是
b
例2
运用平方差公式计算:
(1)
(b+2a)(2a-b);
(2)
(-x+2y)(-x-2y).
解:(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
解:
(-x+2y)(-x-2y)
=(-x)2-(2y)2
=
x2-4y2
(a
+
b
)
(
a
–
b
)
=
a2
-
b2
解:
=
=
=100-0.04
=99.96(元).
10.2×9.8
购物问题
例3
计算:
(y+2)
(y-2)
–
(y-1)
(y+5)
.
解:(y+2)(y-2)-
(y-1)(y+5)
=
y2-22-(y2+4y-5)
=
y2-4-y2-4y+5
=
-
4y
+
1.
2、下列计算对不对?如果不对,怎样改正?
2)
错
1)
分析:最后结果应是两项的平方差
错
3)
分析:应先观察是哪两个数的和与这两个数的差
错
分析:应将
当作一个整体,用括号括起来再平方
(1)(a+3b)(a
-
3b)
=4
a2-9;
=(2a+3)(2a-3)
=a2-9b2
;
=(2a)2-32
=(50+1)(50-1)
=502-12
=2500-1
=2499
=(9x2-16)
-(6x2+5x
-6)
=3x2-5x-
10
=(a)2-(3b)2
(2)(3+2a)(-3+2a)
(3)51×49
(5)(3x+4)(3x-4)-(2x+3)(3x-2)
相信自己
我能行!
利用平方差公式计算:
1.计算
20042
-
2003×2005;
拓展提升
解:
20042
-
2003×2005
=
20042
-
(2004-1)(2004+1)
=
20042
-
(20042-12
)
=
20042
-
20042+12
=1
2、利用平方差公式计算:
(a-2)(a+2)(a2
+
4)
解:原式=(a2-4)(a2+4)
=a4-16
1.本节课你有何收获?
2.你还有什么疑问吗?
公式:(a+b)(a-b)=a2-b2
一个
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
公式中的a,b可表示
(1)具体数
(2)单项式
(3)多项式
三个表示
5、思考
(a+b+c)(a+b-c)能用平方差公式运算吗?
若能结果是哪两数的平方差?
www.czsx.com.cn
§14.2.1
平方差公式
小明同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,小明就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你真是个神童!”小明同学说:“过奖了,我只是利用了在数学上刚学过的一个公式.”
多项式与多项式是如何相乘的?
(a+b)(m+n)
=am
+an
+bm
+bn
①(x
+
4)(
x-4)
②
(6m+
n)(6m-n)
计算下列各题
算一算,比一比,看谁算得又快又准
①(x
+
4)(
x-4)=x2
-
16
x2
-
42
(6m)2
-
n2
(x
+
4)(
x-4)=
(6m+
n)(6m-n)=
②
(6m+
n)(6m-n)=36m2
-
n2
x2
-
42
(x
+
4)(
x-4)=
(6m)2
-
n2
(6m+
n)(6m-n)=
它们的结果有什么特点?
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
两个二项式相乘
(a+b)(a-b)=a2-b2
特征:
相同项
(a+b)(a-b)=a2-b2
特征:
符号相反的项
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(符号相反项)2
(a+b)(a-b)=a2-b2
说明:
公式中字母a、b可以是具体数字,也可以是单项式或多项式。
重点:只要符合公式的结构特征,就可以运用这一公式。
怎样验证?
(a+b)(a-b)
=
a2-b2
(a+b)(a-b)
=
a2-ab+ab-b2
-ab
+ab
=
a2-b2
a2
b2
代数法验证
b
b
a
a
a-b
a-b
a
b
a-b
几何图形验证
(a+b)(a-b)=a2-b2
结论:
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
1、找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(
0.3x)2-12
(a-b)(a+b)
拓
展
练
习
(1)
(a+b)(?a?b)
;
(2)
(a?b)(b?a)
;
(3)
(a+2b)(2b+a);
(4)
?(a?b)(a+b)
;
(5)
(?2x+y)(y?2x).
(不能)
本题是公式的变式训练,以加深对公式本质特征的理解.
下列式子可用平方差公式计算吗?
为什么?
如果能够,怎样计算?
(第一个数不完全一样
)
(不能)
(不能)
(能)
?(a2
?b2)=
?a2
+
b2
;
(不能)
(a
+
b
)
(
a
–
b
)
=
a2
-
b2
例1、用平方差公式计算
计算:(x+2y)(x-2y)
解:原式=
x2
-
(2y)2
=x2
-
4y2
注意
?
1、先把要计算的式子与公式对照,
2、哪个是
a
哪个是
b
例2
运用平方差公式计算:
(1)
(b+2a)(2a-b);
(2)
(-x+2y)(-x-2y).
解:(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
解:
(-x+2y)(-x-2y)
=(-x)2-(2y)2
=
x2-4y2
(a
+
b
)
(
a
–
b
)
=
a2
-
b2
解:
=
=
=100-0.04
=99.96(元).
10.2×9.8
购物问题
例3
计算:
(y+2)
(y-2)
–
(y-1)
(y+5)
.
解:(y+2)(y-2)-
(y-1)(y+5)
=
y2-22-(y2+4y-5)
=
y2-4-y2-4y+5
=
-
4y
+
1.
2、下列计算对不对?如果不对,怎样改正?
2)
错
1)
分析:最后结果应是两项的平方差
错
3)
分析:应先观察是哪两个数的和与这两个数的差
错
分析:应将
当作一个整体,用括号括起来再平方
(1)(a+3b)(a
-
3b)
=4
a2-9;
=(2a+3)(2a-3)
=a2-9b2
;
=(2a)2-32
=(50+1)(50-1)
=502-12
=2500-1
=2499
=(9x2-16)
-(6x2+5x
-6)
=3x2-5x-
10
=(a)2-(3b)2
(2)(3+2a)(-3+2a)
(3)51×49
(5)(3x+4)(3x-4)-(2x+3)(3x-2)
相信自己
我能行!
利用平方差公式计算:
1.计算
20042
-
2003×2005;
拓展提升
解:
20042
-
2003×2005
=
20042
-
(2004-1)(2004+1)
=
20042
-
(20042-12
)
=
20042
-
20042+12
=1
2、利用平方差公式计算:
(a-2)(a+2)(a2
+
4)
解:原式=(a2-4)(a2+4)
=a4-16
1.本节课你有何收获?
2.你还有什么疑问吗?
公式:(a+b)(a-b)=a2-b2
一个
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
公式中的a,b可表示
(1)具体数
(2)单项式
(3)多项式
三个表示
5、思考
(a+b+c)(a+b-c)能用平方差公式运算吗?
若能结果是哪两数的平方差?
www.czsx.com.cn
