北师大版八年级数学下册 6.1平行四边形的性质 第1课时 平行四边形边和角的性质 课件(共28张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 6.1平行四边形的性质 第1课时 平行四边形边和角的性质 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 20:06:18 | ||
图片预览





文档简介
6.1 平行四边形的性质
第六章 平行四边形
第1课时 平行四边形边和角的性质
学习目标
1.理解平行四边形的概念;(重点)
2.掌握平行四边形边、角的性质;(重点)
3.利用平行四边形边、角的性质解决问题.(难点)
平行四边形是我们常见的一种图形,它具有十分和谐的对称美.
它是什么样的对称图形呢?它又具有哪些基本性质呢?
情境导入
你还能举出其他的例子吗?
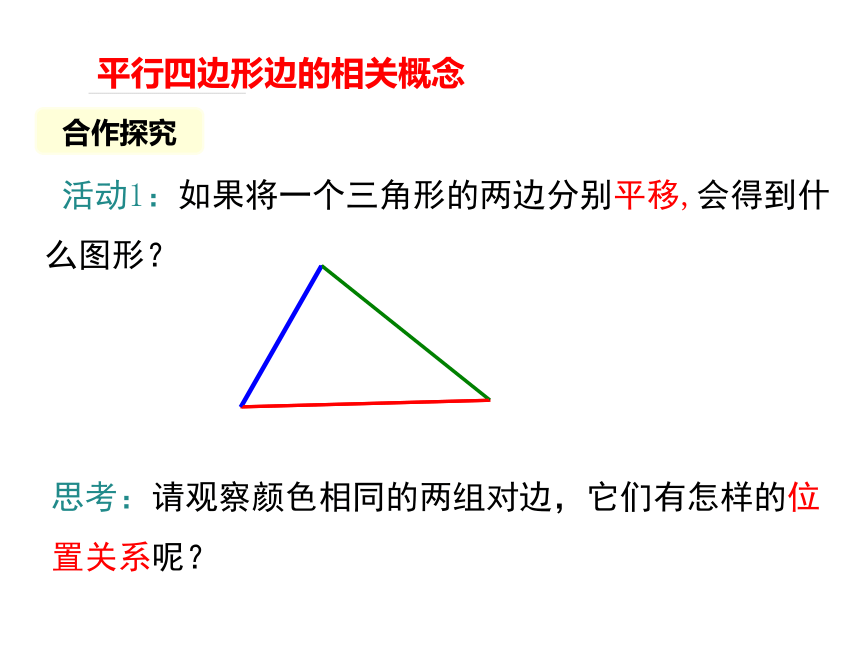
活动1:如果将一个三角形的两边分别平移,会得到什么图形?
思考:请观察颜色相同的两组对边,它们有怎样的位置关系呢?
平行四边形边的相关概念
合作探究
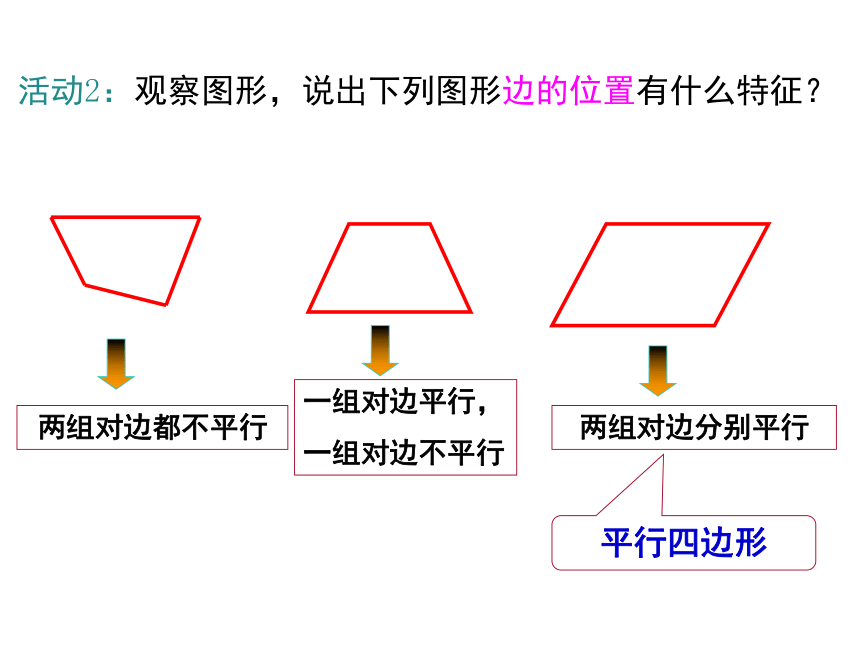
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
平行四边形
活动2:观察图形,说出下列图形边的位置有什么特征?
1.两组对边分别平行的四边形叫做平行四边形.
2.记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,
相对的角称为对角.
概念学习
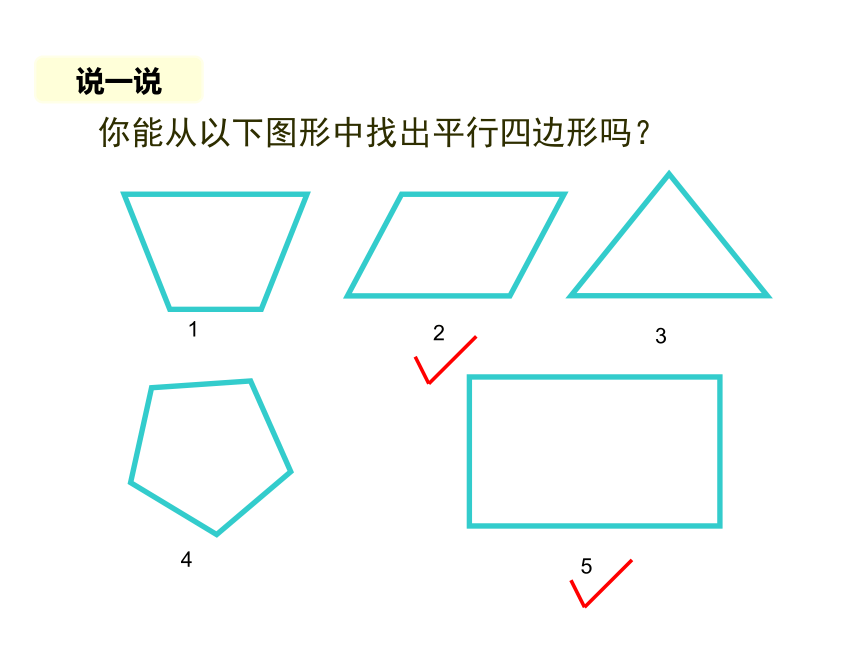
你能从以下图形中找出平行四边形吗?
2
3
1
4
5
说一说
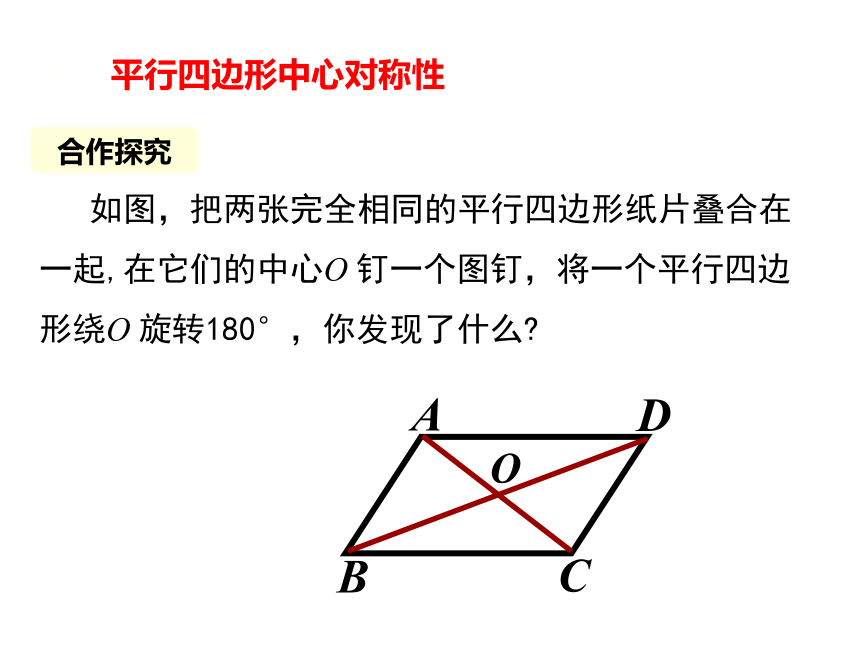
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O 旋转180°,你发现了什么?
A
C
D
B
O
平行四边形中心对称性
一
合作探究
●
A
D
O
C
B
D
B
O
C
A
再看一遍
●
A
D
O
C
B
D
B
O
C
A
你有什么猜想?
根据刚才的旋转,你知道平行四边形是什么图形?
猜一猜
□ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是 中心对称图形,两条对角线的交点O是它的对称中心.
活动3:将两个全等的三角形纸片相等的边重合在一起,你能拼出平行四边形吗?你能拼出几个?与同学交流你的拼法,并把它展示出来.
说一说:通过拼图你可以得到什么启示?
平行四边形对边相等,对角相等.
一
平行四边形边和角的性质
这个结论正确吗?
方法1:度量法
A
B
C
D
这个方法准确吗?
平行四边形的一条对角线把平行四边形分成两个全等的三角形;
A
B
C
D
四边形问题
转化
三角形问题
方法2:推理证明
证明:如图,连接AC.
∵AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA(ASA).
∴AB=CD,AD=CD,
∠B=∠D.
已知: ABCD,AB∥CD,AD∥BC.
求证: AB=CD,BC=DA; ∠B=∠D,∠BAD=∠DCB.
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3,
即∠BAD=∠DCB.
证明结论
思考:不添加辅助线,你能否直接运用平行四边形
的定义,证明其对角相等?
A
B
C
D
证明:∵AB∥DC,
∴∠ABC+∠BCD=180°.
∵AD∥BC,
∴∠BAD+∠ABC=180°.
∴∠BCD=∠BAD.
同理 ∠ABC=∠ADC.
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质
知识要点
性质定理1
性质定理2
例1.已知: ABCD,E,F是对角线AC上的两点,并且AE=CF. 求证: BE=DF.
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF(SAS).
∴ AB=CD,AB ∥ CD.
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
典例精析
例2 有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°,且AE∥BC、AB∥CF. 你能根据测得的数据计算出DE的长度和∠D的度数吗?
解∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=60cm.
∴ED=AD-AE=80-60=20(cm).
答:DE的长度是20cm, ∠D的度数是60°.
A1
A3
A2
A
B
C
练一练:学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
1 .如图,在□ABCD中:
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______.
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
当堂跟踪练习
2.在□ABCD中,∠A=150°,AB=8cm,BC=10cm,
则S□ABCD= .
提示:过点A作AE⊥BC于E,然后利用含30°角的直角三角形的性质求出AE的值.
40cm2
解:在 ABCD中,AB=DC,AD=BC
(平行四边形的对边相等).
∵ AB=8,∴DC=8.
又∵AB+BC+DC+AD=24,
∴AD=BC= (24-2AB)÷2=4.
3.如图,在 ABCD中,AB=8,周长等于24,求其余三条边的长.
B
C
D
A
O
3
-1
2
4.已知点A(3,0)、B(-1,0)、C(0,2),以A、B、C为顶点画平行四边形,你能求出第四个顶点D吗?
O
3
-1
2
(4,2)
(2,-2)
O
3
-1
2
(-4,2)
x
y
x
y
x
y
平行四边形
中心对称图形,两条对角线的交点是它的对称中心
课堂小结
两组对边分别平行的四边形是平行四边形
对称性
定义
性质
对边平行,
对边相等,
对角相等
1.平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的边和角的性质
平行四边形的对边相等,平行四边形的对角相等.
板书设计
学生通过动手操作的过程和观看多媒体课件的演示,得出并掌握平行四边形性质,效果比较好.例题能够引导学生用不同的方法去解决问题并加以变式,能根据学生的具体情况在练习的过程中及时发现问题,并通过投影指出错误,规范说理过程,极大提高课堂效率.
板书设计
第六章 平行四边形
第1课时 平行四边形边和角的性质
学习目标
1.理解平行四边形的概念;(重点)
2.掌握平行四边形边、角的性质;(重点)
3.利用平行四边形边、角的性质解决问题.(难点)
平行四边形是我们常见的一种图形,它具有十分和谐的对称美.
它是什么样的对称图形呢?它又具有哪些基本性质呢?
情境导入
你还能举出其他的例子吗?
活动1:如果将一个三角形的两边分别平移,会得到什么图形?
思考:请观察颜色相同的两组对边,它们有怎样的位置关系呢?
平行四边形边的相关概念
合作探究
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
平行四边形
活动2:观察图形,说出下列图形边的位置有什么特征?
1.两组对边分别平行的四边形叫做平行四边形.
2.记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,
相对的角称为对角.
概念学习
你能从以下图形中找出平行四边形吗?
2
3
1
4
5
说一说
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O 旋转180°,你发现了什么?
A
C
D
B
O
平行四边形中心对称性
一
合作探究
●
A
D
O
C
B
D
B
O
C
A
再看一遍
●
A
D
O
C
B
D
B
O
C
A
你有什么猜想?
根据刚才的旋转,你知道平行四边形是什么图形?
猜一猜
□ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是 中心对称图形,两条对角线的交点O是它的对称中心.
活动3:将两个全等的三角形纸片相等的边重合在一起,你能拼出平行四边形吗?你能拼出几个?与同学交流你的拼法,并把它展示出来.
说一说:通过拼图你可以得到什么启示?
平行四边形对边相等,对角相等.
一
平行四边形边和角的性质
这个结论正确吗?
方法1:度量法
A
B
C
D
这个方法准确吗?
平行四边形的一条对角线把平行四边形分成两个全等的三角形;
A
B
C
D
四边形问题
转化
三角形问题
方法2:推理证明
证明:如图,连接AC.
∵AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA(ASA).
∴AB=CD,AD=CD,
∠B=∠D.
已知: ABCD,AB∥CD,AD∥BC.
求证: AB=CD,BC=DA; ∠B=∠D,∠BAD=∠DCB.
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3,
即∠BAD=∠DCB.
证明结论
思考:不添加辅助线,你能否直接运用平行四边形
的定义,证明其对角相等?
A
B
C
D
证明:∵AB∥DC,
∴∠ABC+∠BCD=180°.
∵AD∥BC,
∴∠BAD+∠ABC=180°.
∴∠BCD=∠BAD.
同理 ∠ABC=∠ADC.
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质
知识要点
性质定理1
性质定理2
例1.已知: ABCD,E,F是对角线AC上的两点,并且AE=CF. 求证: BE=DF.
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF(SAS).
∴ AB=CD,AB ∥ CD.
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
典例精析
例2 有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°,且AE∥BC、AB∥CF. 你能根据测得的数据计算出DE的长度和∠D的度数吗?
解∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=60cm.
∴ED=AD-AE=80-60=20(cm).
答:DE的长度是20cm, ∠D的度数是60°.
A1
A3
A2
A
B
C
练一练:学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
1 .如图,在□ABCD中:
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______.
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
当堂跟踪练习
2.在□ABCD中,∠A=150°,AB=8cm,BC=10cm,
则S□ABCD= .
提示:过点A作AE⊥BC于E,然后利用含30°角的直角三角形的性质求出AE的值.
40cm2
解:在 ABCD中,AB=DC,AD=BC
(平行四边形的对边相等).
∵ AB=8,∴DC=8.
又∵AB+BC+DC+AD=24,
∴AD=BC= (24-2AB)÷2=4.
3.如图,在 ABCD中,AB=8,周长等于24,求其余三条边的长.
B
C
D
A
O
3
-1
2
4.已知点A(3,0)、B(-1,0)、C(0,2),以A、B、C为顶点画平行四边形,你能求出第四个顶点D吗?
O
3
-1
2
(4,2)
(2,-2)
O
3
-1
2
(-4,2)
x
y
x
y
x
y
平行四边形
中心对称图形,两条对角线的交点是它的对称中心
课堂小结
两组对边分别平行的四边形是平行四边形
对称性
定义
性质
对边平行,
对边相等,
对角相等
1.平行四边形的定义
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的边和角的性质
平行四边形的对边相等,平行四边形的对角相等.
板书设计
学生通过动手操作的过程和观看多媒体课件的演示,得出并掌握平行四边形性质,效果比较好.例题能够引导学生用不同的方法去解决问题并加以变式,能根据学生的具体情况在练习的过程中及时发现问题,并通过投影指出错误,规范说理过程,极大提高课堂效率.
板书设计
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
